python实现汉诺塔算法

汉诺塔

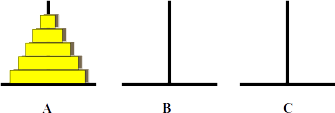
算法分析

1.步骤1：如果是一个盘子，直接将a柱子上的盘子从a移动到c

否则

2.步骤2：先将A柱子上的n-1个盘子借助C移动到B（图1）

已知函数形参为hanoi(n,a,b,c)，这里调用函数的时候是A柱子上的n-1个，A借助C移动到B，所以调用函数hanoi(n-1,a,c,b)

3.步骤3：此时移动完如图1，但是还没有移动结束，首先要将A柱子上最后一个盘子直接移动到C（图2），调用函数hanoi(1,a,b,c)

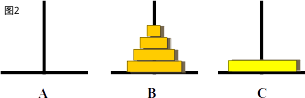
4.步骤4：最后将B柱子上的n-1个盘子借助A移动到C（图3），调用函数hanoi(n-1,b,a,c)

这时递归调用就完成了

代码

def hanoi(n,a,b,c):
    if n == 1:
        print(a,'-->',c)
    else:
        hanoi(n-1,a,c,b)
        hanoi(1,a,b,c)
        hanoi(n-1,b,a,c)

# 测试
hanoi(3,a,b,c)

# A --> C
# A --> B
# C --> B
# A --> C
# B --> A
# B --> C
# A --> C