数据归一化Feature Scaling

当我们有如上样本时，若采用常规算欧拉距离的方法sqrt((5-1)2+(200-100)2), 样本间的距离被‘发现时间’所主导。尽管5是1的5倍，200只是100的2倍。这是由于量纲不同，导致数据不在同一个度量级上。

因此我们需要进行一些数据归一化的处理，将所有的数据映射到同一尺度。

最值归一化：把所有数据映射到0-1之间。

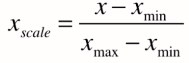
适用于分布有明显边界的情况，缺点是受outlier影响较大。如收入的分布，大多数人是一万，而少部分人月收入是100万。

解决方法出炉(一般都用这种)->

均值方差归一化 standardization: 把所有数据归一到均值为0方差为1的分布中。

数据分布没有明显边界，有可能存在极端数据值时，都可使用这种方法。

（（特征值 - 均值）/ 方差）

数据归一化Feature Scaling的更多相关文章

  1. （一）线性回归与特征归一化(feature scaling)

    线性回归是一种回归分析技术,回归分析本质上就是一个函数估计的问题(函数估计包括参数估计和非参数估计),就是找出因变量和自变量之间的因果关系.回归分析的因变量是应该是连续变量,若因变量为离散变量,则问题 ...

  2. CS229 1 .线性回归与特征归一化(feature scaling)

    线性回归是一种回归分析技术,回归分析本质上就是一个函数估计的问题(函数估计包括参数估计和非参数估计),就是找出因变量和自变量之间的因果关系.回归分析的因变量是应该是连续变量,若因变量为离散变量,则问题 ...

  3. 数据归一化Scaler-机器学习算法

    //2019.08.03下午#机器学习算法的数据归一化(feature scaling)1.数据归一化的必要性:对于机器学习算法的基础训练数据,由于数据类型的不同,其单位及其量纲也是不一样的,而也正是 ...

  4. 第四十九篇 入门机器学习——数据归一化（Feature Scaling）

    No.1. 数据归一化的目的 数据归一化的目的,就是将数据的所有特征都映射到同一尺度上,这样可以避免由于量纲的不同使数据的某些特征形成主导作用.   No.2. 数据归一化的方法 数据归一化的方法主要 ...

  5. Feature Scaling深入理解

    Feature Scaling 可以翻译为特征归一化,或者数据归一化,比如统计学习中,我们一般都会对不同量纲的特征做归一化,深度学习中经常会谈到增加的BN层,LRN层会带来训练收敛速度的提升,等等.问 ...

  6. 机器学习中的特征缩放（feature scaling）

    参考:https://blog.csdn.net/iterate7/article/details/78881562 在运用一些机器学习算法的时候不可避免地要对数据进行特征缩放(feature sca ...

  7. 机器学习：数据归一化（Scaler）

    数据归一化(Feature Scaling) 一.为什么要进行数据归一化 原则:样本的所有特征,在特征空间中,对样本的距离产生的影响是同级的: 问题:特征数字化后,由于取值大小不同,造成特征空间中样本 ...

  8. Feature Scaling

    定义:Feature scaling is a method used to standardize the range of independent variables or features of ...

  9. 浅谈Feature Scaling

    浅谈Feature Scaling 定义:Feature scaling is a method used to standardize the range of independent variab ...

随机推荐

  1. h5-18-文件操作-兼容判断

    <!DOCTYPE html> <html> <head> <meta charset="UTF-8"> <title> ...

  2. windows clone 迁移数据库

    windows clone 迁移数据库可行.(c 盘底成复制)

  3. 507 Perfect Number 完美数

    对于一个 正整数,如果它和除了它自身以外的所有正因子之和相等,我们称它为“完美数”.给定一个 正整数 n, 如果他是完美数,返回 True,否则返回 False示例:输入: 28输出: True解释: ...

  4. freertos之特点

    主要特点:协程(co-routine):任务间的中断通信机制              支持可抢占式/协作式任务调度 .FreeRTOS-MPU              内核对象可以动态或静态分配 ...

  5. 机器学习概念之特征选择（Feature selection）之RFormula算法介绍

    不多说,直接上干货! RFormula算法介绍: RFormula通过R模型公式来选择列.支持R操作中的部分操作,包括‘~’, ‘.’, ‘:’, ‘+’以及‘-‘,基本操作如下: 1. ~分隔目标和 ...

  6. gulp插件之gulp-mock-server

    本文讲gulp-mock-server的应用,用于虚拟一个服务器,模拟后台返回json数据给前端,这样可以一定程度上实现前后端分离,约定好接口之后,前后端即可同时开发,从而提高效率. 在gulpfil ...

  7. js事件、Js中的for循环和事件的关系、this

    一.js事件  1.事件 用户在网页中所触发的行为 鼠标滑动种类很多,键盘.表单特列: 点击:onclick 鼠标进入:onmouseenter 鼠标离开:onmouseleave 鼠标悬浮:onmo ...

  8. 浏览器的差距、ie6 ie7 ie8、符号、html css、BFC、

    1.浏览器的差距 浏览器默认的字体是16px,谷歌的最小字体是12px,其他是10px 2.ie6.ie7.ie8. hack:就是针对不同的浏览器去不同的html,css样式,从而让各个浏览器能达到 ...

  9. http响应头状态描述

    状态代码有三位数字组成,第一个数字定义了响应的类别,且有五种可能取值:1xx:指示信息--表示请求已接收,继续处理2xx:成功--表示请求已被成功接收.理解.接受3xx:重定向--要完成请求必须进行更 ...

  10. 简洁的KVO -- 使用Block响应事件

    涉及内容: KVO,Runtime,Category,Block 首先创建NSObject的Category 举个例子是这样的: 随后定义你需要响应的Block结构 我简单一点就这样咯 typedef ...