codeforces 667D D. World Tour(最短路)

题目链接：

D. World Tour

time limit per test

5 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

A famous sculptor Cicasso goes to a world tour!

Well, it is not actually a world-wide. But not everyone should have the opportunity to see works of sculptor, shouldn't he? Otherwise there will be no any exclusivity. So Cicasso will entirely hold the world tour in his native country — Berland.

Cicasso is very devoted to his work and he wants to be distracted as little as possible. Therefore he will visit only four cities. These cities will be different, so no one could think that he has "favourites". Of course, to save money, he will chose the shortest paths between these cities. But as you have probably guessed, Cicasso is a weird person. Although he doesn't like to organize exhibitions, he likes to travel around the country and enjoy its scenery. So he wants the total distance which he will travel to be as large as possible. However, the sculptor is bad in planning, so he asks you for help.

There are n cities and m one-way roads in Berland. You have to choose four different cities, which Cicasso will visit and also determine the order in which he will visit them. So that the total distance he will travel, if he visits cities in your order, starting from the first city in your list, and ending in the last, choosing each time the shortest route between a pair of cities — will be the largest.

Note that intermediate routes may pass through the cities, which are assigned to the tour, as well as pass twice through the same city. For example, the tour can look like that: 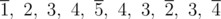. Four cities in the order of visiting marked as overlines:[1, 5, 2, 4].

Note that Berland is a high-tech country. So using nanotechnologies all roads were altered so that they have the same length. For the same reason moving using regular cars is not very popular in the country, and it can happen that there are such pairs of cities, one of which generally can not be reached by car from the other one. However, Cicasso is very conservative and cannot travel without the car. Choose cities so that the sculptor can make the tour using only the automobile. It is guaranteed that it is always possible to do.

Input

 

In the first line there is a pair of integers n and m (4 ≤ n ≤ 3000, 3 ≤ m ≤ 5000) — a number of cities and one-way roads in Berland.

Each of the next m lines contains a pair of integers ui, vi (1 ≤ ui, vi ≤ n) — a one-way road from the city ui to the city vi. Note that uiand vi are not required to be distinct. Moreover, it can be several one-way roads between the same pair of cities.

 

Output

 

Print four integers — numbers of cities which Cicasso will visit according to optimal choice of the route. Numbers of cities should be printed in the order that Cicasso will visit them. If there are multiple solutions, print any of them.

 

Example

 

input

8 9
1 2
2 3
3 4
4 1
4 5
5 6
6 7
7 8
8 5

output

2 1 8 7

Note

Let d(x, y) be the shortest distance between cities x and y. Then in the example d(2, 1) = 3, d(1, 8) = 7, d(8, 7) = 3. The total distance equals 13.

题意：

给一个有向图,选取4个点,使dis[s1][s2]+dis[s2][s3]+dis[s3][s4]最大;

思路：

先找出所有点对之间的最短距离,再暴力枚举s2,s3,对于s1和s4一定是选到s2最远的点和s3能最远到的点

AC代码：

#include <bits/stdc++.h>
using namespace std;
#define Riep(n) for(int i=1;i<=n;i++)
#define Riop(n) for(int i=0;i<n;i++)
#define Rjep(n) for(int j=1;j<=n;j++)
#define Rjop(n) for(int j=0;j<n;j++)
#define mst(ss,b) memset(ss,b,sizeof(b));
typedef long long LL;
const LL mod=1e9+;
const double PI=acos(-1.0);
const int inf=0x3f3f3f3f;
const int N=1e5+;
int n,m;
int p[][],vis[];
vector<int>ve[];
struct node
{
    int num,dis;
};
vector<node>to[],from[];
queue<int>qu;
int bfs(int x)
{
    while(!qu.empty())qu.pop();
    memset(vis,,sizeof(vis));
    qu.push(x);
    vis[x]=;
    while(!qu.empty())
    {
        int fr=qu.front();
        qu.pop();
        vis[fr]=;
        int len=ve[fr].size();
        Riop(len)
        {
            if(p[x][ve[fr][i]]>p[x][fr]+)
            {
                p[x][ve[fr][i]]=p[x][fr]+;
            if(!vis[ve[fr][i]])
            {
                vis[ve[fr][i]]=;
                qu.push(ve[fr][i]);
            }
            }
        }
    }
}
int cmp(node x,node y)
{
    return x.dis>y.dis;
}
int main()
{
    scanf("%d%d",&n,&m);
    Riep(n)
        Rjep(n)
        if(i!=j)p[i][j]=inf;
        else p[i][j]=;
    int u,v;
    Riep(m)
    {
        scanf("%d%d",&u,&v);
        ve[u].push_back(v);
    }
    Riep(n)bfs(i);
    node x;
    Riep(n)
    {
        Rjep(n)
        {
            if(p[i][j]!=inf&&i!=j)
            {
                x.num=i,x.dis=p[i][j];
                to[j].push_back(x);
                x.num=j;
                from[i].push_back(x);
            }
        }
    }

    Riep(n)sort(to[i].begin(),to[i].end(),cmp),sort(from[i].begin(),from[i].end(),cmp);
    int dis=,ans1,ans2,ans3,ans4,s1,s2,s3,s4;
    Riep(n)
    {
        s2=i;
        Rjep(n)
        {
            s3=j;
            if(i==j||p[i][j]==inf)continue;
            for(int k=;k<&&k<to[i].size();k++)
            {
                if(i==to[i][k].num||j==to[i][k].num)continue;
                s1=to[i][k].num;
                for(int d=;d<&&d<from[j].size();d++)
                {
                    if(i==from[j][d].num||j==from[j][d].num||s1==from[j][d].num)continue;
                    s4=from[j][d].num;
                    if(p[s1][s2]+p[s2][s3]+p[s3][s4]>dis)
                    {
                        dis=p[s1][s2]+p[s2][s3]+p[s3][s4];
                        ans1=s1,ans2=s2,ans3=s3,ans4=s4;
                    }
                }
            }
        }
    }
    printf("%d %d %d %d\n",ans1,ans2,ans3,ans4);

    return ;
}