集成学习_Bagging 和随机森林（rf）

   集成学习方式总共有3种：bagging-(RF)、boosting-(GBDT/Adaboost/XGBOOST)、stacking

     下面将对Bagging 进行介绍：（如下图所示）

     用Bagging的方法抽取训练集时，大约有1/3 的数据没有被抽到。

   

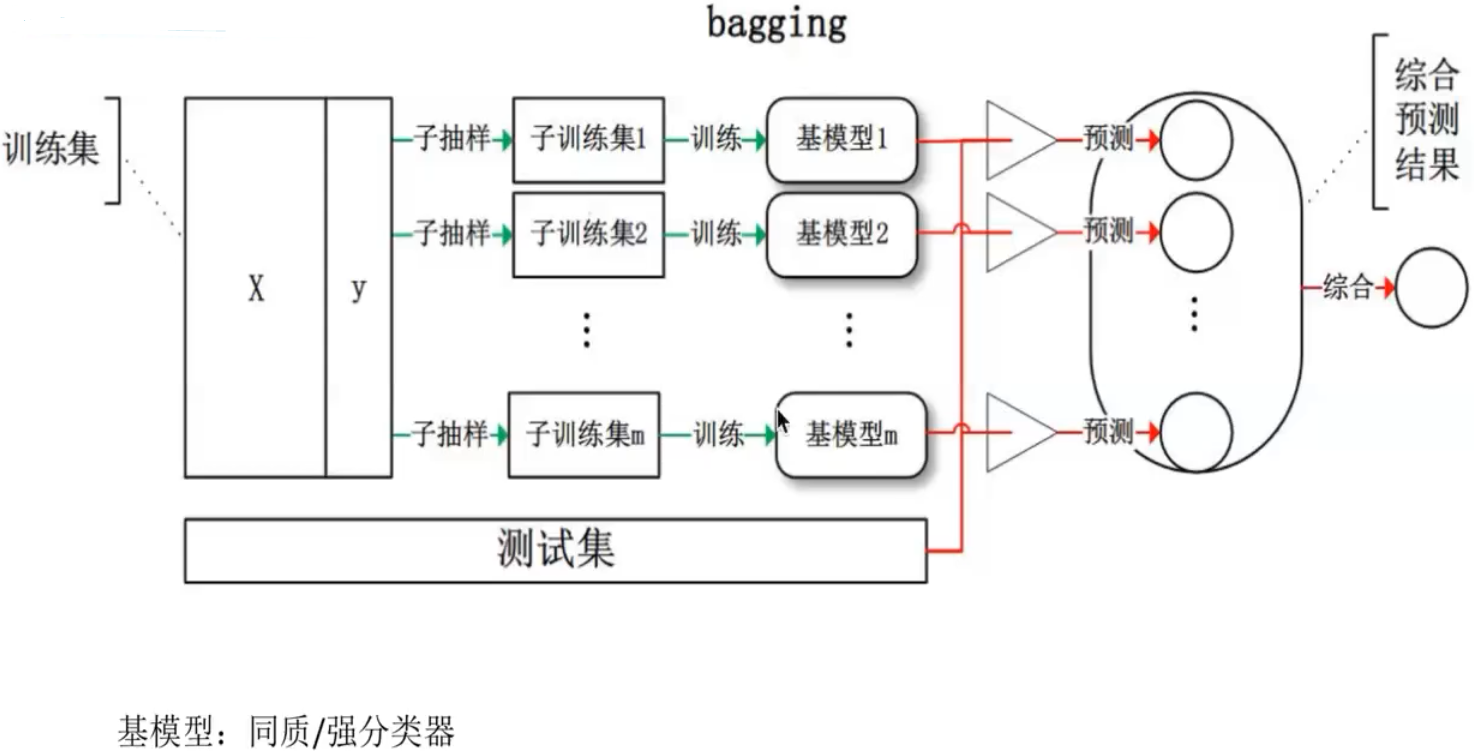
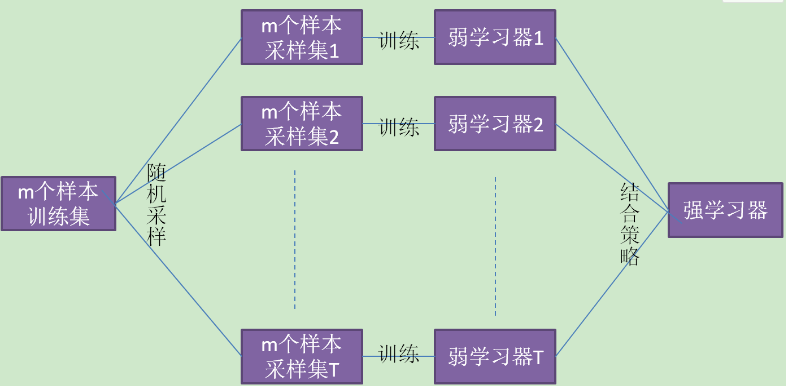
       从训练集进行一系列的子抽样，得到子训练集，训练成基模型，测试集被用来在整个基模型上进行预测，得到的综合预测结果。（看上面右边的图增加理解）

       bagging 怎么避免过拟合，其是通过多个基模型求平均 ，就相当于避免过拟合。

随机森林是它是Bagging算法的进化版。

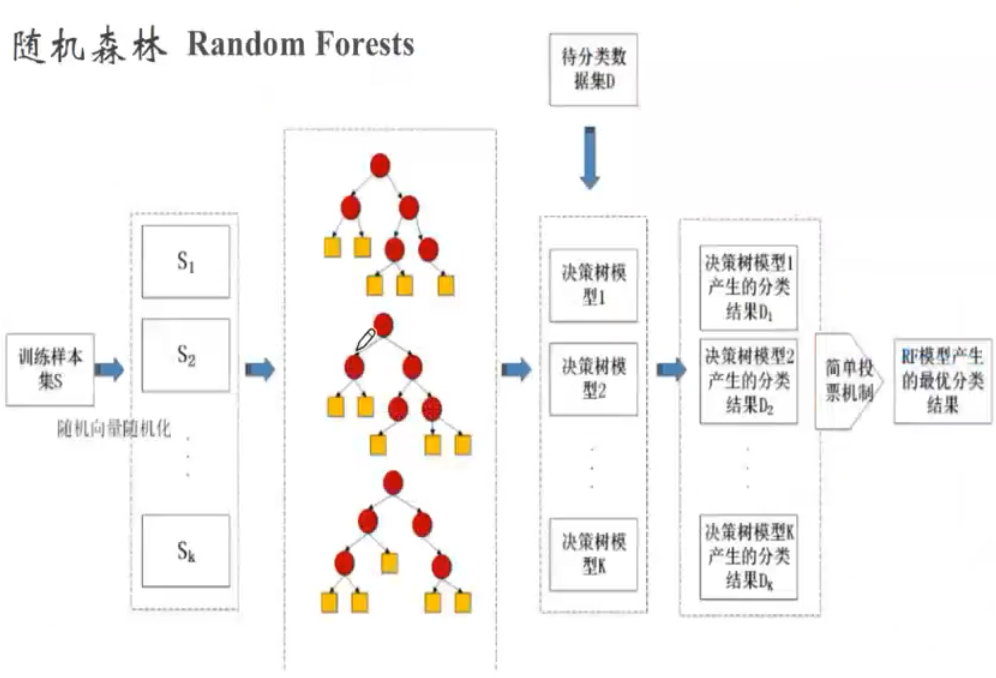
随机森林的思想仍然是bagging,但是进行了独有的改进。

(1) RF使用了CART决策树作为弱学习器。

(2)在使用决策树的基础上，RF对决策树的建立做了改进,对于普通的决策树，我们会在节点上所有的n个样本特征中选择一个最优的特征来做决策树的左右子树划分，但是RF通过随机选择节点上的一部分样本特征，这个数字小于n，假设为n_sub，然后在这些随机选择的n_sub个样本特征中，选择一个最优的特征来做决策树的左右子树划分.这样进一步增强了模型的泛化能力。

n_sub 越小，则模型约健壮，当然此时对于训练集的拟合程度会变差.也就是说n_sub越小，模型的方差会减小,但是偏倚会增大。在实际案例中，一般会通过交叉验证调参获取一个合适的n_sub的值。