KNN-K近邻算法(1)

KNN(K-nearest neighbors)

• 思想简单
• 数学所需知识少（近零）
• 效果好
• 可解释机器学习算法使用过程中的很多细节问题
• 更完整的刻画机器学习应用的流程
• 天然可解决多分类问题
• 可解决回归问题

K近邻本质：如果两个样本足够相似，那么它们就有可能属于同一类别。

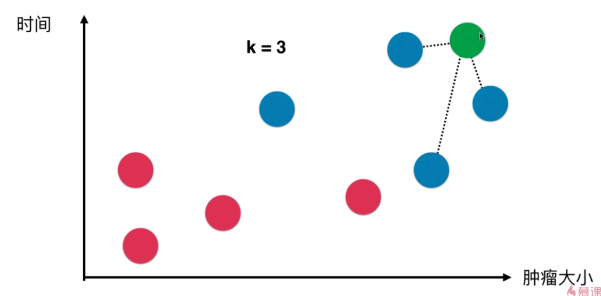
e.g. 绿色的点是新加入的点，取其最近的k（3）个点作为小团体来投票，票数高的获胜（蓝比红-3：0）,所以绿点应该也是蓝点

计算距离：

最常见 -> 欧拉距离，求a, b两点的距离（二维，三维，多维）：

 -> 

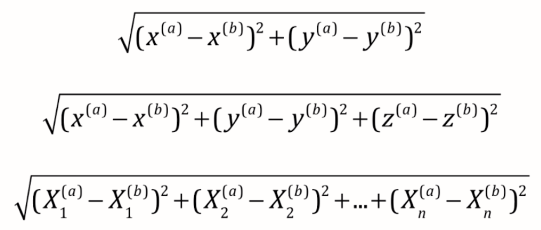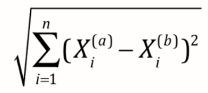
理解小笔记：(（a样本第一个维度特征-b样本第一个维度特征）² + （a样本第二个维度特征-b样本第二个维度特征）² + ... ) 再开根

近乎可以说，KNN算法是机器学习中唯一一个不需要训练过程的算法。输入用例可直接送给训练数据集。

• KNN可以被认为是没有模型的算法
• 为和其他算法统一，可认为其训练数据集本身就是模型

使用KNN解决回归问题

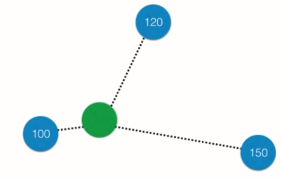
绿点的值即可设为离它最近的三个点的（加权）平均值

KNN缺点

最大缺点：效率低下。

如果训练集有m个样本，n个特征，则预测每一个新的数据，都需要计算它与每一个点之间的距离(共m个点)，每计算一个点的距离就需要O(n)的时间复杂度。

每预测一个，共需要O(m*n)的时间复杂度。

优化，使用树的结构：KD-Tree， Ball-Tree

缺点2：高度数据相关

尽管所有的机器学习算法都是根据给定的数据集来学习，都是高度数据相关的。但KNN相对而言对outlier更加敏感。例如加入使用k=3，当预测点旁有两个错误数据就足以导致预测结果的错误。

缺点3：预测结果不具有可解释性

往往实际应用中我们只知道结果是什么是不够的，我们需要知道为什么是这样的结果从而得到某种规律可以进行推广。

缺点4：维数灾难

随维度的增加，“看似相近”的两个点之间的距离越来越大

解决方法：降维

超参数

指在算法运行前需要决定的参数。

与之相对的模型参数指：算法过程中学习的参数。

KNN算法中没有模型参数，其中K是典型的超参数。

寻找好的超参数：

• 领域知识
• 经验数值
• 实验搜索：尝试测试几组不同的超参数，找到最好的配对

KNN中的其他超参数？ -> 距离权重

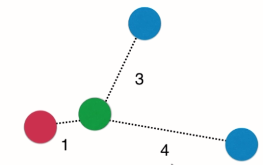
权重一般取距离的倒数。

考虑距离权重的另一个好处：可解决平票问题

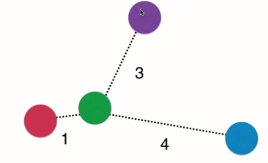
不考虑距离时，红蓝紫平票，模型会随机选一个颜色作为输出结果。但很明显这是不合理的（滑稽脸）。而加入距离权重后，则小红获胜（合情合理有理有据）。

更多的距离定义

之前说到的距离都是欧拉距离。还有一种常见的距离叫曼哈顿距离。

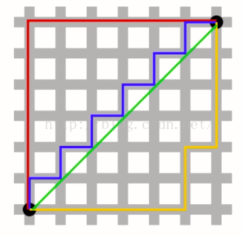
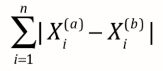
定义为：两点在每个维度上距离的和。如上图例子中黑色两点的曼哈顿距离即它两在x方向上的差值加上y方向上的差值。所有彩线的曼哈顿距离都相同（其中绿线即欧拉距离）

推广一下可发现：

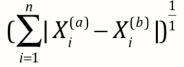  -> 曼哈顿距离

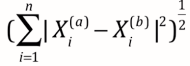 -> 欧拉距离

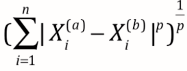 -> 明可夫斯基距离Minkowski distance

当p=1时，明可是曼哈顿距离，p=2时，变身成曼哈顿距离，p=其他数，其他距离的表示方式。

【系统提示】叮咚！又获得一个新的超参数，p

由sklearn中叫metric的超参数控制，默认为明可夫斯基距离

• 向量空间余弦相似度 Cosine Similarity
• 调整余弦相似度 Adjusted Cosine Similarity
• 皮尔森相关系数 Pearson Correlation Coefficient
• Jaccard相似系数 Jaccard Coefficient