14-敌兵布阵（HDU1166线段树 & 树状数组）

http://acm.hdu.edu.cn/showproblem.php?pid=1166

　　　　　　　　　　　　　　　　敌兵布阵

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 107225    Accepted Submission(s): 45072

Problem Description

C国的死对头A国这段时间正在进行军事演习，所以C国间谍头子Derek和他手下Tidy又开始忙乎了。A国在海岸线沿直线布置了N个工兵营地,Derek和Tidy的任务就是要监视这些工兵营地的活动情况。由于采取了某种先进的监测手段，所以每个工兵营地的人数C国都掌握的一清二楚,每个工兵营地的人数都有可能发生变动，可能增加或减少若干人手,但这些都逃不过C国的监视。
中央情报局要研究敌人究竟演习什么战术,所以Tidy要随时向Derek汇报某一段连续的工兵营地一共有多少人,例如Derek问:“Tidy,马上汇报第3个营地到第10个营地共有多少人!”Tidy就要马上开始计算这一段的总人数并汇报。但敌兵营地的人数经常变动，而Derek每次询问的段都不一样，所以Tidy不得不每次都一个一个营地的去数，很快就精疲力尽了，Derek对Tidy的计算速度越来越不满:"你个死肥仔，算得这么慢，我炒你鱿鱼!”Tidy想：“你自己来算算看，这可真是一项累人的工作!我恨不得你炒我鱿鱼呢!”无奈之下，Tidy只好打电话向计算机专家Windbreaker求救,Windbreaker说：“死肥仔，叫你平时做多点acm题和看多点算法书，现在尝到苦果了吧!”Tidy说："我知错了。。。"但Windbreaker已经挂掉电话了。Tidy很苦恼，这么算他真的会崩溃的，聪明的读者，你能写个程序帮他完成这项工作吗？不过如果你的程序效率不够高的话，Tidy还是会受到Derek的责骂的.

 

Input

第一行一个整数T，表示有T组数据。
每组数据第一行一个正整数N（N<=50000）,表示敌人有N个工兵营地，接下来有N个正整数,第i个正整数ai代表第i个工兵营地里开始时有ai个人（1<=ai<=50）。
接下来每行有一条命令，命令有4种形式：
(1) Add i j,i和j为正整数,表示第i个营地增加j个人（j不超过30）
(2)Sub i j ,i和j为正整数,表示第i个营地减少j个人（j不超过30）;
(3)Query i j ,i和j为正整数,i<=j，表示询问第i到第j个营地的总人数;
(4)End 表示结束，这条命令在每组数据最后出现;
每组数据最多有40000条命令

 

Output

对第i组数据,首先输出“Case i:”和回车,
对于每个Query询问，输出一个整数并回车,表示询问的段中的总人数,这个数保持在int以内。

 

Sample Input

1
10
1 2 3 4 5 6 7 8 9 10
Query 1 3
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End

 

Sample Output

Case 1:
6
33
59

 

Author

Windbreaker

 

Recommend

Eddy   |   We have carefully selected several similar problems for you:  1394 1698 1754 1542 1540

 

 方法一：线段树：

讲解：https://www.nowcoder.com/live/153/12/1

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int ans;
const int N = 1e5 + 10;
struct setTree{
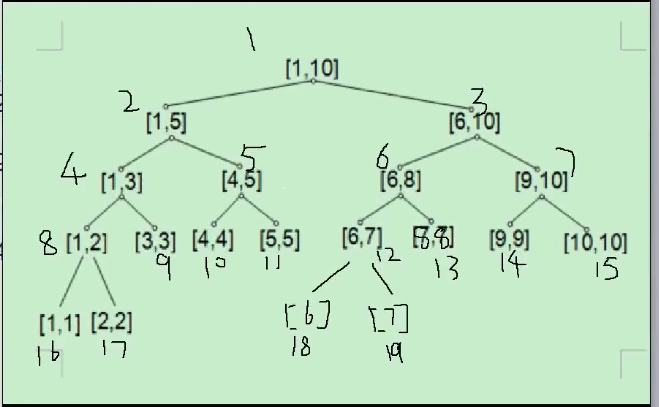
	int l, r;  //l,r为左右区间值
	int v;     //节点存储的值，本题中是两个儿子节点的值之和（其他题目中可以是最大值）
}T[4*N];

void build(int l, int r, int k){  //建树 ，节点编号为k
	T[k].l = l, T[k].r = r;
	if(l == r){
		scanf("%d", &T[k].v);
		return ;
	}
	int mid = (l + r) / 2;
	build(l, mid, k * 2);
	build(mid + 1, r, k * 2 + 1);
	T[k].v = T[k * 2].v + T[k * 2 + 1].v;
}

void update(int c, int v, int k){ //表示将第u个数加上v,当前遍历的节点编号为k
	if(T[k].l == T[k].r && T[k].l == c){
		T[k].v += v;
		return ;
	}
	int mid = (T[k].l + T[k].r) / 2;
	if(c <= mid) //mid在前一半
		update(c, v, k * 2);
	else
		update(c, v, k * 2 + 1);
	T[k].v = T[k * 2].v + T[k * 2 + 1].v;
}

void query(int l, int r, int k){
	if(l > T[k].r || r < T[k].l){
		return ;
	}
	if(l <= T[k].l && r >= T[k].r){
		ans += T[k].v;
		return ;
	}
	int mid = (T[k].l + T[k].r) / 2;
	if(r < mid){
		query(l, r, k * 2);
	}
	else if(l > mid){
		query(l, r, k * 2 + 1);
	}
	else{
		query(l, mid, k * 2);
		query(mid + 1, r, k * 2 + 1);
	}
}

int main(){
	int t, n, p = 0;
	cin >> t;
	while(t--){
		cin >> n;
		build(1, n, 1);
		char op[10];
		printf("Case %d:\n", ++p);
		while(scanf("%s", op), op[0] != 'E'){
			int u, v;
			scanf("%d%d", &u, &v);
			if(op[0] == 'A'){       //add表示将第u个数加上v
				update(u, v, 1);
			}
			else if(op[0] == 'S'){ 	//减即为加上负数
				update(u, -v, 1);
			}
			else{                   //求和
				ans = 0;
				query(u, v, 1);
				printf("%d\n", ans);
			}
		}
	}

	return 0;
}

　　方法二：树状数组：视屏讲解：https://www.nowcoder.com/study/live/153/11/1

　　树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为
log(n)的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修
改一个元素的值。

例如：13
  (2^0 = 1)          13
1101 -- 1101
1100   (2^2 = 4)         12
1001 -- 1100
1000   (2^ 3 = 8)         8
0001 -- 1000

每次减去末尾的1；

Lowbit操作
X & (-X)
12
1100
0100 &
---------
0100

（ps: 原码即为普通化为的二进制，反码即为原码按位取反，补码为反码加一：如 8：0100, 1011,1100）

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
int sum[50005];  //sum[x]表示的是区间为2^k个元素的和，k为x的二进制末尾0的个数，以为最后一个元素为a[x],
int n;			 //所以sum[x] = a[n - 2^k + 1] + ...+ a[x]; 看图理解	

void update(int pos, int val){
	while(pos <= n){  //一直更新到最后
		sum[pos] += val;
		pos += (pos & (-pos));  //pos && (-pos)找到pos二进制末尾第一个1
	}
}

int query(int pos){
	int ans = 0;
	while(pos > 0){   //一直加到0
		ans += sum[pos];
		pos -= (pos & (-pos));
	}
	return ans;
}

int main(){
	int t, icase = 0;
	scanf("%d", &t);
	while(t--){
		memset(sum, 0, sizeof(sum));
		int x;
		scanf("%d", &n);
		for(int i = 1; i <= n; i++){
			scanf("%d", &x);
			update(i, x);
		}
		printf("Case %d:\n", ++icase);
		char ch[10];
		while(scanf("%s", ch), ch[0] != 'E'){
			int u, v;
			scanf("%d%d", &u, &v);
			if(ch[0] == 'A'){
				update(u, v);
			}
			else if(ch[0] == 'S'){
				update(u, -v);
			}
			else{
				printf("%d\n", query(v) - query(u - 1));
			}
		}
	}

	return 0;
}