POJ2528 Mayor's posters（线段树染色问题+离散化）

题目大意：有t组数据，每组数据给你n张海报（1<=n<=10000）,下面n组数据分别给出每张海报的左右范围（1 <= l <= r <= 10000000），下一张海报会覆盖前一张海报，求最后可见（包括完全和不完全可见）的海报有几张。

例如：

1
5
1 4
2 6
8 10
3 4
7 10

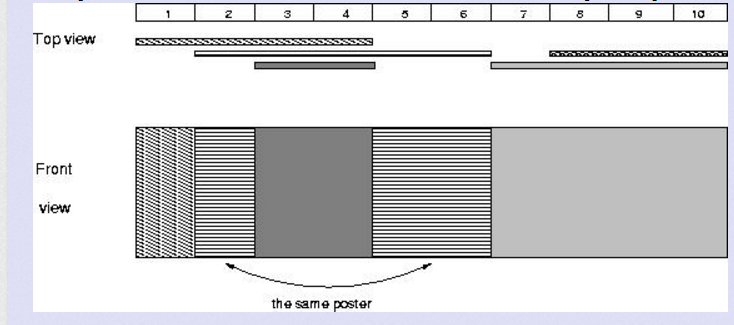
如上图所示，答案为4。

解题思路：其实这是一道区间染色问题，但是由于查找区间太大，显然直接建树会导致MLE，所以这里通过使用对区间的离散化来缩小查找范围。参考了一些大牛博客，简单说一下。

通俗点说，离散化就是压缩区间，使原有的长区间映射到新的短区间，但是区间压缩前后的覆盖关系不变。举个例子：

有一条1到10的数轴（长度为9），给定4个区间[2,4] [3,6] [8,10] [6,9]。现在我们抽取这4个区间的8个端点，2 4 3 6 8 10 6 9。删除相同点并对其升序排序，得2 3 4 6 8 9 10

然后建立映射

2     3     4     6     8     9   10

↓     ↓      ↓     ↓     ↓     ↓     ↓

1     2     3     4     5     6     7

那么新的4个区间为 [1,3] [2,4] [5,7] [4,6]，覆盖关系没有被改变。新数轴为1到7，即原数轴的长度从9压缩到6。

但是对于这道题目来说，这样简单的离散化是不行的，比如三张海报为：1~10、1~4、7~10，就有区间[1,10],[1,4],[7,10]。

按照上述方法离散化后的到区间[1,4],[1,2],[3,4]。答案为2，实际上答案为3。

因为上述做法忽略了区间[2,3]的存在，也就是原来的5~6这一块。

新的离散方法为：在相差大于1的数间加一个数(我选择加入两个数的中间值)，这样的含义是用一个数字来表示其中间的那块区间，解决某块区间被忽略的问题。

例如在上面1 4 6 10中,

X[ 1 ] = 1, X[ 2 ]=2,X[ 3 ] = 4,X[ 4 ] = 5, X[ 5 ] = 7，X[ 6 ]=8, X[ 7 ] = 10

这样之后，第一次是1~7被染成1；第二次1~3被染成2；第三次5~7被染成3

最终，1~3为2，4为1，5~7为3，于是输出正确结果3。

代码：

 #include<iostream>
 #include<cstring>
 #include<algorithm>
 #define LC(a) ((a<<1))
 #define RC(a) ((a<<1)+1)
 #define MID(a,b) ((a+b)>>1)
 using namespace std;
 typedef long long ll;
 const int N=5e4*;

 struct node{
     ll l,r;
     ll color;//颜色为-1表示混合色
 }tree[N];

 struct knode{
     ll l,r;//用来存储题目给定的区间
 }tmp[N];

 ll ans[N];//记录颜色i是否存在
 ll Hash[N];//存储坐标映射
 ll point[N];//存储坐标序列
 //下推
 void pushdown(ll p){
     tree[RC(p)].color=tree[LC(p)].color=tree[p].color;
 }
 //上推
 void pushup(ll p){
     tree[p].color=(tree[LC(p)].color==tree[RC(p)].color?tree[LC(p)].color:-);
 }

 void build(ll p,ll l,ll r){
     tree[p].l=l;
     tree[p].r=r;
     tree[p].color=;
     if(l==r){
         return;
     }
     build(LC(p),l,MID(l,r));
     build(RC(p),MID(l,r)+,r);
 }

 void update(ll p,ll l,ll r,ll color){
     if(r<tree[p].l||l>tree[p].r)
         return;
     if(l<=tree[p].l&&r>=tree[p].r){
         tree[p].color=color;
         return;
     }
     //**释放lazy标记
     if(tree[p].color!=-){
         pushdown(p);
     }
     update(LC(p),l,r,color);
     update(RC(p),l,r,color);
     pushup(p);
 }

 void query(ll p,ll l,ll r){
     if(r<tree[p].l||l>tree[p].r)
         return;
     //纯色，不用再找下去
     if(tree[p].color!=-){
         ans[tree[p].color]=;
         return;
     }
     query(LC(p),l,r);
     query(RC(p),l,r);
 }

 //二分查找
 ll Bin_search(ll l,ll r,ll x){
     ll mid;
     while(l<=r){
         mid=(l+r)/;
         if(x==Hash[mid])    return mid;
         if(x<Hash[mid])     r=mid-;
         else if(x>Hash[mid])    l=mid+;
     }
     return -;
 }

 int main(){
     ios::sync_with_stdio(false);
     ll t,n;
     cin>>t;
     while(t--){
         cin>>n;
         //***对输入数据进行离散化
         ll m1=;

         for(int i=;i<=n;i++){
             ll l,r;
             cin>>tmp[i].l>>tmp[i].r;
             point[++m1]=tmp[i].l;
             point[++m1]=tmp[i].r;
         }
         sort(point+,point++m1);
         ll m2=;
         for(int i=;i<=m1;i++){
             if(point[i]!=point[i-]){
                 if(point[i]-point[i-]>&&i!=){
                     Hash[++m2]=(point[i]+point[i-])>>;
                     Hash[++m2]=point[i];
                 }
                 else
                     Hash[++m2]=point[i];
             }
         }
         //**建树
         build(,,m2);
         for(int i=;i<=n;i++){
             ll l=Bin_search(,m2,tmp[i].l);
             ll r=Bin_search(,m2,tmp[i].r);
             update(,l,r,i);
         }
         memset(ans,,sizeof(ans));
         query(,,m2);
         ll cnt=;
         for(int i=;i<=m2;i++){
             if(ans[i]){
                 cnt++;
             }
         }
         cout<<cnt<<endl;
     }
 }