平衡二叉树（AVL）的实现，附可运行C语言代码
最近几月一直在自学C语言和数据结构，先是写了排序二叉树，觉得平衡二叉树作为一个经典数据结构，有必要实现一下。
网上看了些资料，在AVL和红黑树之间考虑，最后个人还是倾向于AVL。
不同于标准AVL的是，笔者没有使用平衡因子，直接根据左右孩子的高度差值判断是否平衡。整个平衡二叉树是在普通二叉查找树的基础上修改得到的，对于学习数据结构的同学来说，这样逐步提高难度，写起来挑战性没那么大。
代码经测试是可以运行，并实现插入、删除、修改节点时都可以保持平衡。相对于普通二叉查找树，AVL在查找时效率高耗时短，但为了保持高度平衡，必须牺牲插入和删除操作的复杂度。本文将分步讲解如何编写平衡二叉树，全文最后附有完整代码。
当左右子树的高度差超过1时（即≥2，在实际处理时，等于2即为不平衡，进行调整操作，所以不会出现大于2的情况），整棵树失去平衡。写代码之前先了解AVL是如何使二叉树保持平衡，这里涉及到对节点的旋转操作，分四种情况，左左，右右，左右，右左。下面分别解释：
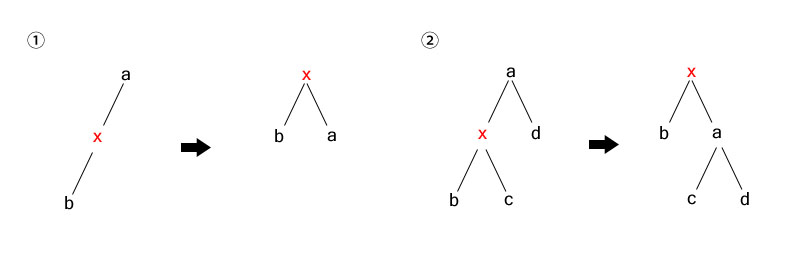
一、左左单旋转
在节点x的左孩子插入节点b
①x无右孩子，旋转节点a即可达到平衡
②x有右孩子c，旋转节点a后，根据a>c>x，需将节点c移动到a的左子树
函数代码如下：
static BTNode *singleRotateLL(BTree *BT, BTNode *phead)
{//不平衡情况为左左的单旋转操作
BTNode *temp; if(phead == NULL)
return ; temp = phead->lchild; if(temp->rchild != NULL){
phead->lchild = temp->rchild;
phead->lchild->height = tree_node_height(BT, phead->lchild);
}
else
phead->lchild = NULL; temp->rchild = phead;
if(temp->rchild->data == BT->phead->data){
BT->phead = temp;
}
phead = temp;
temp->rchild->height = tree_node_height(BT, temp->rchild);
temp->height = tree_node_height(BT, temp);
phead->height = tree_node_height(BT, phead); return phead;
}
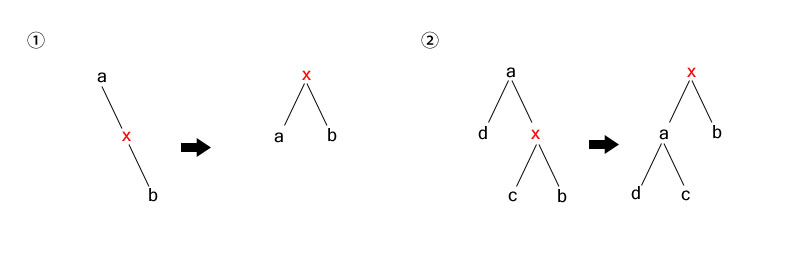
二、右右单旋转
在节点x的右孩子插入节点b
①x无左孩子，旋转节点a即可达到平衡
②x有左孩子c，旋转节点a后，根据x>c>a，需将节点c移动到a的右子树
函数代码如下：
static BTNode *singleRotateRR(BTree *BT, BTNode *phead)
{//不平衡情况为右右的单旋转操作
BTNode *temp; if(phead == NULL)
return ; temp = phead->rchild; if(temp->lchild != NULL){
phead->rchild = temp->lchild;
phead->rchild->height = tree_node_height(BT, phead->rchild);
}
else
phead->rchild = NULL; temp->lchild = phead;
if(temp->lchild->data == BT->phead->data){
BT->phead = temp;
}
phead = temp;
temp->lchild->height = tree_node_height(BT, temp->lchild);
temp->height = tree_node_height(BT, temp);
phead->height = tree_node_height(BT, phead); return phead;
}
注：需要注意的是节点旋转后，节点赋值和高度的更新，初学者很容易忽略或是弄错赋值顺序
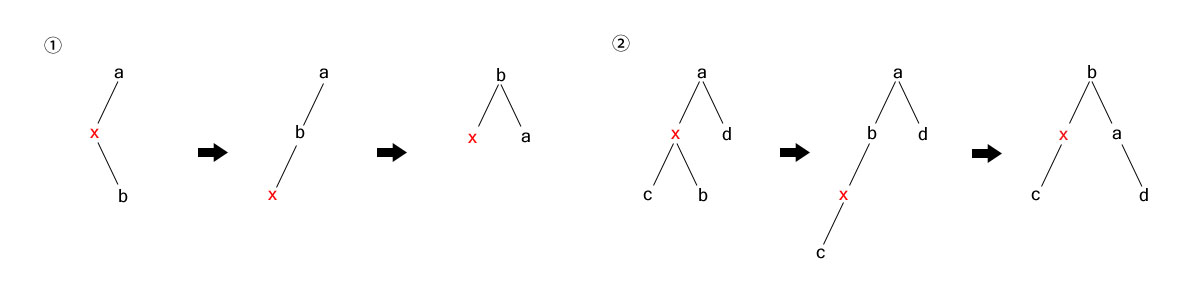
三、左右双旋转
在节点x的右孩子插入节点b
①x无左孩子，②x有左孩子c，这两种情况的处理相同，首先对x节点进行右右单旋转操作，然后对a节点进行左左单旋转操作
函数代码如下：
static BTNode *doubleRotateLR(BTree *BT, BTNode *phead)
{//不平衡情况为左右的双旋转操作
BTNode *temp; if(phead == NULL)
return ; temp = phead->lchild;
phead->lchild = singleRotateRR(BT, temp);
temp = phead;
phead = singleRotateLL(BT, temp); return phead;
}
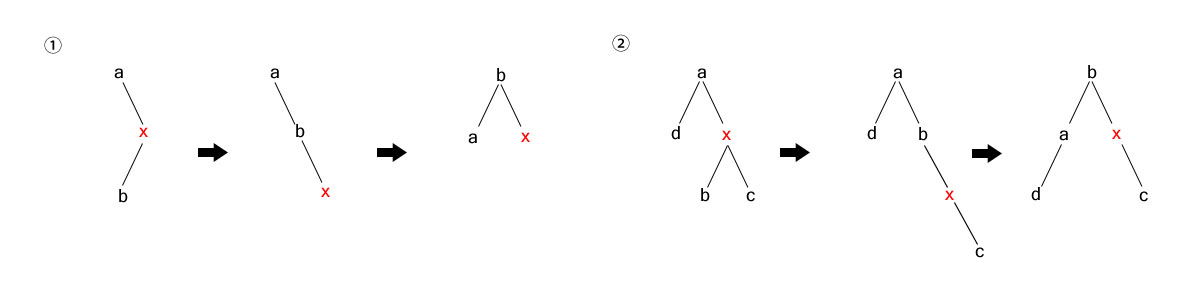
四、右左双旋转
在节点x的右孩子插入节点b
①x无右孩子，②x有右孩子c，这两种情况的处理相同，首先对x节点进行左左单旋转操作，然后对a节点进行右右单旋转操作
函数代码如下：
static BTNode *doubleRotateRL(BTree *BT, BTNode *phead)
{//不平衡情况为右左的双旋转操作
BTNode *temp; if(phead == NULL)
return ; temp = phead->rchild;
phead->rchild = singleRotateLL(BT, temp);
temp = phead;
phead = singleRotateRR(BT, temp); return phead;
}
弄清楚了怎样通过旋转达到平衡状态，接下来一步一步构造平衡二叉树。
第一步，我们要在二叉树的节点中加一个属性：高度，在后面的插入和删除函数中将会用到。
结构体代码如下：
typedef struct _BTNode{
TYPE data;
int height;
struct _BTNode *lchild;
struct _BTNode *rchild;
}BTNode;
第二步，需要添加三个辅助函数，一是求节点的高度，而是遍历求树中每个节点的高度（在删除函数中会用到），三是求两个高度的最大值。
static int tree_node_height(BTree *BT, BTNode *phead)
{//求节点的高度，写成函数解决指针为空的情况，默认空节点的高度为-1，只有一个根节点的节点的高度为0，每多一层高度加1
if(phead != NULL){
if(phead->lchild == NULL && phead->rchild == NULL){
return ;
}
else{
return phead->height = max_height(tree_node_height(BT, phead->lchild), tree_node_height(BT, phead->rchild)) + ;
}
}
else{
return -;
}
} static void tree_height(BTree *BT, BTNode *phead)
{//遍历求树中每个节点的高度
if(phead == NULL)
return; tree_node_height(BT, phead);
if(phead->lchild != NULL)
tree_node_height(BT, phead->lchild);
if(phead->rchild != NULL)
tree_node_height(BT, phead->rchild);
} static int max_height(int height1, int height2)
{//求两个高度的最大值
if(height1 > height2)
return height1;
else
return height2;
}
第三步，插入
插入操作与二叉查找树的操作基本相同，只是在插入后需判断是否平衡，如果不平衡，进行旋转调整。因为BTNode没有使用父节点属性，所以需要用变量存储插入位置，以便调整后可以接回到二叉树上。树顶的根节点需特殊处理
static BOOL tree_add(BTree *BT, BTNode *phead, TYPE value)
{//按序插入结点
if(phead == NULL)
return ; if(phead->data == value)
return ; else{
if(phead->data > value){
if(phead->lchild == NULL){
BTNode *newnode = (BTNode*)calloc(, sizeof(BTNode));
newnode->data = value;
newnode->lchild = newnode->rchild = NULL;
phead->lchild = newnode;
}
else{
tree_add(BT, phead->lchild, value); //判断插入节点后是否平衡，并调整
BTNode *root;
if(phead = BT->phead)
root = phead;
else
root = phead->lchild; if(tree_node_height(BT, root->lchild) - tree_node_height(BT, root->rchild) == ){
if(root->lchild->data > value){
root = singleRotateLL(BT, root);
}
else{
root = doubleRotateLR(BT, root);
}
}
phead = root;
}
}
else{
if(phead->rchild == NULL){
BTNode *newnode = (BTNode*)calloc(, sizeof(BTNode));
newnode->data = value;
newnode->lchild = newnode->rchild = NULL;
phead->rchild = newnode;
}
else{
tree_add(BT, phead->rchild, value); //判断插入节点后是否平衡，并调整
BTNode *root;
if(phead = BT->phead)
root = phead;
else
root = phead->rchild; if(tree_node_height(BT, root->rchild) - tree_node_height(BT, root->lchild) == ){
if(root->rchild->data < value){
root = singleRotateRR(BT, root);
}
else{
root = doubleRotateRL(BT, root);
}
}
phead = root;
}
}
phead->height = tree_node_height(BT, phead);
return ;
} return ;
}
第四步，删除
平衡二叉树的删除操作比插入更复杂，因为删除后会引起一系列节点高度的改变，删除后将剩余子树接回二叉树时，要分三种情况处理，被删除节点是：顶部根节点、底部叶子（无子树）、普通节点。
static BOOL tree_del(BTree *BT, BTNode **phead, TYPE value)
{//删除结点
BTNode *temp;
BTNode *root;
int flag; //flag标记被删除的节点，默认顶部节点flag为0，左边节点flag为-1，右边节点flag为1 if(*phead == NULL)
return ; if(*phead == BT->phead){
flag = ;
root = *phead;
} else if((*phead)->lchild != NULL){
flag = -;
root = (*phead)->lchild;
} else if((*phead)->rchild != NULL){
flag = ;
root = (*phead)->rchild;
}
else if((*phead)->lchild == NULL && (*phead)->rchild == NULL)
root = *phead; if(root->data == value){
if(root->lchild != NULL){
temp = BT->search_max(BT, &root->lchild, );
temp->lchild = root->lchild;
temp->rchild = root->rchild;
free(root);
root = temp;
if(flag == )
BT->phead = root;
else
(*phead)->lchild = root;
}
else if(root->rchild != NULL){
temp = BT->search_min(BT, &root->rchild, );
temp->lchild = root->lchild;
temp->rchild = root->rchild;
free(root);
root = temp;
if(flag == )
BT->phead = root;
else
(*phead)->rchild = root;
}
else{
if(flag == )
free(*phead);
else if(flag = -){
free((*phead)->lchild);
(*phead)->lchild = NULL;
}
else if(flag = ){
free((*phead)->rchild);
(*phead)->rchild = NULL;
}
} tree_height(BT, BT->phead); //删除节点后，求每个节点的新高度 if(flag == )
return ;
if(flag == -){
if(tree_node_height(BT, (*phead)->rchild) - tree_node_height(BT, (*phead)->lchild) == ){
if((*phead)->rchild->rchild != NULL){
root = singleRotateRR(BT, *phead);
}
else{
root = doubleRotateRL(BT, *phead);
}
}
}
else{
if(tree_node_height(BT, (*phead)->lchild) - tree_node_height(BT, (*phead)->rchild) == ){
if((*phead)->lchild->lchild != NULL){
root = singleRotateLL(BT, *phead);
}
else{
root = doubleRotateLR(BT, *phead);
}
}
} return ;
}
else if(root->data > value)
return BT->del(BT, &root->lchild, value);
else
return BT->del(BT, &root->rchild, value); return ;
}
除了插入和删除操作，其他操作均与普通二叉查找树一样。
如果读者发现错误或有更好的处理方法，请指出，以便修改完善。
头文件binary.h代码：
#ifndef BINARY_H
#define BINARY_H typedef int TYPE;
typedef int BOOL; typedef struct _BTNode{
TYPE data;
int height;
struct _BTNode *lchild;
struct _BTNode *rchild;
}BTNode; typedef struct _BTree{
BTNode *phead; void(*init)(struct _BTree *BT, TYPE head_value);
void(*exit)(struct _BTree *BT);
void(*print)(struct _BTree *BT, BTNode *phead); BOOL(*add)(struct _BTree *BT, BTNode *phead, TYPE value);
BOOL(*del)(struct _BTree *BT, BTNode **phead, TYPE value);
BOOL(*del_tree)(struct _BTree *BT, BTNode **phead);
BOOL(*alter)(struct _BTree *BT, BTNode *phead, TYPE value, TYPE new_value);
BTNode *(*search)(struct _BTree *BT, BTNode *phead, TYPE value); BTNode *(*search_min)(struct _BTree *BT, BTNode **phead, int flag);
BTNode *(*search_max)(struct _BTree *BT, BTNode **phead, int flag); void(*pre_traverse)(struct _BTree *BT, BTNode *phead);
void(*mid_traverse)(struct _BTree *BT, BTNode *phead);
void(*last_traverse)(struct _BTree *BT, BTNode *phead); //以下为实现AVL所需函数
int (*node_height)(_BTree *BT, BTNode *phead);
void (*height)(_BTree *BT, BTNode *phead);
int (*max_height)(int height1, int height2);
BTNode *(*singleRotateLL)(_BTree *BT, BTNode *phead);
BTNode *(*singleRotateRR)(_BTree *BT, BTNode *phead);
BTNode *(*doubleRotateLR)(_BTree *BT, BTNode *phead);
BTNode *(*doubleRotateRL)(_BTree *BT, BTNode *phead);
}BTree; void tree_init(BTree *BT, TYPE value);
void tree_exit(BTree *BT); #endif
源文件binary.cpp代码：
#include <stdio.h>
#include <string.h>
#include <stdlib.h> #include "binary.h" void tree_init(BTree *BT, TYPE head_value);
void tree_exit(BTree *BT);
void tree_print(BTree *BT, BTNode *phead);
static BOOL tree_add(BTree *BT, BTNode *phead, TYPE value);
static BOOL tree_del(BTree *BT, BTNode **phead, TYPE value);
static BOOL tree_del_tree(BTree *BT, BTNode **phead);
static BOOL tree_alter(BTree *BT, BTNode *phead, TYPE value, TYPE new_value);
static BTNode *tree_search(BTree *BT, BTNode *phead, TYPE value);
static BTNode *tree_search_min(BTree *BT, BTNode **phead, int flag);
static BTNode *tree_search_max(BTree *BT, BTNode **phead, int flag);
static void tree_pre_traverse(BTree *BT, BTNode *phead);
static void tree_mid_traverse(BTree *BT, BTNode *phead);
static void tree_last_traverse(BTree *BT, BTNode *phead); //以下为实现AVL所需函数
static int tree_node_height(BTree *BT, BTNode *phead);
static void tree_height(BTree *BT, BTNode *phead);
static int max_height(int height1, int height2);
static BTNode *singleRotateLL(BTree *BT, BTNode *phead);
static BTNode *singleRotateRR(BTree *BT, BTNode *phead);
static BTNode *doubleRotateLR(BTree *BT, BTNode *phead);
static BTNode *doubleRotateRL(BTree *BT, BTNode *phead); void tree_init(BTree *BT, TYPE head_value)
{//初始化
BT->phead = (BTNode*)calloc(, sizeof(BTNode));
BT->phead->data = head_value; BT->phead->lchild = BT->phead->rchild = NULL; BT->add = tree_add;
BT->del = tree_del;
BT->print = tree_print;
BT->del_tree = tree_del_tree;
BT->alter = tree_alter;
BT->search = tree_search;
BT->search_min = tree_search_min;
BT->search_max = tree_search_max;
BT->pre_traverse = tree_pre_traverse;
BT->mid_traverse = tree_mid_traverse;
BT->last_traverse = tree_last_traverse;
BT->exit = tree_exit; BT->node_height = tree_node_height;
BT->height = tree_height;
BT->max_height = max_height;
BT->singleRotateLL = singleRotateLL;
BT->singleRotateRR = singleRotateRR;
BT->doubleRotateLR = doubleRotateLR;
BT->doubleRotateRL = doubleRotateRL;
} void tree_exit(BTree *BT)
{//结束操作
if(BT != NULL)
BT->del_tree(BT, &BT->phead);
} void tree_print(BTree *BT, BTNode *phead)
{//打印结点
if(phead != NULL)
printf("%d\n", phead->data);
} static BOOL tree_add(BTree *BT, BTNode *phead, TYPE value)
{//按序插入结点
if(phead == NULL)
return ; if(phead->data == value)
return ; else{
if(phead->data > value){
if(phead->lchild == NULL){
BTNode *newnode = (BTNode*)calloc(, sizeof(BTNode));
newnode->data = value;
newnode->lchild = newnode->rchild = NULL;
phead->lchild = newnode;
}
else{
tree_add(BT, phead->lchild, value); //判断插入节点后是否平衡，并调整
BTNode *root;
if(phead = BT->phead)
root = phead;
else
root = phead->lchild; if(tree_node_height(BT, root->lchild) - tree_node_height(BT, root->rchild) == ){
if(root->lchild->data > value){
root = singleRotateLL(BT, root);
}
else{
root = doubleRotateLR(BT, root);
}
}
phead = root;
}
}
else{
if(phead->rchild == NULL){
BTNode *newnode = (BTNode*)calloc(, sizeof(BTNode));
newnode->data = value;
newnode->lchild = newnode->rchild = NULL;
phead->rchild = newnode;
}
else{
tree_add(BT, phead->rchild, value); //判断插入节点后是否平衡，并调整
BTNode *root;
if(phead = BT->phead)
root = phead;
else
root = phead->rchild; if(tree_node_height(BT, root->rchild) - tree_node_height(BT, root->lchild) == ){
if(root->rchild->data < value){
root = singleRotateRR(BT, root);
}
else{
root = doubleRotateRL(BT, root);
}
}
phead = root;
}
}
phead->height = tree_node_height(BT, phead);
return ;
} return ;
} static BOOL tree_del(BTree *BT, BTNode **phead, TYPE value)
{//删除结点
BTNode *temp;
BTNode *root;
int flag; //flag标记被删除的节点，默认顶部节点flag为0，左边节点flag为-1，右边节点flag为1 if(*phead == NULL)
return ; if(*phead == BT->phead){
flag = ;
root = *phead;
} else if((*phead)->lchild != NULL){
flag = -;
root = (*phead)->lchild;
} else if((*phead)->rchild != NULL){
flag = ;
root = (*phead)->rchild;
}
else if((*phead)->lchild == NULL && (*phead)->rchild == NULL)
root = *phead; if(root->data == value){
if(root->lchild != NULL){
temp = BT->search_max(BT, &root->lchild, );
temp->lchild = root->lchild;
temp->rchild = root->rchild;
free(root);
root = temp;
if(flag == )
BT->phead = root;
else
(*phead)->lchild = root;
}
else if(root->rchild != NULL){
temp = BT->search_min(BT, &root->rchild, );
temp->lchild = root->lchild;
temp->rchild = root->rchild;
free(root);
root = temp;
if(flag == )
BT->phead = root;
else
(*phead)->rchild = root;
}
else{
if(flag == )
free(*phead);
else if(flag = -){
free((*phead)->lchild);
(*phead)->lchild = NULL;
}
else if(flag = ){
free((*phead)->rchild);
(*phead)->rchild = NULL;
}
} tree_height(BT, BT->phead); //删除节点后，求每个节点的新高度 if(flag == )
return ;
if(flag == -){
if(tree_node_height(BT, (*phead)->rchild) - tree_node_height(BT, (*phead)->lchild) == ){
if((*phead)->rchild->rchild != NULL){
root = singleRotateRR(BT, *phead);
}
else{
root = doubleRotateRL(BT, *phead);
}
}
}
else{
if(tree_node_height(BT, (*phead)->lchild) - tree_node_height(BT, (*phead)->rchild) == ){
if((*phead)->lchild->lchild != NULL){
root = singleRotateLL(BT, *phead);
}
else{
root = doubleRotateLR(BT, *phead);
}
}
} return ;
}
else if(root->data > value)
return BT->del(BT, &root->lchild, value);
else
return BT->del(BT, &root->rchild, value); return ;
} static BOOL tree_del_tree(BTree *BT, BTNode **phead)
{//删除二叉树
if(*phead == NULL)
return ; if((*phead)->lchild != NULL)
BT->del_tree(BT, &(*phead)->lchild);
if((*phead)->rchild != NULL)
BT->del_tree(BT, &(*phead)->rchild); free(*phead);
*phead = NULL; return ;
} static BOOL tree_alter(BTree *BT, BTNode *phead, TYPE value, TYPE new_value)
{//更改结点的值（先删除，后插入）
if(phead == NULL)
return ; if(value == new_value)
return ; if(BT->del(BT, &phead, value) != ){
if(BT->add(BT, phead, new_value) != )
return ;
else
return ;
}
else
return ;
} static BTNode *tree_search(BTree *BT, BTNode *phead, TYPE value)
{//查找结点
BTNode *temp; if(phead == NULL)
return NULL; if(phead->data == value)
return phead;
if(phead->lchild != NULL){
temp = BT->search(BT, phead->lchild, value);
if(temp != NULL)
return temp;
}
if(phead->rchild != NULL){
temp = BT->search(BT, phead->rchild, value);
if(temp != NULL)
return temp;
} return NULL;
} static BTNode *tree_search_min(BTree *BT, BTNode **phead, int flag)
{//查找最小结点
BTNode *temp; if(*phead == NULL)
return NULL; if((*phead)->lchild == NULL){
temp = *phead;
if(flag == )
*phead = (*phead)->rchild;
return temp;
}
else
return BT->search_min(BT, &(*phead)->lchild, flag);
} static BTNode *tree_search_max(BTree *BT, BTNode **phead, int flag)
{//查找最大结点
BTNode *temp; if(*phead == NULL)
return NULL; if((*phead)->rchild == NULL){
temp = *phead;
if(flag == )
*phead = (*phead)->lchild;
return temp;
}
else
return BT->search_max(BT, &(*phead)->rchild, flag);
} static void tree_pre_traverse(BTree *BT, BTNode *phead)
{//先序遍历二叉树
if(phead == NULL)
return; BT->print(BT, phead);
if(phead->lchild != NULL)
BT->pre_traverse(BT, phead->lchild);
if(phead->rchild != NULL)
BT->pre_traverse(BT, phead->rchild);
} static void tree_mid_traverse(BTree *BT, BTNode *phead)
{//中序遍历二叉树
if(phead == NULL)
return; if(phead->lchild != NULL)
BT->mid_traverse(BT, phead->lchild);
BT->print(BT, phead);
if(phead->rchild != NULL)
BT->mid_traverse(BT, phead->rchild);
} static void tree_last_traverse(BTree *BT, BTNode *phead)
{//后序遍历二叉树
if(phead == NULL)
return; if(phead->lchild != NULL)
BT->last_traverse(BT, phead->lchild);
if(phead->rchild != NULL)
BT->last_traverse(BT, phead->rchild);
BT->print(BT, phead);
} static int tree_node_height(BTree *BT, BTNode *phead)
{//求节点的高度，写成函数解决指针为空的情况，默认空节点的高度为-1，只有一个根节点的节点的高度为0，每多一层高度加1
if(phead != NULL){
if(phead->lchild == NULL && phead->rchild == NULL){
return ;
}
else{
return phead->height = max_height(tree_node_height(BT, phead->lchild), tree_node_height(BT, phead->rchild)) + ;
}
}
else{
return -;
}
} static void tree_height(BTree *BT, BTNode *phead)
{//遍历求树中每个节点的高度
if(phead == NULL)
return; tree_node_height(BT, phead);
if(phead->lchild != NULL)
tree_node_height(BT, phead->lchild);
if(phead->rchild != NULL)
tree_node_height(BT, phead->rchild);
} static int max_height(int height1, int height2)
{//求两个高度的最大值
if(height1 > height2)
return height1;
else
return height2;
} static BTNode *singleRotateLL(BTree *BT, BTNode *phead)
{//不平衡情况为左左的单旋转操作
BTNode *temp; if(phead == NULL)
return ; temp = phead->lchild; if(temp->rchild != NULL){
phead->lchild = temp->rchild;
phead->lchild->height = tree_node_height(BT, phead->lchild);
}
else
phead->lchild = NULL; temp->rchild = phead;
if(temp->rchild->data == BT->phead->data){
BT->phead = temp;
}
phead = temp;
temp->rchild->height = tree_node_height(BT, temp->rchild);
temp->height = tree_node_height(BT, temp);
phead->height = tree_node_height(BT, phead); return phead;
} static BTNode *singleRotateRR(BTree *BT, BTNode *phead)
{//不平衡情况为右右的单旋转操作
BTNode *temp; if(phead == NULL)
return ; temp = phead->rchild; if(temp->lchild != NULL){
phead->rchild = temp->lchild;
phead->rchild->height = tree_node_height(BT, phead->rchild);
}
else
phead->rchild = NULL; temp->lchild = phead;
if(temp->lchild->data == BT->phead->data){
BT->phead = temp;
}
phead = temp;
temp->lchild->height = tree_node_height(BT, temp->lchild);
temp->height = tree_node_height(BT, temp);
phead->height = tree_node_height(BT, phead); return phead;
}
static BTNode *doubleRotateLR(BTree *BT, BTNode *phead)
{//不平衡情况为左右的双旋转操作
BTNode *temp; if(phead == NULL)
return ; temp = phead->lchild;
phead->lchild = singleRotateRR(BT, temp);
temp = phead;
phead = singleRotateLL(BT, temp); return phead;
} static BTNode *doubleRotateRL(BTree *BT, BTNode *phead)
{//不平衡情况为右左的双旋转操作
BTNode *temp; if(phead == NULL)
return ; temp = phead->rchild;
phead->rchild = singleRotateLL(BT, temp);
temp = phead;
phead = singleRotateRR(BT, temp); return phead;
} int main(int argc, char* argv[])
{//测试
BTree testtree;
testtree.init = tree_init;
testtree.init(&testtree, ); testtree.add(&testtree, testtree.phead, );
testtree.add(&testtree, testtree.phead, );
testtree.add(&testtree, testtree.phead, );
testtree.add(&testtree, testtree.phead, );
testtree.add(&testtree, testtree.phead, );
testtree.add(&testtree, testtree.phead, );
testtree.add(&testtree, testtree.phead, );
testtree.add(&testtree, testtree.phead, ); testtree.pre_traverse(&testtree, testtree.phead);
printf("\n");
testtree.mid_traverse(&testtree, testtree.phead);
printf("\n");
testtree.last_traverse(&testtree, testtree.phead);
printf("\n"); printf("%d\n", (testtree.search(&testtree, testtree.phead, ))->data);
printf("\n"); testtree.del(&testtree, &testtree.phead, );
testtree.del(&testtree, &testtree.phead, );
testtree.del(&testtree, &testtree.phead, );
testtree.alter(&testtree, testtree.phead, , ); testtree.pre_traverse(&testtree, testtree.phead);
printf("\n");
testtree.mid_traverse(&testtree, testtree.phead);
printf("\n");
testtree.last_traverse(&testtree, testtree.phead);
printf("\n"); return ;
}
欢迎转载，请备注原始连接http://www.cnblogs.com/liuliuliu/p/3941748.html，并注明转载。
作者bibibi_liuliu，联系方式395985239@qq.com
平衡二叉树（AVL）的实现，附可运行C语言代码的更多相关文章
- 【数据结构】平衡二叉树—AVL树
(百度百科)在计算机科学中,AVL树是最先发明的自平衡二叉查找树.在AVL树中任何节点的两个子树的高度最大差别为一,所以它也被称为高度平衡树.查找.插入和删除在平均和最坏情况下都是O(log n).增 ...
- Java 树结构实际应用 四（平衡二叉树/AVL树）
平衡二叉树(AVL 树) 1 看一个案例(说明二叉排序树可能的问题) 给你一个数列{1,2,3,4,5,6},要求创建一颗二叉排序树(BST), 并分析问题所在. 左边 BST 存在的问题分析: ...
- 数据结构与算法--从平衡二叉树(AVL)到红黑树
数据结构与算法--从平衡二叉树(AVL)到红黑树 上节学习了二叉查找树.算法的性能取决于树的形状,而树的形状取决于插入键的顺序.在最好的情况下,n个结点的树是完全平衡的,如下图"最好情况&q ...
- 二叉查找树（BST)、平衡二叉树(AVL树)（只有插入说明）
二叉查找树(BST).平衡二叉树(AVL树)(只有插入说明) 二叉查找树(BST) 特殊的二叉树,又称为排序二叉树.二叉搜索树.二叉排序树. 二叉查找树实际上是数据域有序的二叉树,即对树上的每个结点, ...
- 二叉查找树（BST)、平衡二叉树(AVL树)
二叉查找树(BST) 特殊的二叉树,又称为排序二叉树.二叉搜索树.二叉排序树. 二叉查找树实际上是数据域有序的二叉树,即对树上的每个结点,都满足其左子树上所有结点的数据域均小于或等于根结点的数据域,右 ...
- 平衡二叉树AVL - 插入节点后旋转方法分析
平衡二叉树 AVL( 发明者为Adel'son-Vel'skii 和 Landis)是一种二叉排序树,其中每一个节点的左子树和右子树的高度差至多等于1. 首先我们知道,当插入一个节点,从此插入点到树根 ...
- 二叉查找树、平衡二叉树(AVL)、B+树、联合索引
1. [定义] 二叉排序树(二拆查找树)中,左子树都比节点小,右子树都比节点大,递归定义. [性能] 二叉排序树的性能取决于二叉树的层数 最好的情况是 O(logn),存在于完全二叉排序树情况下,其访 ...
- 单点登录SSO：可一键运行的完整代码
单点登录方案不同于一个普通站点,它的部署比较繁琐:涉及到好几个站点,要改host.安装证书.配置HTTPS. 看到的不少这方面示例都是基于HTTP的,不认同这种简化: 1. 它体现不出混合HTTP/H ...
- SSL握手通信详解及linux下c/c++ SSL Socket代码举例(另附SSL双向认证客户端代码)
SSL握手通信详解及linux下c/c++ SSL Socket代码举例(另附SSL双向认证客户端代码) 摘自: https://blog.csdn.net/sjin_1314/article/det ...
随机推荐
- Hbase Region Server整体架构
Region Server的整体架构 本文主要介绍Region的整体架构,后续再慢慢介绍region的各部分具体实现和源码 RegionServer逻辑架构图 RegionServer职责 1. ...
- python单元测试框架pytest——fixture函数（类似unitest的setup和teardown）
pytest的setup和teardown函数(曾被一家云计算面试官问到过). pytest提供了fixture函数用以在测试执行前和执行后进行必要的准备和清理工作.与python自带的unitest ...
- JS知识点简单总结
JS(JavaScript) 是一种解释性语言 是弱/动态 最开始用于表单验证的 JS的五个部分: 1.核心语言定义 2.原生对象和内置对象 5boolean 3.BOM 4.DOM 5.事件处理模型 ...
- jvm学习（重点）
http://blog.csdn.net/yfqnihao/article/details/8271665 http://blog.csdn.net/cutesource/article/detail ...
- 此博客可能不再更新，往后博文将发布在 GitHub 中
在 GitHub 上, 可以建立不同的仓库,显示分类可以更明确: 有不同分支,可以打很多次草稿: 用 markdown 语法来书写比较舒服(博客园也可以设置): 最主要的是 GitHub 装逼呀!!! ...
- rowspan && colspan
> 跨行 <html> <body> <table width="> <tr> <th>col1</th> &l ...
- php下获取http状态的实现代码
在项目开发中,有时我们需要知道远程的URL地址是否能访问正常,判断其正常与否后进行下一步的操作,那么在PHP中如何获取远程HTTP的状态呢? 文件preg.php header("HTTP/ ...
- Objective-C 集成农行支付接口
部分参考代码: [NANetworkHandler POSTWithURL:APP_ABCPay par:dict isStored:NO success:^(id responseObject, B ...
- git基础常用维护命令
开发模式介绍 master为生产环境分支 trunk为测试环境分支 开发分支由程序员自己取名 比如来一个新项目之后,下面步骤都是在本地操作 1.从本地获取远程master最新代码,保证本地master ...
- LeetCode——Unique Paths
Question A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram be ...