分类和逻辑回归(Classification and logistic regression)

分类问题和线性回归问题问题很像，只是在分类问题中，我们预测的y值包含在一个小的离散数据集里。首先，认识一下二元分类(binary classification)，在二元分类中，y的取值只能是0和1.例如，我们要做一个垃圾邮件分类器，则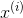为邮件的特征，而对于y，当它1则为垃圾邮件，取0表示邮件为正常邮件。所以0称之为负类（negative class），1为正类（positive class）

逻辑回归

首先看一个肿瘤是否为恶性肿瘤的分类问题，可能我们一开始想到的是用线性回归的方法来求解，如下图：

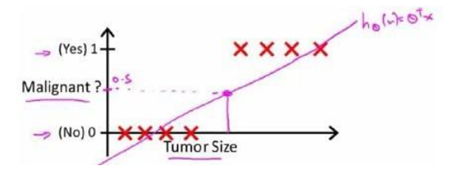
我们知道线性回归问题只能预测连续的值，而分类问题，我们预测值只能够是0或者1，所以我们可能会取一个临界点，大于取1，反之取零。上面的h_Θ(x)好像能够很好的解决问题。所以如下图

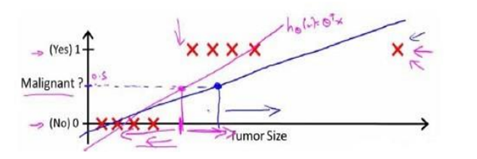
这样还用线性回归模型来求解就显得不合适了，因为它预测的值可以超越[0,1]这个范围。下面我们引入一种新的模型，逻辑回归，它的输出变量范围始终都是在0和1之间。如下：

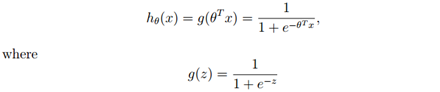
g(z)被称作logistic function或者sigmoid function，它的图像如下：

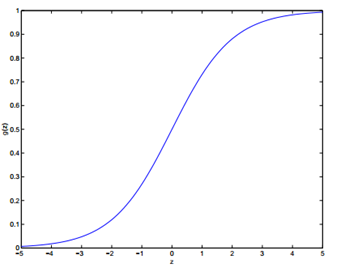
从图像可以看出z → ∞时g(z) →1，z → −∞时g(z) →0。所以令x₀= 1, 则θ^Tx = θ₀+ ∑ⁿ_j=1 θ_jx_j.

在进入正题前，我们先来看logistic function的一个很有用的特征。如下

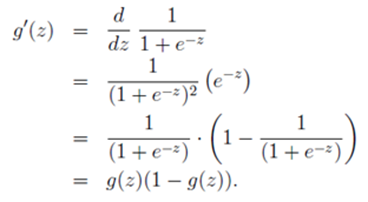
现在回到正题，对于给定的逻辑回归问题，我们怎么去拟合出适合的Θ？

假设：

P (y = 1 | x; θ) = h_θ(x) # hθ(x)的作用是，对于给定的输入变量，根据选择的参数计算输出变量=1 的可能性（ estimated probablity）
P (y = 0 | x; θ) = 1 − h_θ(x)

把上面两个式子整合一下得到：p(y | x; θ) = (h_θ(x))^y (1 − h_θ(x))^1−y

梯度上升方法

在线性回归中，我们的思路是构建似然函数，然后求最大似然估计，最终我们得出了θ的迭代规则，那么在逻辑回归中，我们方法也是一样，因为最后我们是要求最大似然估计，所以用到的算法是梯度上升。

假设训练样本相互独立，则似然函数表达为：

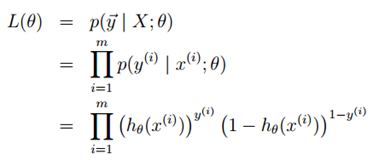
现在我们对似然函数取对数，如下

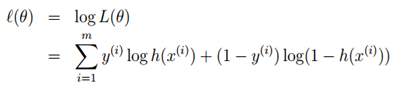
现在我们需要做的就是最大化似然估计了，这里我们就需要用梯度上升方法了。所以用向量来表示的话，更新规则如下

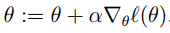
注意：因为我们是最大似然估计，所以这里是正好，而不是负号。

下面我们一一个训练样本为例，使用梯度上升规则:

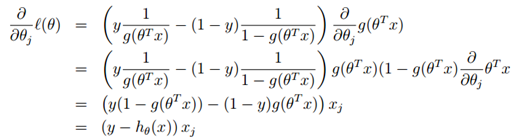
在上面的运算中第二步运用到了我们前面推到的特性g^′(z) = g(z)(1 − g(z))，所以我们得到更新规则：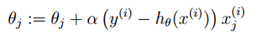

我们发现这个更新规则和LMS算法的更新规则一致，但是应注意这是两个完全不同的算法。在这里 $h_{\theta }(x^{i})$ 是关于 $\theta^{T}x$ 的非线性函数。

这不仅是巧合，更深层次的原因在广义线性模型GLM中会提到。

在前面最大化ℓ(θ)时我们使用到的是梯度上升，在这里，再介绍一种最大化ℓ(θ)的方法---牛顿法（Newton’s method）

牛顿法（Newton’s method）

给出函数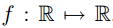：，我们要找到一个Θ使得f(θ) = 0成立，注意这里的Θ∈R，这时牛顿方法的更新规则如下：

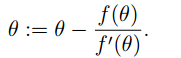
牛顿法的执行过程如下：

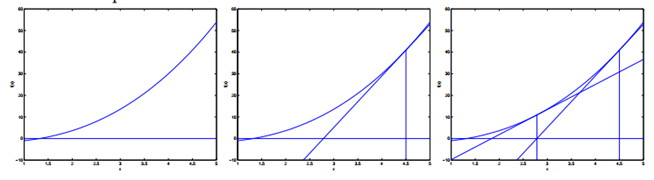
通过求我们给出点的导数对应的切线与x轴的交点为迭代一次后的点，一直反复迭代，直到f(θ) = 0（无限逼近）

所以对于求f(θ) = 0，牛顿法是一种，那么，怎么去用牛顿法来解决最大化ℓ(θ)呢？

沿着思路，当ℓ(θ)最大的时候，ℓ′(θ)=0，所以这样得到更新如下：

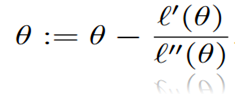
在逻辑回归中，Θ是一个向量，所以此时的牛顿法可以表达为：

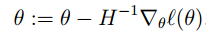
∇θℓ(θ) 表示ℓ(θ)的对θi’s的偏导数，H称为黑塞矩阵(Hessian matrix),是一个n*n的矩阵，n是特征量的个数，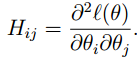

牛顿法的收敛速度比批处理梯度下降要快，它只用迭代很少次就能够很接近最小值，但是n很大的时候，每次迭代求黑塞矩阵和黑塞矩阵的逆代价很大.

最后简单的提一下感知机算法

感知机算法（The perceptron learning algorithm）

将逻辑回归修改一下，现在强制它的输出不是0就是1，则此时的 g就是一个临界函数(threshold function)

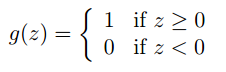
h_θ(x) = g(θ^T x)则我们得到更新规则如下：

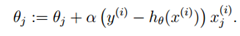
这就是感知机算法。