URAL题解一

URAL题解一

URAL 1002

题目描述：一种记住手机号的方法就是将字母与数字对应，如图。这样就可以只记住一些单词，而不用记住数字。给出一个数字串和n个单词，用最少的单词数来代替数字串，输出对应的任一方案。

solution

首先想到的应该是DP，接着就是状态转移的问题，也就是预处理出每个单词可以与哪一段的数字对应，分析时间复杂度，发现直接暴力判断是可以的，但用HASH会好一些，还可以用KMP。

时间复杂度：\(O(单词数*数字长度)或O(单词长度*数字长度)\)

URAL 1010

题目描述：有一个离散函数，它的定义域为整数\([1, n]\)，现在在函数图象中找两个点，使得这两个点之间的点都在这两个点的连线的下方，求出连线倾斜度最大的方案（两个点，编号小的在前），有多个方案时输出第一个点编号最小的方案。

solution

首先考虑比较特殊的方案：相邻的两个点。相邻的两个点肯定是可行的。然后考虑两点之间有点的可行方案。

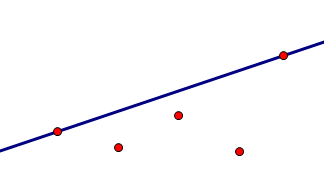
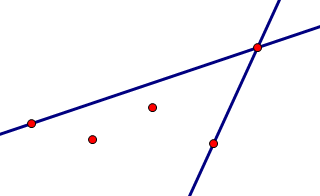
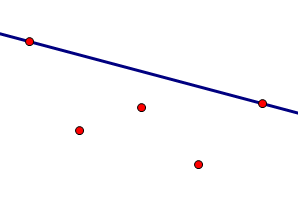
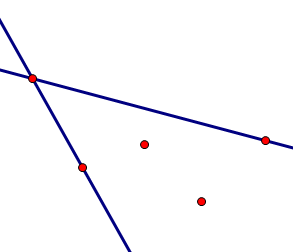
由上图可知，与选取的两点\((i, j)\)相邻的点必定有一个点与i或j相连的直线的倾角比\((i, j)\)所成的直线的倾角要大，所以中间有点的方案不是最优方案，所以答案就是相邻的点形成的直线的倾角最大的方案。

时间复杂度：\(O(n)\)

URAL 1011

题目描述：有\(n\)个人，其中有\(m\)个是乘务员，已知乘务员的比例大于\(P\)%，小于\(Q\)%，问\(n\)最小是多少。

solution

按题意列出公式
$ P$ % \(< \frac{m}{n} < Q\) %
化简
\(P\) % \(n<m< Q\) % \(n\)
题目就变成：找出最小的\(n\)，使得区间\((P\) % \(n ,Q\) % \(n)\)中至少有一个整数。显然\(n<100000\)，所以直接枚举即可。

时间复杂度：\(O(n)\)

URAL 1012

题目描述：在所有没有前导\(0\)的\(n\)位\(k\)进制数中，没有连续两个\(0\)的数有多少个。

solution

很明显是数位DP，但答案很大，要高精度。

时间复杂度：\(O(n^2)\)

URAL 1017

题目描述：用\(n\)个木块排成一个楼梯，楼梯每一级的高度至少要比前一级高一个木块，楼梯至少有两级，问楼梯有多少种。

solution

简单的记忆化搜索，不需要高精度。

时间复杂度：\(O(n^2)\)

URAL 1023

题目描述：有\(n\)颗石子，有两个人进行游戏，轮流拿走石子，每次拿走的石子数目范围为\([1, m]\)，拿走最后一颗的人算赢，请求出最小的\(m(m \geq 2)\)，使得后手必胜。

solution

小学奥数题，显然\(n%(m+1)=0\)时，后手必胜，所以只要求\(n\)的最小因子即可，但要注意\((m \geq 2)\)的限制。

时间复杂度：\(O(\sqrt{n})\)

URAL 1024

题目描述：给出一个关于\(n\)排列的置换\(P\)，问至少需要置换多少次才能变回\(1, 2, 3 ... n\)。(可以证明一定能回到\(1, 2, 3 ... n\))

solution

可以求出每个数至少需要置换多少次才能变回自己，也就是这个数的循环，然后求所有数的循环的最小公倍数就是答案。

时间复杂度：\(O(n^2)\)

URAL 1028

题目描述：给出平面上的\(n\)个点，记每个点的左下方的点的个数为该点的\(level\)，问每个\(level\)有多少个点。

solution

数据已经排好序了，直接用树状数组就好了。

时间复杂度：\(O(nlogn)\)

URAL 1033

题目描述：给出一个展厅的平面图，‘.’是空地，‘#’是墙，展厅外围也是墙，左上角和右下角是入口，所以这两个格子有两面不是墙，现在要给能被游客看到的墙面贴上墙纸，问需要墙纸的面积。

solution

搜索。碰到墙壁就记一次数，或者搜索完后判断某一个面是否是能访问的空地与墙的交界。注意两个入口可能不连通。

时间复杂度：\(O(n^2)\)

URAL 1034

题目描述：一个\(n*n\)的棋盘上有\(n\)个皇后，这\(n\)个皇后两两不能攻击到对方，这时的局面称为peaceful, 问改变任意三个皇后的位置，使得局面依然是peaceful, peaceful的局面有多少个，注意：所有的皇后都看做是相同的。

solution

枚举三个皇后，改变他们的位置（只有两种情况），判断是否peaceful，判断方法与\(n\)皇后问题一样。

时间复杂度：\(O(n^3)\)