2017北京国庆刷题Day3 afternoon

期望得分：100+0+30=130

实际得分：100+36.5+0=136.5

T3 一个变量写混了，丢了30。。

模拟栈

#include<cstdio>
#include<cstring>
using namespace std;
#define N 10001
char s[N];
int st[N],top;
int main()
{
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    scanf("%s",s);
    int len=strlen(s);
    for(int i=;i<len;i++)
        if(s[i]=='(') st[++top]=;
        else if(s[i]=='[') st[++top]=;
        else if(s[i]=='{') st[++top]=;
        else if(s[i]==')')
        {
            if(st[top]==) top--;
            else { printf("Wrong");return ; }
        }
        else if(s[i]==']')
        {
            if(st[top]==) top--;
            else { printf("Wrong"); return ; }
        }
        else
        {
            if(st[top]==) top--;
            else { printf("Wrong"); return ; }
        }
    if(top) printf("Wrong");
    else printf("OK");
    return ;
}

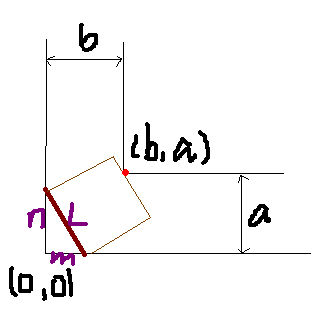
设直线解析式为 y=（-n/m）* x+n

整理，得：n * x + m * y - n * m = 0

点（b，a）到直线的距离为：|  b * n + a * m - n * m | / L

(L : 根号下（n^2 + m^2）=L)

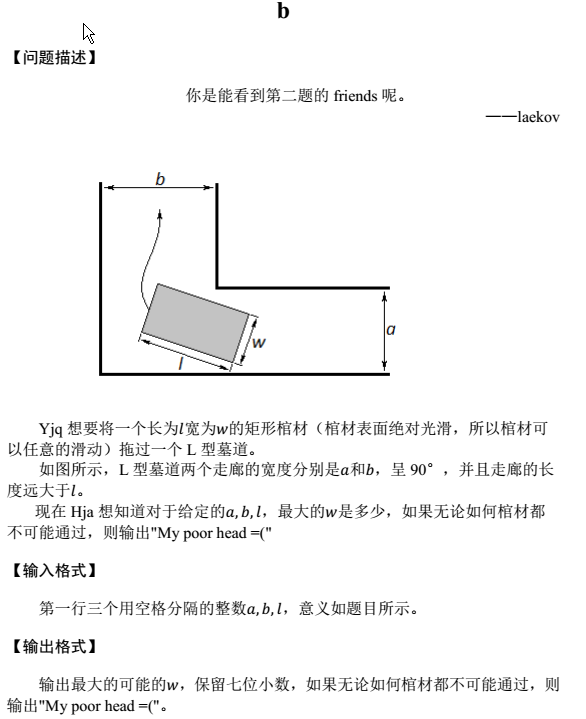
棺材能够在这里拐弯

直观上感受就是棺材拐弯的全程不被点（b，a）卡住

所以 最优解 是  b * n + a * m - n * m / L 的最小值

为什么这里把绝对值去掉？

因为 当式子<0 时，直线到了点的右上方，就是不合法解，此时棺材不能通过

单峰函数求最小值，三分法每次去掉大的一部分

注意特判直接横着/竖着就能拖过去的情况

#include<algorithm>
#include<cstdio>
#include<cmath>

using namespace std;
const double eps=1e-;

int a,b,l;

double f(double n)
{
    double m=sqrt(1.0*l*l-n*n);
    return (b*n+a*m-n*m)/l;
}

int main()
{
    freopen("b.in","r",stdin);
    freopen("b.out","w",stdout);
    scanf("%d%d%d",&a,&b,&l);
    if(a>=l && b>=l) { printf("%d.0000000",l); return ; }
    if(a>=l) { printf("%d.0000000",b); return ; }
    if(b>=l) { printf("%d.0000000",a); return ; }
    double L=,R=l,ans=-1e18,mid1,mid2,t1,t2;
    int T=;
    while(T--)
    {
        mid1=(R-L)/+L; mid2=L+R-mid1;
        t1=f(mid1); t2=f(mid2);
        if(t1< || t2<) { printf("My poor head =("); return ; }
        if(t1<t2) ans=t1,R=mid2;
        else ans=t2,L=mid1;
    }
    printf("%.7lf",ans);
}

递归回溯时贪心

如果当前点的分支个数>=2，那么断掉它与父节点的边，子节点中只留两个最优

所以 ans+=分支个数-2+1

加1是因为还要断掉与父节点的连边

但是如果是递归的根节点，就是ans+=分支个数-2

如果当前只有一个分支，那就不用断，仍然是它的父节点的一个分支

最终的答案就是ans*2+1

*2是因为断掉一个，相应的就要添加一条

+1是最后要形成一个环

#include<cstdio>
#include<iostream>

#define N 100001

using namespace std;

int front[N],nxt[N<<],to[N<<],tot;
int ans;

void read(int &x)
{
    x=; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*+c-''; c=getchar(); }
}

void add(int u,int v)
{
    to[++tot]=v; nxt[tot]=front[u]; front[u]=tot;
    to[++tot]=u; nxt[tot]=front[v]; front[v]=tot;
}

int dfs(int x,int f)
{
    int sum=;
    for(int i=front[x];i;i=nxt[i])
        if(to[i]!=f) sum+=dfs(to[i],x);
    if(sum>=)
    {
        if(x==) ans+=sum-;
        else ans+=sum-;
        return ;
    }
    return ;
}

int main()
{
    freopen("c.in","r",stdin);
    freopen("c.out","w",stdout);
    int n,u,v;
    read(n);
    for(int i=;i<n;i++) read(u),read(v),add(u,v);
    dfs(,);
    printf("%d",ans*+);
}