NOIP模拟赛12

期望得分：100+100+50=250

实际得分：100+100+30=230

A 约数之和(count.pas/c/cpp)

TL:1S ML:128MB
【Description】
我们用 D(x)表示正整数 x 的约数的个数。给定一个正整数 N，求 D(1)+D(2)+…+D(N)。
【Input】
一行一个正整数 N。
【Output】
一行一个整数，表示答案
【Sample Input】
5
【Sample Output】
10
【Hint】
样例解释：
D(1)=1 D(2)=2
D(3)=2 D(4)=3 D(5)=2
对于 20%的测试数据：N<=1000
对于 50%的测试数据：N<=100000
对于 100%的测试数据：N<=10000000

枚举i，那么i是n/i个数的约数

#include<cstdio>
using namespace std;
int main()
{
    freopen("count.in","r",stdin);
    freopen("count.out","w",stdout);
    int n,ans=;
    scanf("%d",&n);
    for(int i=;i<=n;i++) ans+=n/i;
    printf("%d",ans);
}

B 邮局选址(post.pas/c/cpp)

TL:1S ML:128MB
【Description】
在 J 市的一条笔直的公路旁分布着 n 个村庄，每个村庄都有一个唯一的坐标 Xi，任意一
对村庄的坐标不同。最近，J 市领导计划在村庄里新建 m 个邮局，而邮局在 n 个村庄里
的分布情况会影响到居民的便利程度。
设 m 个邮局分别建在 P1,P2,..,Pm 号村庄。每个村庄的村民都会找到与其距离最近的一
个邮局， 若有多个距离最近的则会任选一个， 该村庄的便利度即为该村庄与其最近的邮局的
距离，而所有村庄的便利度的和即为总便利度。
严格地讲，总便利度 C 定义为
∑min⁡ {|?? − ???|⁡(1 ≤ ? ≤ ?)}
?
?=1
现在，由你来安排邮局的建设位置。请计算最小的 C 是多少。
【Input】
第一行两个整数 n m
第二行递增的 n 个整数，表示 X1..Xn
【Output】
一行一个整数，表示最小的 C
【Sample Input】
10 5
1 2 3 6 7 9 11 22 44 50
【Sample Output】
9
【Hint】
样例解释：建立在坐标为：2 7 22 44 50 的位置
每个村庄的便利度分别为：1 0 1 1 0 2 4 0 0 0
对于 30%的测试数据 n ≤ 10
对于 60%的测试数据 n ≤ 50
对于 100%的测试数据 1 ≤ n ≤ 300; 1 ≤ m ≤ 30; m ≤ n; 1 ≤ Xi ≤ 10000

考场思路：

dp[i][j] 表示前i个村庄，放了j个邮局，一定有一个邮局在第i个村庄最小的C

预处理dis[i][j]表示两个相邻的邮局一个在i，一个在j，村庄i到村庄j的最小的C

dp[i][j]=min(dp[k][j-1]+dis[k][i])

最后再把第n个村庄不放邮局合并进去

#include<cstdio>
#include<cstring>
#define N 301
#define M 31
using namespace std;
int pos[N];
int dis[N][N],dp[N][M],last[N];
int abs(int i) { return i< ? -i : i; }
int min(int i,int j) { return i<j ? i : j; }
int main()
{
    freopen("post.in","r",stdin);
    freopen("post.out","w",stdout);
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++) scanf("%d",&pos[i]);
    int mid;
    for(int i=;i<n;i++)
        for(int j=i;j<=n;j++)
            for(int k=i;k<=j;k++)
                if(pos[k]-pos[i]<pos[j]-pos[k]) dis[i][j]+=pos[k]-pos[i];
                else dis[i][j]+=pos[j]-pos[k];
    memset(dp,,sizeof(dp));
    for(int i=;i<=n;i++)
    {
        dp[i][]=;
        for(int k=;k<=i;k++) dp[i][]+=abs(pos[k]-pos[i]);
    }
    for(int i=;i<n;i++)
        for(int j=i+;j<=n;j++)
            last[i]+=abs(pos[j]-pos[i]);
    for(int i=;i<=n;i++)
        for(int j=;j<=min(i,m);j++)
            for(int k=;k<i;k++)
                dp[i][j]=min(dp[i][j],dp[k][j-]+dis[k][i]);
    for(int i=;i<=n;i++) dp[n][m]=min(dp[n][m],dp[i][m]+last[i]);
    printf("%d",dp[n][m]);
}

std思路：

dp[i][j]前i个村庄，放了j个邮局

预处理cost[i][j] 表示村庄i到村庄j 共用一个邮局，那么这个邮局肯定放在中位数位置

dp[i][j]=min(dp[k][j-1]+cost[k+1][i])

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m, p[], f[][], cost[][];
int main()
{
    freopen("post.in", "r", stdin); freopen("post.out", "w", stdout);
    scanf("%d%d", &n, &m);
    for (int i = ; i <= n; i++) scanf("%d", &p[i]);
    for (int i = ; i <= n; i++)
        for (int j = i; j <= n; j++){
            cost[i][j] = ;
            int k = (i + j) >> ;
            for (int t = i; t <= j; t++)
                cost[i][j] += abs(p[k] - p[t]);
            }
    memset(f, 0x3f, sizeof(f)); f[][] = ;
    for (int i = ; i <= n; i++)
        for (int j = ; j <= m; j++)
            for (int k = ; k <= i - ; k++)
                f[i][j] = min(f[i][j], f[k][j - ] + cost[k + ][i]);
    printf("%d\n", f[n][m]);
}

C 分数(fraction.pas/c/cpp)

TL:2S ML:128MB
【Description】
在一门叫做计算机应用数学的神奇的课上，老师教给大家如何处理小数的进制转换：
p 进制的小数 abc.def 的十进制值为：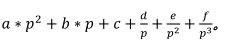 

例如十进制数 1
3 在十进制下小数表示为 0.33333…， 在三进制下为 0.1， 在三十进制下为 0.A。
（这里 A 的含义与十六进制中 A 的含义相同，均表示 10） 。
下课后，老师要求 kAc 将 N 个十进制的分数写成 k 进制下的小数。然而 kAc 发现，很多十
进制分数根本不可能写成有限的 k 进制小数！这令他十分不爽，不过他想知道，最小需要几
进制才能使得这些十进制分数在该进制下均为有限的小数。
【Input】
第一行两个整数 N
接下来 N 行，每行两个整数 a, b，表示一个十进制小数 a
b 。
【Output】
一个整数，表示最小进制数。这里，请按照十六进制输出，所有字母全部大写。 （例如，如
果答案为十进制下 26，则输出 1A） 。
【Sample Input】
2
3 99
1 99
1 11
【Sample Output】
21
【Hint】
样例解释：
在 33 进制下，
3
99 可以表示为 0.1，
1
99 可以表示为 0.0B，
1
11 可以表示为 0.3。
可以证明不存在更小的进制，使得他们均为有限小数。
对于 20%的测试数据：n=1
对于 50%的测试数据： n<=10， a, b <= 10000， 保证最终答案在十进制下不超过 10000。
对于 70%的测试数据：n<=100，a, b<= 10000。
对于 100%的测试数据：n<=1000，1 <= a,b <= 1000000000。

首先把分数约成最简

然后结果只跟分母有关

打表可以发现，如果a/b可以表示成n进制，那么有

对b分解质因数:b=p1^k1 * p2^k2 * ……

n = m* p1*p2*p3 ，m∈Z+

所以对所有的分母分解质因数，取最小公倍数即为答案

求最小公倍数时，涉及高精，不要用a*b/gcd（a，b）

将所有分解质因数的p乘起来即可

map判断这个p有没有被乘进去过

#include<cstdio>
#include<cstring>
#include<map>
using namespace std;
const int MO=;
struct Big
{
        int len,data[];
        void clear() { memset(this,,sizeof(*this));}
        int & operator [] (int k) { return data[k] ; }
        Big operator = (int k)
        {
                clear();
                len=;
                while(k)
                {
                        ++len; data[len]=k&MO; k>>=;
                }
                if(!len) ++len;
                return *this;
        }
        Big operator * (Big A)
        {
                Big tmp; tmp.clear(); tmp.len=len+A.len-;
                for(int i=;i<=len;i++)
                        for(int j=;j<=A.len;j++)
                        {
                                tmp[i+j-]+=A[j]*data[i];
                                tmp[i+j]+=(tmp[i+j-]>>);
                                tmp[i+j-]&=MO;
                        }
                while(tmp[tmp.len+]) ++tmp.len;
                return tmp;
        }
        void print()
        {
                for(int i=len;i;i--) printf("%X",data[i]);
        }
}tmp,ans;
map<int,bool>M;
int pnum,p[];
bool f[];
void GETP(int M)
{
        memset(f,,sizeof(f));
        for(int i=;i<=M;i++)
        {
                if(!f[i]) p[++pnum]=i;
                for(int j=;j<=pnum;j++)
                {
                        if(i*p[j]>M) break;
                        f[i*p[j]]=true;
                        if(i%p[j]==) break;
                }
        }
}
int gcd(int  a,int b) { return !b ? a : gcd(b,a%b);}
void work(int num)
{
        for(int i=;i<=pnum;i++)
                if(num%p[i]==)
                {
                        if(M[p[i]]==)
                        {
                                M[p[i]]=true;
                                tmp=p[i];
                                ans=ans*tmp;
                        }
                        while(num%p[i]==) num/=p[i];
                }
        if(num!=)
                if(M[num]==)
                {
                        M[num]=true;
                        tmp=num;
                        ans=ans*tmp;
                }
}
int main()
{
        ans=;
        int t,a,b;
        scanf("%d",&t);
        GETP();
        while(t--)
        {
                scanf("%d%d",&a,&b);
                int d=gcd(a,b); a/=d,b/=d;
                work(b);
        }
        ans.print();
}