HDU - 2973：YAPTCHA （威尔逊定理）

The math department has been having problems lately. Due to immense amount of unsolicited automated programs which were crawling across their pages, they decided to put Yet-Another-Public-Turing-Test-to-Tell-Computers-and-Humans-Apart on their webpages. In short, to get access to their scientific papers, one have to prove yourself eligible and worthy, i.e. solve a mathematic riddle.

However, the test turned out difficult for some math PhD students and even for some professors. Therefore, the math department wants to write a helper program which solves this task (it is not irrational, as they are going to make money on selling the program).

The task that is presented to anyone visiting the start page of the math department is as follows: given a natural n, compute
   

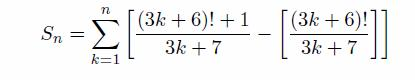
where [x] denotes the largest integer not greater than x.

InputThe first line contains the number of queries t (t <= 10^6). Each query consist of one natural number n (1 <= n <= 10^6).OutputFor each n given in the input output the value of Sn.Sample Input

13
1
2
3
4
5
6
7
8
9
10
100
1000
10000

Sample Output

0
1
1
2
2
2
2
3
3
4
28
207
1609

 题意：求这个公式的前缀和。

思路：不难发现，式子里做减法要么为1.要么为0，为1当且仅当((3k+6)!+1)%(3k+7)==0；

然后我就不知道了，百度了下原来就是威尔逊定理：p是素数的充分必要条件是，((p-1)!+1)%p==0；

#include<bits/stdc++.h>
using namespace std;
const int maxn=;
int p[maxn],vis[maxn],ans[maxn],cnt;
void solve()
{
    vis[]=;
    for(int i=;i<maxn;i++){
        if(!vis[i]) p[++cnt]=i;
        for(int j=;j<=cnt&&p[j]*i<maxn;j++){
            vis[i*p[j]]=;
            if(!(i%p[j])) break;
        }
    }
}
int main() {
    solve();
    int T,N; scanf("%d",&T);
    for(int i=;i<=;i++) ans[i]=ans[i-]+(!vis[*i+]);
    while(T--){
        scanf("%d",&N);
        printf("%d\n",ans[N]);
    }
    return ;
}