[转]Kerberos简介

Kerberos协议：

Kerberos协议主要用于计算机网络的身份鉴别(Authentication), 其特点是用户只需输入一次身份验证信息就可以凭借此验证获得的票据(ticket-granting ticket)访问多个服务，即SSO(Single Sign On)。由于在每个Client和Service之间建立了共享密钥，使得该协议具有相当的安全性。

条件

先来看看Kerberos协议的前提条件：

如下图所示，Client与KDC， KDC与Service 在协议工作前已经有了各自的共享密钥，并且由于协议中的消息无法穿透防火墙，这些条件就限制了Kerberos协议往往用于一个组织的内部， 使其应用场景不同于X.509 PKI。

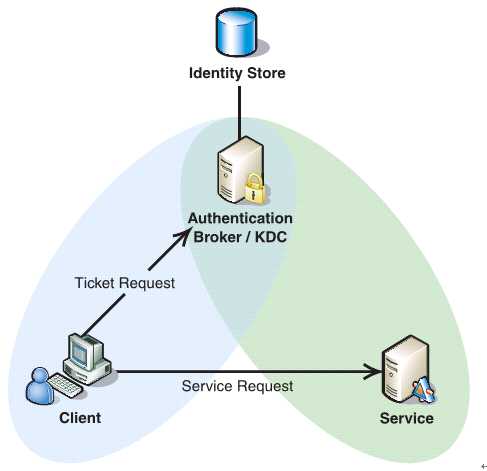
过程

Kerberos协议分为两个部分：

1 . Client向KDC发送自己的身份信息，KDC从Ticket Granting Service得到TGT(ticket-granting ticket)， 并用协议开始前Client与KDC之间的密钥将TGT加密回复给Client。

此时只有真正的Client才能利用它与KDC之间的密钥将加密后的TGT解密，从而获得TGT。

（此过程避免了Client直接向KDC发送密码，以求通过验证的不安全方式）

2. Client利用之前获得的TGT向KDC请求其他Service的Ticket，从而通过其他Service的身份鉴别。

Kerberos协议的重点在于第二部分，简介如下：

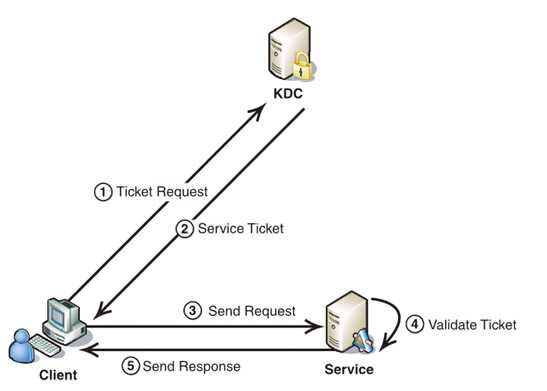
1．    Client将之前获得TGT和要请求的服务信息(服务名等)发送给KDC，KDC中的Ticket Granting Service将为Client和Service之间生成一个Session Key用于Service对Client的身份鉴别。然后KDC将这个Session Key和用户名，用户地址（IP），服务名，有效期, 时间戳一起包装成一个Ticket(这些信息最终用于Service对Client的身份鉴别)发送给Service， 不过Kerberos协议并没有直接将Ticket发送给Service，而是通过Client转发给Service.所以有了第二步。

2．    此时KDC将刚才的Ticket转发给Client。由于这个Ticket是要给Service的，不能让Client看到，所以KDC用协议开始前KDC与Service之间的密钥将Ticket加密后再发送给Client。同时为了让Client和Service之间共享那个秘密(KDC在第一步为它们创建的Session Key)， KDC用Client与它之间的密钥将Session Key加密随加密的Ticket一起返回给Client。

3．    为了完成Ticket的传递，Client将刚才收到的Ticket转发到Service. 由于Client不知道KDC与Service之间的密钥，所以它无法算改Ticket中的信息。同时Client将收到的Session Key解密出来，然后将自己的用户名，用户地址（IP）打包成Authenticator用Session Key加密也发送给Service。

4．    Service 收到Ticket后利用它与KDC之间的密钥将Ticket中的信息解密出来，从而获得Session Key和用户名，用户地址（IP），服务名，有效期。然后再用Session Key将Authenticator解密从而获得用户名，用户地址（IP）将其与之前Ticket中解密出来的用户名，用户地址（IP）做比较从而验证Client的身份。

5．    如果Service有返回结果，将其返回给Client。

总结

概括起来说Kerberos协议主要做了两件事

1．    Ticket的安全传递。

2．    Session Key的安全发布。

再加上时间戳的使用就很大程度上的保证了用户鉴别的安全性。并且利用Session Key，在通过鉴别之后Client和Service之间传递的消息也可以获得Confidentiality(机密性), Integrity(完整性)的保证。不过由于没有使用非对称密钥自然也就无法具有抗否认性，这也限制了它的应用。不过相对而言它比X.509 PKI的身份鉴别方式实施起来要简单多了。

推荐资料：

Kerberos的原理

Kerberos: An Authentication Service for Computer Networks

Web Services Security系列文章