四元数运动学笔记(5)IMU驱动的运动误差方程
1.1线性化卡尔曼滤波
1.2偏差微分方程的推导
1.3线性化卡尔曼滤波的流程
1.4 离散EKF
2.误差状态的运动方程
2.1连续时间的IMU系统动态方程
2.1.1相关变量
2.1.2真实状态运动方程(true-state kinematics equations )
2.1.3标称状态运动方程(normal-state kinematics equations )
2.1.4误差状态运动方程
2.2离散时间的IMU系统动态方程
2.2.1离散时间的IMU系统动态方程
2.2.2误差状态的雅克比矩阵和扰动矩阵
3.ESKF:Error state Kalman filter
3.1总体介绍
3.2ESKF vs KF
3.3fusing IMU with other complementary sensory data
3.3.1ESKF prediction
3.3.2ESKF correction
3.2.1 通过correction建立误差的观测
3.2.2 将观测误差注入标称状态
3.2.3ESKF reset
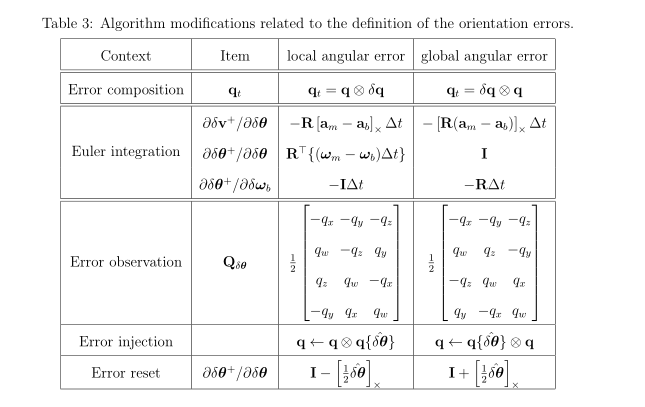
3.4 使用global angular errors的ESKF
3.4.1 连续时间误差状态运动方程
3.4.2 离散误差状态运动方程
3.4.3 globally ESKF vs locally ESKF
1.扩展卡尔曼滤波EKF
1.1线性化卡尔曼滤波
- 标称值(normal value):标称值是基于系统轨迹的先验猜测,比如系统方程代表飞行的动态性能,则标称控制、状态和输出可能的飞行轨迹。标称值是没有任何噪声和模型扰动的理想值,它和世界的轨迹(true-sate真实值)之间的各种因素产生的不确定性用误差δx" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">δx表示。
- 系统的运动学方程一般采用状态变量的微分形式表示,从而建立微分方程,将问题代数化。我的理解是,右边的函数以系统相关参数表示出了左边状态变量的变化速率。
- 非线性系统方程的泰勒级数展开
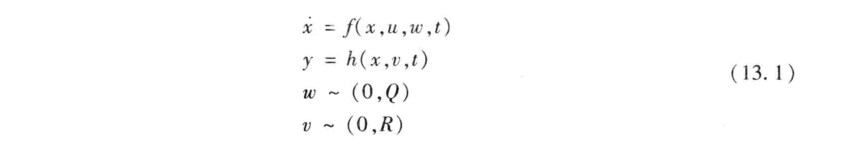
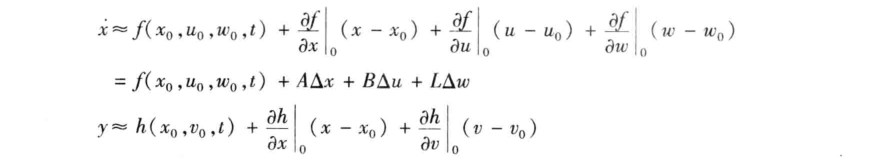
1.2偏差微分方程的推导
- 需要注意的是这里假设真实的控制输入是没有不确定性的,即使有也将其归于过程噪声里。

1.3线性化卡尔曼滤波的流程

1.4 离散EKF

2.误差状态的运动方程
- 这里涉及到真实值(true-),标称值(nominal-),和误差状态值(error-state)三个量,真实值是有标称值和误差值组合而来。标称值是有非线性方程而来的"大信号",误差值的线性方程而来满足线性高斯滤波的“小信号”。
2.1连续时间的IMU系统动态方程
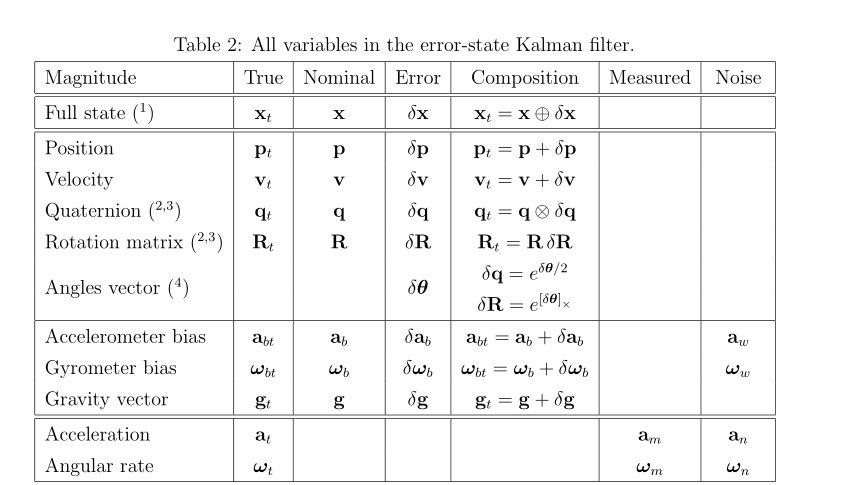
2.1.1相关变量
- 这里的相关变量中,输入值是IMU的测量值am,bm" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">am,bm,以及当地重力加速度g" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">g;其他真值值变量的值都是由他们而来。其中normal值是一个抽象变量,表示理想值,是无法估计的。在融合中我们使用估计的真实值做为预测。
- 标称值是完全理想值,我们把各种因素产生的真实值和标称值的不确定性归于变量δx" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">δx表示。
- 这里采用Hamilton 四元数的表述方法
- 这里的角速率w" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">w使用的是locally的表述,这样可以直接使用机体系b下的传感器测量值wm" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">wm。
- 这里的角度误差δθ" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">δθ使用的也是locally的表述,这是很多文献和算法采用的经典方式,不过有证明说采用globally的方式定义的角度误差有更好的性质。
- 这里的加速度a" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">a定义的是globally,我的理解是,方便计算导航系下的速度和位置。
2.1.2真实状态运动方程(true-state kinematics equations )
- true-state 变量表示的运动方程.IMU bias的噪声定义为随机游走。
由于初始状态姿态未知,这种不确定即重力加速度向量的不确定,但是实际工程中我们是制定初始状态的,即重力加速度不确定不再存在,这里的方程也认为其为恒定值。
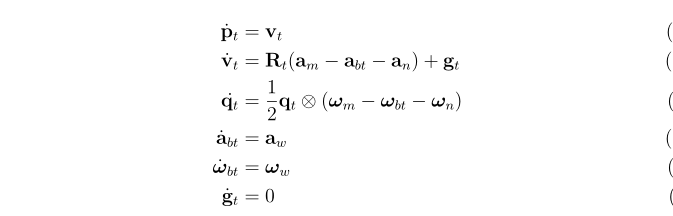
IMU误差来源分为两种,内部biasabt,wbt" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">abt,wbt和测量噪声an,wn" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">an,wn.
这里的IMU真实值是没有bias和测量噪声的值,IMU加速度计测量加速度不包含重力加速度,即如果自由落体运动,不考虑噪声加速度计的读数是0。
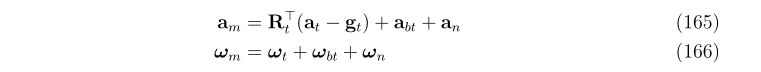
利用IMU测量代替真实值的系统真实状态运动方程x˙=ft(xt,u,w)" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">x˙=ft(xt,u,w),该方程状态为xt" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">xt,由IMU的含噪声测量值um" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">um驱动,并受高斯白噪声w" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">w干扰.
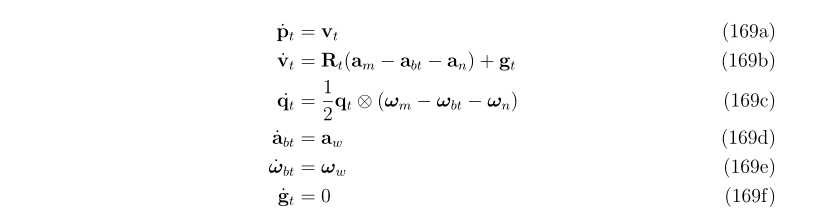
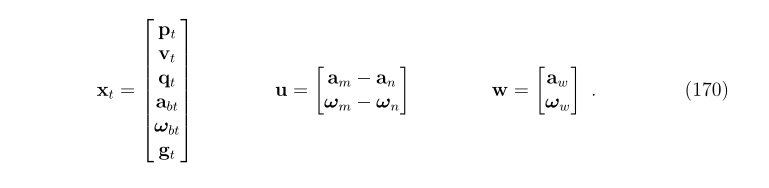
2.1.3标称状态运动方程(normal-state kinematics equations )
- 标称状态对应系统没有噪声和扰动的情况。
- 可以这么理解,标称值是把测量值am,wm" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">am,wm和bias当做理想值计算出来的理想状态;而实际值是在考虑测量值和bias有一部分应该不是我们想要的信号,是测量值减去噪声和bias减去扰动计算得到的。我们的目的是优化两者的误差,误差越小,测量值和bias包含的不确定性就越小。
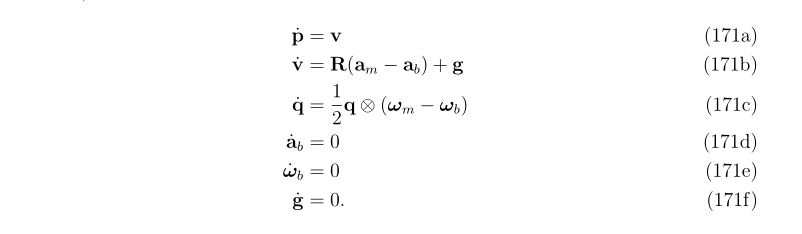
2.1.4误差状态运动方程
方程的右边变量是标称状态、IMU测量值和噪声项。
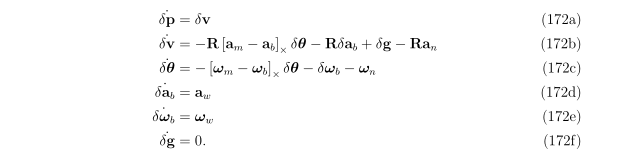
其中速度误差和角度误差推导如下,主要技巧是省略小量的二次以上的项以及真实值和标称值之间的数学关系。还有就是高斯噪声的各向同性,使旋转对其没有影响。


2.2离散时间的IMU系统动态方程
2.2.1离散时间的IMU系统动态方程
误差状态运动方程的离散化主要是利用其微分方程进行积分,并将其表示为迭代形式。积分的方法有很多种。
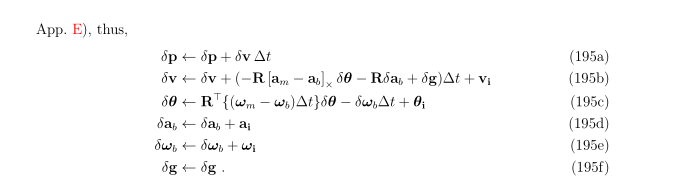
离散化后的噪声和连续状态的噪声存在差别,详细见IMU Noise Model.

2.2.2误差状态的雅克比矩阵和扰动矩阵
- 通过观察2.2.1很容易得到误差状态迭代方程的的雅克比矩阵;这里给出的是离散迭代方程的雅克比,和连续情况下误差状态的微分方程的雅克比,会有些不同。
- 这里的雅克比矩阵其实就是误差状态方程的状态转移矩阵。
- 这里的雅克比矩阵来源于真实状态运动方程的离散化,即2.2.4误差状态运动方程的推导过程即是其离散化的过程。


3.ESKF:Error state Kalman filter
3.1总体介绍
- 这里介绍sola的ESKF,其中的误差来源是IMU加速度计和陀螺仪读数噪声以及bias带的扰动。首先推导了IMU的系统误差动态方程,由于IMU造成的航位推算系统(DR:dead-reckoning position system)会随着时间漂移(我的理解是由于在只有IMU作为测量传感器的位姿测量系统里,航向角和位置都是靠积分得到的,因而会有航位的漂移问题)。所以将该方程做为KF的预测值,使用其他来源的数据如GPS或视觉作为矫正,构成融合数据的KF。
- 我的理解,作者这里提出的ESKF,和EKF其实是一回事。
3.2ESKF vs KF
- 作者比较了ESKF相对于KF的优点,有些不是完全理解
- 避免参数冗余,由于ESKF的参数和自由度一致,可以避免协方差矩阵的奇异性问题。
- ESKF的(误差)变量操作一直在原点附近(误差变量的值很小),可以避免可能地参数奇异性、万向节锁的问题,保证线性化的有效性。
- 误差状态值一致很小,意味着公式中误差的二次以乘积都可以忽略,使得相应的雅克比矩阵比较简单,提高计算速度。
- 可以让KF的correction速度低于prediction,这点不是很理解,贴在这里吧。

3.3fusing IMU with other complementary sensory data
3.3.1ESKF prediction
- 具体变量定义见2.3.2,在2.2.3中,我们使用IMU含噪声的测量值和bias去计算标称值。并且没有考虑测量值的噪声项和扰动,从而产生了误差。我们把所有不确定性引来的误差放在误差变量δx" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">δx中考虑,我们利用IMU测量值和高斯噪声去计算误差项,并将其作为ESKF的观测,并利用其它来源的数据如GPS,视觉等来作为矫正(使误差可观)。
- 这里用IMU作为观测,不是完全理解,我现在的理解是,IMU数据的引入使得预测项更加接近真实情况,参考《最优状态估计》,这里的IMU数据即运动方程里的控制项,如果没有测量值做控制项,我们需要进行比较强的假设,如恒速模型等;但是有了传感器数据作为控制输入,运动方程的模型就更加接近真实情况,有时我们也用里程计作为控制输入,但相对于IMU,里程计的测量位置误差会比较大(齿轮啮合不理想等),而且对于飞行器来说,里程计是不能用的。
- 最后我们利用上次的状态值、控制输入、传递的误差项来预测下一时刻的状态。
- 预测阶段均值和方差的更新公式:

3.3.2ESKF correction
3.2.1 通过correction建立误差的观测
这里使用另外的GPS或camera建立测量方程,并将观测方程在标称点附近进行线性化。

这里的雅克比矩阵推导使用了链式法则。


3.2.2 将观测误差注入标称状态
- 这样做使得这次迭代标称状态和真实状态相等,误差重置为0;

3.2.3ESKF reset
重置的过程主要涉及到不确定性即方差的传播,通常这里的雅克比可以近似为I。

这里的雅克比矩阵的推导

3.4 使用global angular errors的ESKF
- 之前有提到使用global angular error有更好的特性,这里进行相关的推导,所以涉及到的旋转积分要采用globally的左扰动。
- 这里的角速度仍使用locally,考虑到测量值是在机体系下表示的
3.4.1 连续时间误差状态运动方程

- 相关推导和locally相似,在角度误差微分方程推导里,四元数微分用的是locally,四元数积分用的是globally,这样做的可行性在于角度误差和角速率没有耦合在两者中使用。


3.4.2 离散误差状态运动方程

3.4.3 globally ESKF vs locally ESKF
四元数运动学笔记(5)IMU驱动的运动误差方程的更多相关文章
- 从零开始一起学习SLAM | 用四元数插值来对齐IMU和图像帧
视觉 Vs. IMU 小白:师兄,好久没见到你了啊,我最近在看IMU(Inertial Measurement Unit,惯性导航单元)相关的东西,正好有问题求助啊 师兄:又遇到啥问题啦? 小白:是这 ...
- input子系统学习笔记六 按键驱动实例分析下【转】
转自:http://blog.chinaunix.net/uid-20776117-id-3212095.html 本文接着input子系统学习笔记五 按键驱动实例分析上接续分析这个按键驱动实例! i ...
- AM335x(TQ335x)学习笔记——GPIO关键驱动移植
或按照S5PV210学习秩序.我们首先解决的关键问题.TQ335x有六个用户按钮,每个上.下.剩下.对.Enter和ESC. 我想开始学习S5PV210当同一,写输入子系统驱动器的关键问题要解决,但浏 ...
- AM335x(TQ335x)学习笔记——GPIO按键驱动移植
还是按照S5PV210的学习顺序来,我们首先解决按键问题.TQ335x有六个用户按键,分别是上.下.左.右.Enter和ESC.开始我想到的是跟学习S5PV210时一样,编写输入子系统驱动解决按键问题 ...
- MongoDB学习笔记~关于官方驱动集成IQueryable之后的一些事
回到目录 关于官方驱动集成IQueryable之后的一些事,有好事也有坏事,好事就是它会将你的linq语句非常友好的翻译成MongoDB语句,而坏事就是有一些linq语句不会被翻译,不会被翻译的代价就 ...
- Linux 驱动学习笔记05--字符驱动实例,实现一个共享内存设备的驱动
断断续续学驱动,好不容易有空,做了段字符驱动的例子.主要还是跟书上学习在此记录下来,以后说不定能回过头来温故知新. 首先上驱动源码 gmem.c: /************************* ...
- linux 驱动学习笔记04--简单驱动
首先贴代码helloworld.c和Makefile /************************************************************************ ...
- Yocto开发笔记之《驱动调试-华为3G模块》(QQ交流群:519230208)
QQ群:519230208,为避免广告骚扰,申请时请注明 “开发者” 字样 ======================================================== 参考:ht ...
- AM335x(TQ335x)学习笔记——Nand&&网卡驱动移植
移植完成声卡驱动之后本想再接再励,移植网卡驱动,但没想到的是TI维护的内核太健壮,移植网卡驱动跟之前移植按键驱动一样简单,Nand驱动也是如此,于是,本人将Nand和网卡放在同一篇文章中介绍.介绍之前 ...
随机推荐
- 【379】pandas 说明
参考:Part 1 参考:Part 2
- 【358】GitHub 上面文件夹下载方法
参考:https://www.bilibili.com/read/cv210500/ 参考:https://www.jianshu.com/p/743ecc20ffb2 软件下载:Downloads ...
- easyUi onLoadSuccess:、onChange这些事件不能嵌套使用!!!!
easyUi onLoadSuccess:.onChange这些事件不能嵌套使用!!!!
- Swift的UILabel的一些属性
let label = UILabel(frame: CGRectMake(,,,)) label.backgroundColor = UIColor.redColor() label.text = ...
- 吴裕雄 python深度学习与实践(6)
from pylab import * import pandas as pd import matplotlib.pyplot as plot import numpy as np filePath ...
- The APK failed to install. Error:Could not parse error string.
问题一: The APK failed to install. Error:Could not parse error string. 今天拖拽自己的apk到模拟器上运行,报上述错误. 搜索解决方案. ...
- Spring 7种事务传播行为
1.PROPAGATION_REQUIRED:如果当前没有事务,就创建一个新事务,如果当前存在事务,就加入该事务,该设置是最常用的设置. 2.PROPAGATION_SUPPORTS:支持当前事务,如 ...
- msf客户端渗透(十):社会工程学
启动社会工程学攻击组件 生成二维码攻击模块 输入你想生成二维码的url,这里做演示用www.baidu.com 二维码生成后,在这个路径下 生成u盘,DVD的多媒体攻击载荷 通过修改autorun.i ...
- rsync+inotify实现数据实时同步
rsync rsync是linux系统下的数据镜像备份工具.支持远程同步,本地复制,或者与其他SSH.rsync主机同步. 优点: 1).可以镜像保存整个目录树和文件系统.保存源目录整个目录树和文件系 ...
- 修改.net反编译的dll
用.Net reflector 打开,配合reflexil工具. 有两种修改方法. 1.重写,试过,但不好用. 2.修改IL指令 一般只需修改简单的if判断. 方法:找到需要修改的行,把brfalse ...


- 这里涉及到真实值(true-),标称值(nominal-),和误差状态值(error-state)三个量,真实值是有标称值和误差值组合而来。标称值是有非线性方程而来的"大信号",误差值的线性方程而来满足线性高斯滤波的“小信号”。
2.1连续时间的IMU系统动态方程
2.1.1相关变量
- 这里的相关变量中,输入值是IMU的测量值am,bm" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">am,bm,以及当地重力加速度g" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">g;其他真值值变量的值都是由他们而来。其中normal值是一个抽象变量,表示理想值,是无法估计的。在融合中我们使用估计的真实值做为预测。
- 标称值是完全理想值,我们把各种因素产生的真实值和标称值的不确定性归于变量δx" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">δx表示。
- 这里采用Hamilton 四元数的表述方法
- 这里的角速率w" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">w使用的是locally的表述,这样可以直接使用机体系b下的传感器测量值wm" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">wm。
- 这里的角度误差δθ" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">δθ使用的也是locally的表述,这是很多文献和算法采用的经典方式,不过有证明说采用globally的方式定义的角度误差有更好的性质。
- 这里的加速度a" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">a定义的是globally,我的理解是,方便计算导航系下的速度和位置。

2.1.2真实状态运动方程(true-state kinematics equations )
- true-state 变量表示的运动方程.IMU bias的噪声定义为随机游走。
由于初始状态姿态未知,这种不确定即重力加速度向量的不确定,但是实际工程中我们是制定初始状态的,即重力加速度不确定不再存在,这里的方程也认为其为恒定值。
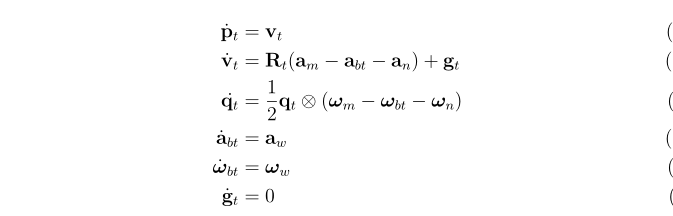
IMU误差来源分为两种,内部biasabt,wbt" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">abt,wbt和测量噪声an,wn" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">an,wn.
这里的IMU真实值是没有bias和测量噪声的值,IMU加速度计测量加速度不包含重力加速度,即如果自由落体运动,不考虑噪声加速度计的读数是0。
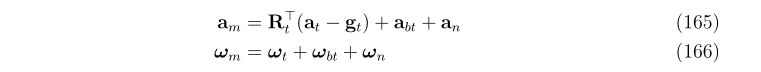
利用IMU测量代替真实值的系统真实状态运动方程x˙=ft(xt,u,w)" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">x˙=ft(xt,u,w),该方程状态为xt" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">xt,由IMU的含噪声测量值um" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">um驱动,并受高斯白噪声w" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">w干扰.
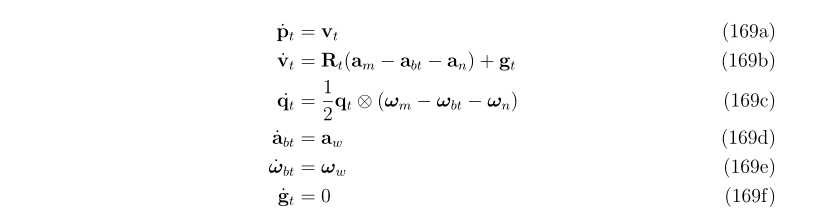
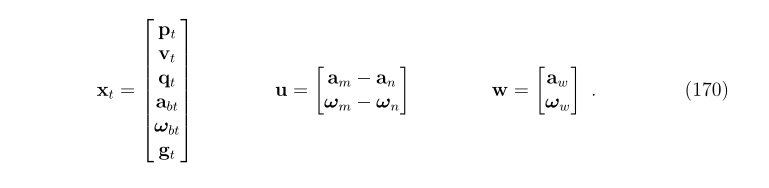
2.1.3标称状态运动方程(normal-state kinematics equations )
- 标称状态对应系统没有噪声和扰动的情况。
- 可以这么理解,标称值是把测量值am,wm" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">am,wm和bias当做理想值计算出来的理想状态;而实际值是在考虑测量值和bias有一部分应该不是我们想要的信号,是测量值减去噪声和bias减去扰动计算得到的。我们的目的是优化两者的误差,误差越小,测量值和bias包含的不确定性就越小。
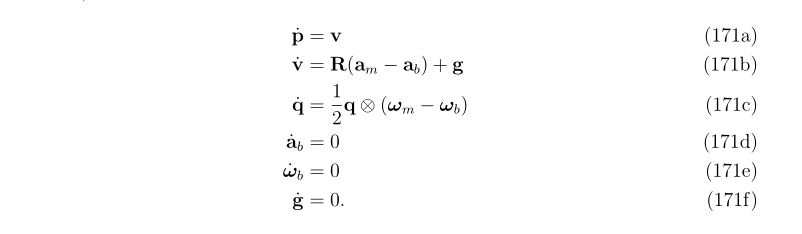
2.1.4误差状态运动方程
方程的右边变量是标称状态、IMU测量值和噪声项。
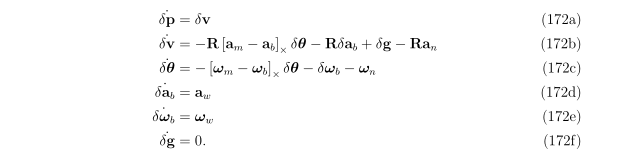
其中速度误差和角度误差推导如下,主要技巧是省略小量的二次以上的项以及真实值和标称值之间的数学关系。还有就是高斯噪声的各向同性,使旋转对其没有影响。


2.2离散时间的IMU系统动态方程
2.2.1离散时间的IMU系统动态方程
误差状态运动方程的离散化主要是利用其微分方程进行积分,并将其表示为迭代形式。积分的方法有很多种。
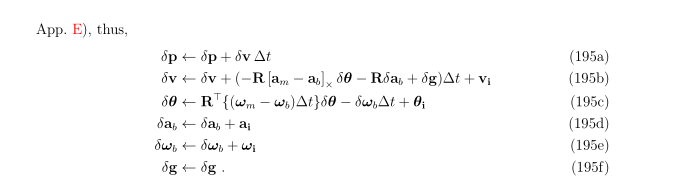
离散化后的噪声和连续状态的噪声存在差别,详细见IMU Noise Model.

2.2.2误差状态的雅克比矩阵和扰动矩阵
- 通过观察2.2.1很容易得到误差状态迭代方程的的雅克比矩阵;这里给出的是离散迭代方程的雅克比,和连续情况下误差状态的微分方程的雅克比,会有些不同。
- 这里的雅克比矩阵其实就是误差状态方程的状态转移矩阵。
- 这里的雅克比矩阵来源于真实状态运动方程的离散化,即2.2.4误差状态运动方程的推导过程即是其离散化的过程。


3.ESKF:Error state Kalman filter
3.1总体介绍
- 这里介绍sola的ESKF,其中的误差来源是IMU加速度计和陀螺仪读数噪声以及bias带的扰动。首先推导了IMU的系统误差动态方程,由于IMU造成的航位推算系统(DR:dead-reckoning position system)会随着时间漂移(我的理解是由于在只有IMU作为测量传感器的位姿测量系统里,航向角和位置都是靠积分得到的,因而会有航位的漂移问题)。所以将该方程做为KF的预测值,使用其他来源的数据如GPS或视觉作为矫正,构成融合数据的KF。
- 我的理解,作者这里提出的ESKF,和EKF其实是一回事。
3.2ESKF vs KF
- 作者比较了ESKF相对于KF的优点,有些不是完全理解
- 避免参数冗余,由于ESKF的参数和自由度一致,可以避免协方差矩阵的奇异性问题。
- ESKF的(误差)变量操作一直在原点附近(误差变量的值很小),可以避免可能地参数奇异性、万向节锁的问题,保证线性化的有效性。
- 误差状态值一致很小,意味着公式中误差的二次以乘积都可以忽略,使得相应的雅克比矩阵比较简单,提高计算速度。
- 可以让KF的correction速度低于prediction,这点不是很理解,贴在这里吧。

3.3fusing IMU with other complementary sensory data
3.3.1ESKF prediction
- 具体变量定义见2.3.2,在2.2.3中,我们使用IMU含噪声的测量值和bias去计算标称值。并且没有考虑测量值的噪声项和扰动,从而产生了误差。我们把所有不确定性引来的误差放在误差变量δx" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">δx中考虑,我们利用IMU测量值和高斯噪声去计算误差项,并将其作为ESKF的观测,并利用其它来源的数据如GPS,视觉等来作为矫正(使误差可观)。
- 这里用IMU作为观测,不是完全理解,我现在的理解是,IMU数据的引入使得预测项更加接近真实情况,参考《最优状态估计》,这里的IMU数据即运动方程里的控制项,如果没有测量值做控制项,我们需要进行比较强的假设,如恒速模型等;但是有了传感器数据作为控制输入,运动方程的模型就更加接近真实情况,有时我们也用里程计作为控制输入,但相对于IMU,里程计的测量位置误差会比较大(齿轮啮合不理想等),而且对于飞行器来说,里程计是不能用的。
- 最后我们利用上次的状态值、控制输入、传递的误差项来预测下一时刻的状态。
- 预测阶段均值和方差的更新公式:

3.3.2ESKF correction
3.2.1 通过correction建立误差的观测
这里使用另外的GPS或camera建立测量方程,并将观测方程在标称点附近进行线性化。

这里的雅克比矩阵推导使用了链式法则。


3.2.2 将观测误差注入标称状态
- 这样做使得这次迭代标称状态和真实状态相等,误差重置为0;

3.2.3ESKF reset
重置的过程主要涉及到不确定性即方差的传播,通常这里的雅克比可以近似为I。

这里的雅克比矩阵的推导

3.4 使用global angular errors的ESKF
- 之前有提到使用global angular error有更好的特性,这里进行相关的推导,所以涉及到的旋转积分要采用globally的左扰动。
- 这里的角速度仍使用locally,考虑到测量值是在机体系下表示的
3.4.1 连续时间误差状态运动方程

- 相关推导和locally相似,在角度误差微分方程推导里,四元数微分用的是locally,四元数积分用的是globally,这样做的可行性在于角度误差和角速率没有耦合在两者中使用。


3.4.2 离散误差状态运动方程

3.4.3 globally ESKF vs locally ESKF

四元数运动学笔记(5)IMU驱动的运动误差方程的更多相关文章
- 从零开始一起学习SLAM | 用四元数插值来对齐IMU和图像帧
视觉 Vs. IMU 小白:师兄,好久没见到你了啊,我最近在看IMU(Inertial Measurement Unit,惯性导航单元)相关的东西,正好有问题求助啊 师兄:又遇到啥问题啦? 小白:是这 ...
- input子系统学习笔记六 按键驱动实例分析下【转】
转自:http://blog.chinaunix.net/uid-20776117-id-3212095.html 本文接着input子系统学习笔记五 按键驱动实例分析上接续分析这个按键驱动实例! i ...
- AM335x(TQ335x)学习笔记——GPIO关键驱动移植
或按照S5PV210学习秩序.我们首先解决的关键问题.TQ335x有六个用户按钮,每个上.下.剩下.对.Enter和ESC. 我想开始学习S5PV210当同一,写输入子系统驱动器的关键问题要解决,但浏 ...
- AM335x(TQ335x)学习笔记——GPIO按键驱动移植
还是按照S5PV210的学习顺序来,我们首先解决按键问题.TQ335x有六个用户按键,分别是上.下.左.右.Enter和ESC.开始我想到的是跟学习S5PV210时一样,编写输入子系统驱动解决按键问题 ...
- MongoDB学习笔记~关于官方驱动集成IQueryable之后的一些事
回到目录 关于官方驱动集成IQueryable之后的一些事,有好事也有坏事,好事就是它会将你的linq语句非常友好的翻译成MongoDB语句,而坏事就是有一些linq语句不会被翻译,不会被翻译的代价就 ...
- Linux 驱动学习笔记05--字符驱动实例,实现一个共享内存设备的驱动
断断续续学驱动,好不容易有空,做了段字符驱动的例子.主要还是跟书上学习在此记录下来,以后说不定能回过头来温故知新. 首先上驱动源码 gmem.c: /************************* ...
- linux 驱动学习笔记04--简单驱动
首先贴代码helloworld.c和Makefile /************************************************************************ ...
- Yocto开发笔记之《驱动调试-华为3G模块》(QQ交流群:519230208)
QQ群:519230208,为避免广告骚扰,申请时请注明 “开发者” 字样 ======================================================== 参考:ht ...
- AM335x(TQ335x)学习笔记——Nand&&网卡驱动移植
移植完成声卡驱动之后本想再接再励,移植网卡驱动,但没想到的是TI维护的内核太健壮,移植网卡驱动跟之前移植按键驱动一样简单,Nand驱动也是如此,于是,本人将Nand和网卡放在同一篇文章中介绍.介绍之前 ...
随机推荐
- 【379】pandas 说明
参考:Part 1 参考:Part 2
- 【358】GitHub 上面文件夹下载方法
参考:https://www.bilibili.com/read/cv210500/ 参考:https://www.jianshu.com/p/743ecc20ffb2 软件下载:Downloads ...
- easyUi onLoadSuccess:、onChange这些事件不能嵌套使用!!!!
easyUi onLoadSuccess:.onChange这些事件不能嵌套使用!!!!
- Swift的UILabel的一些属性
let label = UILabel(frame: CGRectMake(,,,)) label.backgroundColor = UIColor.redColor() label.text = ...
- 吴裕雄 python深度学习与实践(6)
from pylab import * import pandas as pd import matplotlib.pyplot as plot import numpy as np filePath ...
- The APK failed to install. Error:Could not parse error string.
问题一: The APK failed to install. Error:Could not parse error string. 今天拖拽自己的apk到模拟器上运行,报上述错误. 搜索解决方案. ...
- Spring 7种事务传播行为
1.PROPAGATION_REQUIRED:如果当前没有事务,就创建一个新事务,如果当前存在事务,就加入该事务,该设置是最常用的设置. 2.PROPAGATION_SUPPORTS:支持当前事务,如 ...
- msf客户端渗透(十):社会工程学
启动社会工程学攻击组件 生成二维码攻击模块 输入你想生成二维码的url,这里做演示用www.baidu.com 二维码生成后,在这个路径下 生成u盘,DVD的多媒体攻击载荷 通过修改autorun.i ...
- rsync+inotify实现数据实时同步
rsync rsync是linux系统下的数据镜像备份工具.支持远程同步,本地复制,或者与其他SSH.rsync主机同步. 优点: 1).可以镜像保存整个目录树和文件系统.保存源目录整个目录树和文件系 ...
- 修改.net反编译的dll
用.Net reflector 打开,配合reflexil工具. 有两种修改方法. 1.重写,试过,但不好用. 2.修改IL指令 一般只需修改简单的if判断. 方法:找到需要修改的行,把brfalse ...
这里使用另外的GPS或camera建立测量方程,并将观测方程在标称点附近进行线性化。
这里的雅克比矩阵推导使用了链式法则。
重置的过程主要涉及到不确定性即方差的传播,通常这里的雅克比可以近似为I。
这里的雅克比矩阵的推导



视觉 Vs. IMU 小白:师兄,好久没见到你了啊,我最近在看IMU(Inertial Measurement Unit,惯性导航单元)相关的东西,正好有问题求助啊 师兄:又遇到啥问题啦? 小白:是这 ...
转自:http://blog.chinaunix.net/uid-20776117-id-3212095.html 本文接着input子系统学习笔记五 按键驱动实例分析上接续分析这个按键驱动实例! i ...
或按照S5PV210学习秩序.我们首先解决的关键问题.TQ335x有六个用户按钮,每个上.下.剩下.对.Enter和ESC. 我想开始学习S5PV210当同一,写输入子系统驱动器的关键问题要解决,但浏 ...
还是按照S5PV210的学习顺序来,我们首先解决按键问题.TQ335x有六个用户按键,分别是上.下.左.右.Enter和ESC.开始我想到的是跟学习S5PV210时一样,编写输入子系统驱动解决按键问题 ...
回到目录 关于官方驱动集成IQueryable之后的一些事,有好事也有坏事,好事就是它会将你的linq语句非常友好的翻译成MongoDB语句,而坏事就是有一些linq语句不会被翻译,不会被翻译的代价就 ...
断断续续学驱动,好不容易有空,做了段字符驱动的例子.主要还是跟书上学习在此记录下来,以后说不定能回过头来温故知新. 首先上驱动源码 gmem.c: /************************* ...
首先贴代码helloworld.c和Makefile /************************************************************************ ...
QQ群:519230208,为避免广告骚扰,申请时请注明 “开发者” 字样 ======================================================== 参考:ht ...
移植完成声卡驱动之后本想再接再励,移植网卡驱动,但没想到的是TI维护的内核太健壮,移植网卡驱动跟之前移植按键驱动一样简单,Nand驱动也是如此,于是,本人将Nand和网卡放在同一篇文章中介绍.介绍之前 ...
参考:Part 1 参考:Part 2
参考:https://www.bilibili.com/read/cv210500/ 参考:https://www.jianshu.com/p/743ecc20ffb2 软件下载:Downloads ...
easyUi onLoadSuccess:.onChange这些事件不能嵌套使用!!!!
let label = UILabel(frame: CGRectMake(,,,)) label.backgroundColor = UIColor.redColor() label.text = ...
from pylab import * import pandas as pd import matplotlib.pyplot as plot import numpy as np filePath ...
问题一: The APK failed to install. Error:Could not parse error string. 今天拖拽自己的apk到模拟器上运行,报上述错误. 搜索解决方案. ...
1.PROPAGATION_REQUIRED:如果当前没有事务,就创建一个新事务,如果当前存在事务,就加入该事务,该设置是最常用的设置. 2.PROPAGATION_SUPPORTS:支持当前事务,如 ...
启动社会工程学攻击组件 生成二维码攻击模块 输入你想生成二维码的url,这里做演示用www.baidu.com 二维码生成后,在这个路径下 生成u盘,DVD的多媒体攻击载荷 通过修改autorun.i ...
rsync rsync是linux系统下的数据镜像备份工具.支持远程同步,本地复制,或者与其他SSH.rsync主机同步. 优点: 1).可以镜像保存整个目录树和文件系统.保存源目录整个目录树和文件系 ...
用.Net reflector 打开,配合reflexil工具. 有两种修改方法. 1.重写,试过,但不好用. 2.修改IL指令 一般只需修改简单的if判断. 方法:找到需要修改的行,把brfalse ...
