EM算法原理详解
1.引言
以前我们讨论的概率模型都是只含观测变量(observable variable), 即这些变量都是可以观测出来的,那么给定数据,可以直接使用极大似然估计的方法或者贝叶斯估计的方法;但是当模型含有隐变量(latent variable)的时候, 就不能简单地使用这些估计方法。
如在高斯混合和EM算法中讨论的高斯混合就是典型的含有隐变量的例子,已经给出EM算法在高斯混合模型中的运用,下面我们来讨论一些原理性的东西。
2.Jensen 不等式
令 是值域为实数的函数,那么如果
是值域为实数的函数,那么如果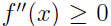 ,则
,则 就是一个凸函数,如果自变量 x 是向量, 那么当函数的海森矩阵
就是一个凸函数,如果自变量 x 是向量, 那么当函数的海森矩阵 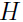 是半正定时(
是半正定时( ),
),  是凸函数,这是函数为凸函数的条件在向量输入时的泛化。
是凸函数,这是函数为凸函数的条件在向量输入时的泛化。
如果 ,则称
,则称 是严格凸函数,对应的向量输入时的泛化是
是严格凸函数,对应的向量输入时的泛化是 .
.
定理 令
是一个凸函数,令
是一个随机变量,那么
当 时严格凸函数的时,当且仅当
时严格凸函数的时,当且仅当 以概率 1 成立的时,
以概率 1 成立的时, . 即当
. 即当 时常量时,上面不等式的等号成立。
时常量时,上面不等式的等号成立。
注意上面 E 是表示期望的意思,习惯上,在写变量期望的时候,会把紧跟括号略去,即 .
.
用下面的图对上面的定理作一个解释:

这个图中的实线代表凸函数 , 随机变量
, 随机变量 有 0.5 的概率取 a, 同样以 0.5 的概率取 b, 所以
有 0.5 的概率取 a, 同样以 0.5 的概率取 b, 所以 的期望位于a,b的正中间,即a,b的均值.
的期望位于a,b的正中间,即a,b的均值.
从图中可以看出,在 y 轴上, 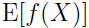 位于
位于 之间,因为
之间,因为 是凸函数,则必如上图所示,
是凸函数,则必如上图所示,
所以很多情况下,许多人并去记忆这个不等式,而是记住上面的图,这样更容易理解。
注意:如果 是(严格)凹函数,即
是(严格)凹函数,即 使(严格)凸函数(即,
使(严格)凸函数(即,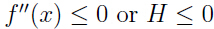 ),那么Jensen不等式照样成立,只不过不等号方向相反:
),那么Jensen不等式照样成立,只不过不等号方向相反: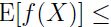

3.EM算法
假设在一个估计问题中有m个独立样本 ,根据这些数据,希望拟合出模型
,根据这些数据,希望拟合出模型 的参数,那么对数似然函数:
的参数,那么对数似然函数:

这里, 是隐变量,如果
是隐变量,如果 能够被观测出来,最大似然估计就会变得很容易,但是现在
能够被观测出来,最大似然估计就会变得很容易,但是现在 观测不出来,是隐变量。
观测不出来,是隐变量。
在这种情况下,EM算法给出了一种很有效的最大似然估计的方法:重复地构造 的下界(E步),然后最大化这个下界(M步)。
的下界(E步),然后最大化这个下界(M步)。
对于每个 ,令
,令 表示隐变量
表示隐变量 的分布,即
的分布,即
 ,考虑:
,考虑:

由(2)到(3)的推导用到了上面的Jensen不等式,此时
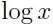 是一个凹函数,因为
是一个凹函数,因为 ,考虑上面关于
,考虑上面关于 的分布
的分布 ,
,

正好是数量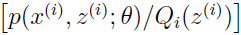 的期望,由Jensen不等式可以得到:
的期望,由Jensen不等式可以得到:
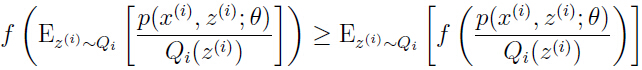
由此可以从(2)推出(3).
但是由于隐变量的存在,直接最大化 很困难!试想如果能让
很困难!试想如果能让 直接与它的下界相等,那么任何可以使
直接与它的下界相等,那么任何可以使 的下界增大的
的下界增大的 ,也可以使
,也可以使 增大,所以自然就是选择出使
增大,所以自然就是选择出使 的下界达到极大的参数
的下界达到极大的参数 .
.
怎么样才能使得 取得下界呢,即上面不等式取等号,关键在于隐变量
取得下界呢,即上面不等式取等号,关键在于隐变量 如何处理,下面就此讨论。
如何处理,下面就此讨论。
现在,对于任意的分布 ,(3)给出了似然函数
,(3)给出了似然函数 的下界. 对于分布
的下界. 对于分布 到底是什么分布,可以有很多种选择,到底该选择哪一种呢?
到底是什么分布,可以有很多种选择,到底该选择哪一种呢?
在上面讨论Jensen不等式的时候可以看出,不等式中等号成立的条件是随机变量变成“常量”,对于 要想取得下界值,必须要求
要想取得下界值,必须要求

其中常数 c 与变量 无关,这很容易做到,我们选择分布
无关,这很容易做到,我们选择分布 的时候,满足下面的条件即可:
的时候,满足下面的条件即可:

由于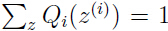 ,于是我们可以知道:
,于是我们可以知道:

注意理解上面这个等式式子是如何得出来的!!
于是就可以把分布 设定为:在参数
设定为:在参数 下,给定
下,给定 后,
后, 的后验分布。
的后验分布。
这样设定好隐变量的分布 之后,
之后, 就直接取其下界,原来最大化似然函数
就直接取其下界,原来最大化似然函数 的问题转换为最大化其下界,这就是E步!
的问题转换为最大化其下界,这就是E步!
在M步中,就是去调整参数 最大化上面提到的式子(3).
最大化上面提到的式子(3).
不断重复E步和M步就是EM算法:
重复迭代直至收敛{

}
我们如何知道算法收敛呢?
假如 和
和 是两次连续迭代后的参数,需要证明
是两次连续迭代后的参数,需要证明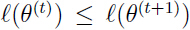 .
.
正如上面所述,由于我们再选择分布 时,选择:
时,选择: ,于是:
,于是:

参数 就是通过极大化上面右边的式子得出,因此:
就是通过极大化上面右边的式子得出,因此:

注意第不等式(4)来自于:

这个式子对于任意的 和
和 都成立,当然对于
都成立,当然对于 和
和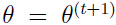 也成立。对于不等式(5),因为
也成立。对于不等式(5),因为 是通过如下极大化过程选出来的:
是通过如下极大化过程选出来的:

所以在 处,式子的值要比在
处,式子的值要比在 处式子的值要大!
处式子的值要大!
式子(6)是通过上面讨论过的方法选择出合适的 使得Jensen不等式取等号!
使得Jensen不等式取等号!
因此,EM算法使得似然函数单调收敛。在上面描述EM算法的时候,说是“重复迭代直至收敛”,一个常用的检查收敛的方法是:如果两次连续迭代之后,似然函数 的值变化很小(在某个可容忍的范围内),就EM算法中
的值变化很小(在某个可容忍的范围内),就EM算法中 的变化已经很慢,可以停止迭代了。
的变化已经很慢,可以停止迭代了。
注意:如果定义:

从之前的推导,我们知道 . EM算法看作是关于函数 J 的梯度上升:E步是关于参数Q,M步是关于参数
. EM算法看作是关于函数 J 的梯度上升:E步是关于参数Q,M步是关于参数 .
.
4.高斯混合的修正
在 高斯混合和EM算法 中,我们将EM算法用于优化求解高斯混合模型,拟合参数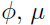 和
和 .
.
E步:

这里 表示的是在分布
表示的是在分布 下,
下, 取
取 的概率。
的概率。
M步:考虑参数 ,最大化数值:
,最大化数值:

最大化求 ,对上面的式子关于
,对上面的式子关于 求偏导数:
求偏导数:

令这个偏导数为0,求出 的更新方式:
的更新方式:
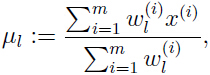
这是在 高斯混合和EM算法 中已经得出的结论。
再考虑如何更新参数 ,把只与
,把只与 有关的项写出来,发现只需要最大化:
有关的项写出来,发现只需要最大化:

因为, ,所有
,所有 的和为1,所以这是一个约束优化问题,参考简易解说拉格朗日对偶(Lagrange duality),构造拉格朗日函数:
的和为1,所以这是一个约束优化问题,参考简易解说拉格朗日对偶(Lagrange duality),构造拉格朗日函数:

其中 β 是拉格朗日乘子. 求偏导数:
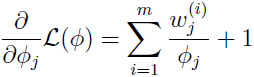
令偏导数为0,得到:

即: 利用约束条件:
利用约束条件: ,得到:
,得到: (注意这里用到:
(注意这里用到: ).
).
于是可以得到参数 的更新规则:
的更新规则:

关于参数 的更新规则,以及整个EM算法如何运用到高斯混合模型的优化,请参考:高斯混合和EM算法!
的更新规则,以及整个EM算法如何运用到高斯混合模型的优化,请参考:高斯混合和EM算法!
5.总结
所谓EM算法就是在含有隐变量的时候,把隐变量的分布设定为一个以观测变量为前提条件的后验分布,使得参数的似然函数与其下界相等,通过极大化这个下界来极大化似然函数,从避免直接极大化似然函数过程中因为隐变量未知而带来的困难!EM算法主要是两步,E步选择出合适的隐变量分布(一个以观测变量为前提条件的后验分布),使得参数的似然函数与其下界相等;M步:极大化似然函数的下界,拟合出参数.
EM算法原理详解的更多相关文章
- 2. EM算法-原理详解
1. EM算法-数学基础 2. EM算法-原理详解 3. EM算法-高斯混合模型GMM 4. EM算法-高斯混合模型GMM详细代码实现 5. EM算法-高斯混合模型GMM+Lasso 1. 前言 概率 ...
- CRF(条件随机场)与Viterbi(维特比)算法原理详解
摘自:https://mp.weixin.qq.com/s/GXbFxlExDtjtQe-OPwfokA https://www.cnblogs.com/zhibei/p/9391014.html C ...
- [置顶]
Isolation Forest算法原理详解
本文只介绍原论文中的 Isolation Forest 孤立点检测算法的原理,实际的代码实现详解请参照我的另一篇博客:Isolation Forest算法实现详解. 或者读者可以到我的GitHub上去 ...
- DQN算法原理详解
一. 概述 强化学习算法可以分为三大类:value based, policy based 和 actor critic. 常见的是以DQN为代表的value based算法,这种算法中只有一个值函数 ...
- AAC解码算法原理详解
”
- 网络最大流问题之Ford-Fulkerson算法原理详解
前言 最大流问题是网络优化中典型的问题,用形象的语言来描述就是在满足容量约束的前提下将尽可能多的流从源节点(始点)到汇节点(终点).解决此问题的经典方法很多,本文介绍广为人熟知的Ford-Fulker ...
- hash算法原理详解
转载出处http://blog.csdn.net/tanggao1314/article/details/51457585 一.概念 哈希表就是一种以 键-值(key-indexed) 存储数据的结构 ...
- [置顶]
Isolation Forest算法实现详解
本文算法完整实现源码已开源至本人的GitHub(如果对你有帮助,请给一个 star ),参看其中的 iforest 包下的 IForest 和 ITree 两个类: https://github.co ...
- Isolation Forest算法实现详解
本文介绍的 Isolation Forest 算法原理请参看我的博客:Isolation Forest异常检测算法原理详解,本文中我们只介绍详细的代码实现过程. 1.ITree的设计与实现 首先,我们 ...
随机推荐
- springboot项目的创建
创建springboot项目 包名和项目名 选择需要使用的框架,web 然后再点击下一步,完成即可创建springboot项目
- Spring源码学习:DefaultAopProxyFactory
/* * Copyright 2002-2015 the original author or authors. * * Licensed under the Apache License, Vers ...
- 冒泡排序的C、C++实现
一.冒泡排序 冒泡排序就是重复地走访过要排序的元素列,依次比较两个相邻的元素,如果他们的顺序(如数字从大到小.首字母从A到Z)错误就把他们交换过来.走访元素的工作是重复地进行直到没有相邻元素需要交换, ...
- java之不修改变量的数据类型的处理方式
- [代码]--给GridControl中的某列添加图片
要让GridControl的某列显示图片只需要数据源中有图片就可以正确显示 1.给DataSet添加一列,格式为image ds.Tables[].Columns.Add("SIGN&quo ...
- String args[] 和 String[] args 有什么区别
String args[] 和 String[] args 有什么区别 public static void main(String args[]) 或 public static void main ...
- KUR-Couriers
题目链接: QwQ Solution: 以权值为下标,对每个点建树 对于x点,以它为根的树涵盖的是1到x区间内每个数出现的次数 Code: #include<bits/stdc++.h> ...
- 【Revit API】FamilyInstance、FamilySymbol、Family的寻找关系
话不多说,做个笔记 FamilyInstance instance; var typeid = instance.GetTypeId(); var symbol = RevitDoc.GetEleme ...
- 学习5_STM32--外设通信方式
就拿stm32的外设spi来说,通信方式主要有3种 > spi常规收发方式 (在轮询机制下通过判断缓冲区空与非空作为收发依据) > spi中断收发方式 (在中断机制下收发数据 ...
- luogu1373 小a和uim之大逃离 (dp)
直接设f[i][j][k][l][2]是在(i,j)时两人分数是k,l,复杂度会爆掉 但其实只需要知道两人分数只差就行了 所以设f[i][j][k][2],k是分数之差%(K+1),最后一位表示该谁走 ...
