exgcd模板
逆元模板P1082
#include <cstdio>
#include <algorithm> int exgcd(int a, int b, int &x, int &y) {
if(!b) {
x = ;
y = ;
return a;
}
int g = exgcd(b, a % b, x, y);
std::swap(x, y);
y -= (a / b) * x;
return g;
} int main() {
int a, b;
scanf("%d%d", &a, &b);
int x, y;
exgcd(a, b, x, y);
x = (x % b + b) % b;
printf("%d", x);
return ;
}
exgcd
注意exgcd不仅可以求解ax+by=gcd,还可以直接求解
ax+by=c(gcd|c)
代码:
LL Val;
LL mygcd(LL a, LL b, LL &x, LL &y) {
if(!b) {
x = Val / a;
y = ;
return a;
}
LL g = mygcd(b, a % b, x, y);
std::swap(x, y);
y -= (a / b) * x;
return g;
}
mygcd
但是有个缺点,就是跟上面比起来可能会爆long long而出错(屠龙勇士)
关于exgcd的推导过程:
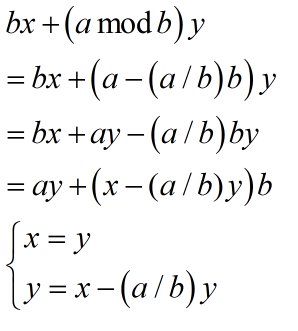
exgcd模板的更多相关文章
- poj 2115 C Looooops——exgcd模板
题目:http://poj.org/problem?id=2115 exgcd裸题.注意最后各种%b.注意打出正确的exgcd板子.就是别忘了/=g. #include<iostream> ...
- 扩展欧几里得(exgcd)与同余详解
exgcd入门以及同余基础 gcd,欧几里得的智慧结晶,信息竞赛的重要算法,数论的...(编不下去了 讲exgcd之前,我们先普及一下同余的性质: 若,那么 若,,且p1,p2互质, 有了这三个式子, ...
- 浅谈扩展欧几里得[exgcd] By cellur925
关于扩展欧几里得从寒假时就很迷,抄题解过了同余方程,但是原理并不理解. 今天终于把坑填上了qwq. 由于本人太菜,不会用markdown,所以这篇总结是手写的(什么).(字丑不要嫌弃嘛) ****** ...
- POJ 1061 青蛙的约会(扩展欧几里得)
根据题意,两个青蛙跳到同一个点上才算是遇到了,所以有 (x+m*t) - (y+n*t) = p * ll; (t是跳的次数,ll是a青蛙跳的圈数跟b青蛙的圈数之差.整个就是路程差等于纬度线周长的整 ...
- NOIP2012题解
NOIP2012题解 Day1 Vigenère 密码 vigenere 直接模拟就好了,对于那张表找找规律就很短了. #include<iostream> #include<cst ...
- POJ - 2115C Looooops 扩展欧几里得(做的少了无法一眼看出)
题目大意&&分析: for (variable = A; variable != B; variable += C) statement;这个循环式子表示a+c*n(n为整数)==b是 ...
- Noip前的大抱佛脚----Noip真题复习
Noip前的大抱佛脚----Noip真题复习 Tags: Noip前的大抱佛脚 Noip2010 题目不难,但是三个半小时的话要写四道题还是需要码力,不过按照现在的实力应该不出意外可以AK的. 机器翻 ...
- YBT 6 数学基础
$补+写题ing$ 第 1 章 快速幂 序列的第 k 个数 link $solution:$ 板子 A 的 B 次方 link $solution:$ 板子 [NOIP2013] 转圈游戏 link ...
- p1516&poj1061&bzoj1477 青蛙的约会
传送门(洛谷) 题目 两只青蛙在网上相识了,它们聊得很开心,于是觉得很有必要见一面.它们很高兴地发现它们住在同一条纬度线上,于是它们约定各自朝西跳,直到碰面为止.可是它们出发之前忘记了一件很重要的事情 ...
随机推荐
- 20155339 Exp4 恶意代码分析
20155339 Exp4 恶意代码分析 实验后回答问题 (1)如果在工作中怀疑一台主机上有恶意代码,但只是猜想,所有想监控下系统一天天的到底在干些什么.请设计下你想监控的操作有哪些,用什么方法来监控 ...
- controlfile 备份到trace文件例子
主要是为了学习oracle的克隆.参考: http://www.dba-oracle.com/oracle_tips_db_copy.htm 执行: SQL>alter database bac ...
- python 回溯法 子集树模板 系列 —— 6、排课问题
问题 某乡村小学有六个年级,每个年级有一个班,共六个班. 周一到周五,每天上6节课,共计30节课. 开设的课程 一年级:语(9)数(9)书(2)体(2)美(2)音(2)德(2)班(1)安(1) 二年级 ...
- Panorama——H5实现全景图片原理
前言 H5是怎么实现全景图片播放呢? 正文 全景图的基本原理即 "等距圆柱投影",这是一种将球体上的各个点投影到圆柱体的侧面上的一种投影方式,投影后再展开就是一张 2:1 的矩形图 ...
- 微信小程序初体验与DEMO分享
前言 前一段时间微信公布小程序,瞬间引来了大量的关注.博主的公司也将其定为目标之一,遂派本菜为先头兵(踩坑侠). 这次开发了一个比较完整的DEMO,模仿自某个APP首页,由于保护隐私的目的我把数据拷贝 ...
- (功能篇)回顾Bug管理系统Mantis优化改造经历
共分为两篇,功能篇和技术篇. 时间大约是2016年冬天. 考虑搭一个用于Bug管理和追踪的系统. 综合比较下,选择了小巧的开源工具,Mantis. 在源码基础上,做代码修改,完成了定制版的优化改造. ...
- 2018-07-09--记录一次gitlab迁移事件及遇到的问题
一.事情起因 因机房服务器即将到期,需要将即将到期的服务器迁移至云上,迁移之前没有查看老环境的Gitlab是什么版本,直接装的Gitlab社区版,做数据导入时提示版本错误: [root@vpn-ser ...
- 212. Space Replacement【LintCode by java】
Description Write a method to replace all spaces in a string with %20. The string is given in a char ...
- 如何基于 K8S 多租能力构建 Serverless Container
当前 Kubernetes 已经成为名副其实的企业级容器编排规范,很多云平台都开始提供兼容 Kubernetes 接口的容器服务.而在多用户支持方面,多数平台选择直接提供专属虚机集群,用户需要花费大量 ...
- 《Linux内核》课本读书笔记 第一章、第二章
