矩阵乘法&&矩阵快速幂&&最基本的矩阵模型——斐波那契数列

矩阵，一个神奇又令人崩溃的东西，常常用来优化序列递推

在百度百科中，矩阵的定义：

在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合 ，最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。

好，很高深对吧。那我们就更加直接地理解一下矩阵的实质：二维数组

好了这个SB都会，就不解释了

同二维数组一样，矩阵是一个'纵横排列的二维数据表格'，它一般是一个n*m的二维数组，其中n*m表示它有n行m列

每一位上的数可以用下标i,j来表示，形如这样一个矩阵：

这里我们就可以用B[1][2]来表示8这个元素

矩阵有加/减/乘法（有没有除法我不知道），其中加减法的限制比较大，当且仅当两个矩阵的行列数都相等时才能进行加减

加减的操作也很简单，只需要按位加减即可

这些都是次要的，最主要的其实是矩阵乘法

我们定义矩阵乘法：设A为m*p的矩阵，B为p*n的矩阵，那么称m*n的矩阵C为矩阵A与B的乘积，记作C=AB，其中矩阵C中的第i行第j列元素可以表示为：

这样我们就很轻松的得到了一个O(n^3)的矩阵乘法，虽然还有更快的，但一般来说已经足够

矩阵乘法有以下几条重要性质：

1. 矩阵乘法满足集合律，即(AB)C=A(BC)

2. 矩阵乘法满足分配律，即(A+B)C=AC+BC

3. 矩阵乘法一般不满足交换律

以上第三条就告诉我们，平时写两个数相乘的时候可以为所欲为，但是矩阵就完全不同了，AB!=BA

很简单，结合矩阵乘法来理解下。

换句更简单的，甚至交换后这两个矩阵都无法相乘，因为他们的列数可能就不相等了

然后我们又由于第一条可以得出矩阵快速幂的算法

首先矩阵幂只有方阵（即行数等于列数的矩阵）才可以做，要不然到后面都乘不了了（还是因为列数不相等了）

这个也很简单，我们只需要把一般的快速幂乘法部分改成矩阵乘法即可

还是一句话：不要乘反了！

对了，还要引出一个叫单位矩阵的东西，这个就好比一般乘法中的单位1一样。任何一个矩阵乘上单位矩阵都得到原来这个矩阵

单位矩阵为：

就是一个矩阵对角线上都是1

自己动手推一下就可以更深刻地理解一下了

然后我们就引出我们讨论的问题：斐波那契数列的矩阵优化

例题：Luogu P1962 斐波那契数列，求斐波那契数列的第n项%一个数的值

我们可以利用矩阵在线性代数和方程的作用在解决这个问题

我们考虑一个矩阵：

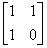
然后我们用一个列向量（就是列数为1的矩阵）来表示一下当前状态下斐波那契数列的值，由于斐波那契数列只要用到前两项，因此我们可以设：

然后我们让这两个矩阵相乘，得到新的矩阵：

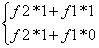
上面的这一项不就是斐波那契的递推式了吗？而且下面的这一项刚好可以为下一次做准备

因此我们只需要把原来的[1,1]列向量乘斐波那契的递推矩阵(n-2)次即可（注意前面的两项就是初始值）

但是如果就是这样的话就太慢了，因此我们又联想到矩阵乘法的结合律

即直接先求出斐波那契矩阵的(n-2)次，然后再与[1,1]的列向量相乘即可

再简化后就是斐波那契矩阵的(n-2)次的[1][1]与[1][2]上值的和

这样就完成了矩阵的第一步也是最简单，最基础的一步

注意矩阵一般的写法还是写成结构体比较好

由于这里的矩阵大小都是确定的，就没有在矩阵中记录行列数了，一般情况下都是以记录为主

好了接下来给出CODE

#include<cstdio>
using namespace std;
typedef long long LL;
const LL N=3,mod=1000000007;
LL F[N],ans[N];
struct Matrix
{
    LL a[N][N];
    inline void init(void)
    {
        a[1][1]=a[2][2]=1;
        a[1][2]=a[2][1]=0;
    }
    inline void Fb_init(void)
    {
        a[1][1]=a[1][2]=a[2][1]=1;
        a[2][2]=0;
    }
};
inline Matrix mul(Matrix A,Matrix B)
{
    register int i,j,k;
    Matrix C;
    for (i=1;i<N;++i)
    for (j=1;j<N;++j)
    for (C.a[i][j]=0,k=1;k<N;++k)
    C.a[i][j]=(C.a[i][j]+A.a[i][k]*B.a[k][j])%mod;
    return C;
}
inline Matrix quick_pow(Matrix A,LL p)
{
    Matrix B; B.init();
    while (p)
    {
        if (p%2) B=mul(B,A);
        A=mul(A,A); p/=2;
    }
    return B;
}
int main()
{
    register int i,j;
    LL n; scanf("%lld",&n);
    if (n<=2) { puts("1"); return 0; }
    n-=2; F[1]=F[2]=1;
    Matrix A; A.Fb_init();
    A=quick_pow(A,n);
    printf("%lld",(A.a[1][1]+A.a[1][2])%mod);
    return 0;
}

（以上的一部分图片来自百度百科，一部分来自于Luogu憧憬未来 dalao）的题解