Symbol Tables

符号表

符号表是键值对的集合，支持给定键查找值的操作，有很多应用：

API

put() 和 get() 是最基础的两个操作，为了保证代码的一致性，简洁性和实用性，先说下具体实现中的几个设计选择。

• 泛型 我们在考虑方法时不指定在处理的键和值的类型，而是使用泛型。

• 重复的键 每个键只对应一个值（表里没有重复的键），插入键值对的时候如果发现表里已经有这个键，那就更新该键值对的值。这些约定定义了关联数组（associative array）抽象，你可以把符号表想象成一个数组，其中键是索引而值是数组元素。

• 空值 不允许键对应的值为空（null）。直接原因是 get() 方法在表里没有相应传入的键时返回 null。这样约定，给定键我们还可以看符号表是否给它定义了值，看 get() 方法是否返回 null 就好。另外，方法 delete() 可以通过调用 put() 方法时在第二个参数传 null 来实现。

• 删除 符号表的删除操作一般有两种策略。一是懒删除（lazy deletion），即上面提到的直接用 put() 更新为 null，然后可能过会儿再移除这样的键。二是即时删除（eage deletion），马上把键从符号表中移除。在我们的符号表实现中不会使用默认方案，即不用 put(key, null)。

• 迭代 key() 返回一个迭代器给客户端遍历所有键。

• 键的等价性 Java 要求为每个对象实现一个 equals() 方法，本身也为标准类型如 Integer，Double 和 String 以及更复杂的类型如 Date，File 和 URL 实现了这个方法，我们以这个方法来确定一个给定的键是否在符号表中。在实际中，对自定义的键需要重写 equals() 方法，这在 part1-pa4 中有提过，可以参考 Date.java 和 Transaction.java，提下原来没讲到的 equals() 应实现一个等价关系，满足:

  • 自反性（Reflexive）：x.equals(x) 返回真。

  • 对称性（Symmetric）：若 x.equals(y) 为真，则 y.equals(x) 也为真。

  • 传递性（Transitive）：若 x.equals(y) 为真且 y.equals(z) 为真，那么 x.equals(z) 为真。

另外，equals() 的参数必须是一个对象，还要满足：

• 一致性（Consistency）：当两个对象都没有被修改时，多次调用 x.equals() 返回相同的值。

• 非空：x.equals(null) 返回 false。

最后，最好使用不可变的数据类型作为键，以此来保证符号表的一致性。

再蛮打一下符号表的测试用例，一个统计字符最近出现的位置，一个输出出现频率最高的字符串：

public static void main(String[] args) {
    ST<String, Integer> st = new ST<String, Integer>();
    for (int i = 0; !StdIn.isEmpty(); i++) {
        String key = StdIn.readString();
        st.put(key, i);
    }

    for (String s : st.keys()) {
        StdOut.println(s + " " + st.get(s));
    }
}

public class FrequencyCounter {
    public static void main(String[] args) {
        int minlen = Integer.parseInt(args[0]);
        ST<String, Integer> st = new ST<String, Integer>();
        while (!StdIn.isEmpty()) {
            String word = StdIn.readString();
            if (word.length() < minlen) continue;    // ignore short strings
            if (!st.contains(word)) st.put(word, 1);
            else st.put(word, st.get(word) + 1);
        }

        String max = "";
        st.put(max, 0);
        for (String word : st.keys()) {
            if (st.get(word) > st.get(max))
                max = word;
        }
        StdOut.println(max + " " + st.get(max));
    }
}

elementary implementations

符号表的一个简单实现是使用链表（无序），每个节点存储一个键值对。get() 方法遍历链表，用 equals() 方法匹配查找的键，成功则返回对应的值，失败则返回 null。put() 方法同样遍历链表，用 equals() 方法看表中是否已存在该键，存在则更新对应的值，不存在则新生成一个节点存在表头。这种方法，我们称为顺序查找（sequential search）。

示例图：

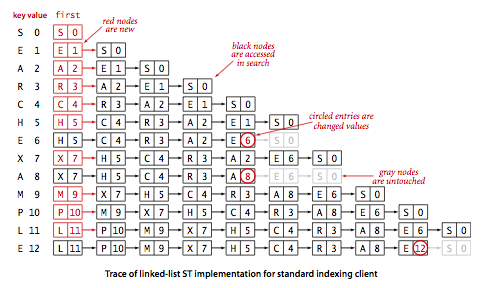
无序链表的顺序查找在最坏情况下，查找和插入的时间复杂度都是 N 级别的，平均情况下查找是 N/2 级别，但插入还是 N 级别。我们希望能找到更高效的实现，不管是查找还是插入，于是先来了解下有序（可比较类型，下面使用 compareTo() 方法）数组的二分查找。

实现的关键是 rank() 方法，它会返回符号表中比给定键值小的键的数目。对于 get() 来说，rank() 准确地告诉我们去哪找（找不到就不在表中）。对于 put() 来说，rank() 准确地告诉我们去哪更新表中存在的键的值，或是要把新的键值对放在哪。插入新键值对时，我们把较大的键都后移一位来腾出位置，以此来维护有序性。

插入图例：

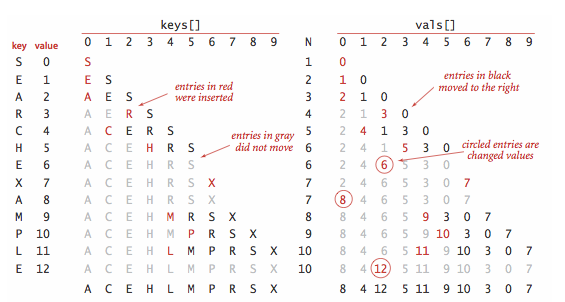
查找图例：

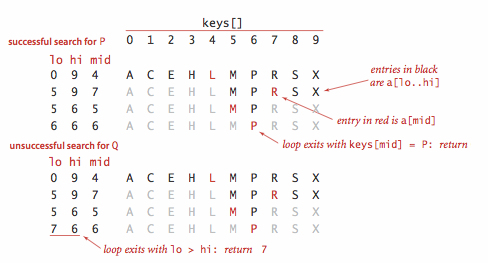
代码：

public void put(Key key, Value val) {
    int i = rank(key);
    // key is already in table
    if (i < N && keys[i].compareTo(key) == 0) {
        vals[i] = val;
        return;
    }
    // insert new key-value pair
    for (int j = N; j > i; j--) {
        keys[j] = keys[j--];
        vals[j] = vals[j--];
    }
    keys[i] = key;
    vals[i] = val;
    N++;
}

public Value get(Key key) {
    if (isEmpty()) return null;
    int i = rank(key);
    if (i < N && keys[i].compareTo(key) == 0) return vals[i];
    else return null;
}

private int rank(Key key) {
    int lo = 0, hi = N - 1;
    while (lo <= hi) {
        int mid = lo + (hi - lo) / 2;
        int cmp = key.compareTo(keys[mid]);
        if (cmp < 0) hi = mid - 1;
        else if (cmp > 0) lo = mid + 1;
        else return mid;
    }
    return lo;
}

这是简略版，完整的参见：BinarySearchST.java。

维护数组有序，就可以使用二分查找（上面的 rank() 方法）来大大减少比较的次数，和数组中间比完看在哪边再递归地处理，查找的复杂度最坏情况下也是 lgN 级别的。但最坏情况下，插入还是 N 级别，因为大的键都要后移，不过平均是 N/2 级别，比原来链表都是 N 高效。

ordered operations

有序数组里的键自然是可比较的，还有一些和顺序有关的便利的操作，API 如下：

这些操作还是很实用的，像下面的例子：

借助 rank() 方法，实现也比较简洁，如：

public Key ceiling(Key key) {
    int i = rank(key);
    return keys[i];
}

完整的参见：BinarySearchST.java。

综上，比较一下无序链表顺序查找和有序数组二分查找实现的符号表：

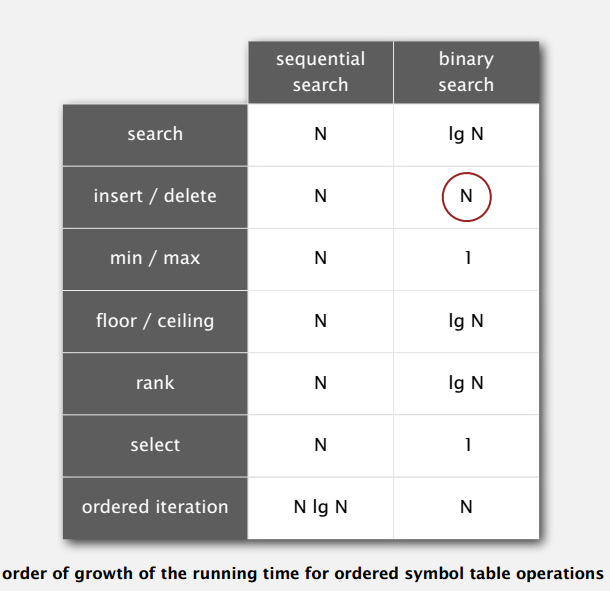
可见，二分查找的插入和删除还是有改进空间的。

BSTs

接着我们来了解一种更高效的符号表实现：二叉查找树，它结合了链表插入的灵活性和有序数组查找的快捷性，大概长这个样子：

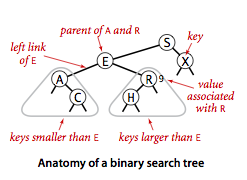
具有显式的树结构，每个节点有两个链接。其中键是可比较的，且键大于左子树小于右子树。所以每个节点包含四个部分，键，值以及指向左右子树的引用：

private class Node {
    private Key key;
    private Value val;
    private Node left, right;
    public Node(Key key, Value val) {
        this.key = key;
        this.val = val;
    }
}

键大于左子树小于右子树，查找的时候自然就是一个二分的过程。

查找代码：

public Value get(Key key) {
    Node x = root;
    while (x != null) {
        int cmp = key.compareTo(x.key);
        if (cmp < 0) x = x.left;
        else if (cmp > 0) x = x.right;
        else return x.val;
    }
    return null;
}

查找图例：

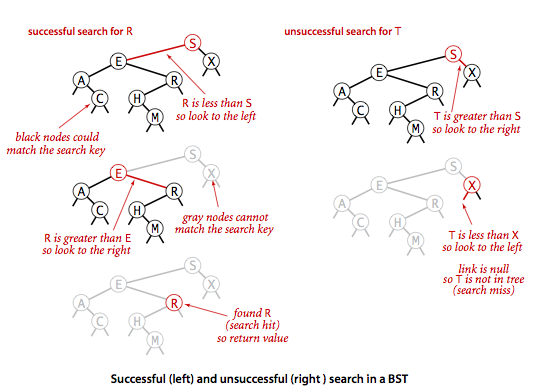
类似的，插入过程也是二分查找找到合适的位置。

插入代码：

public void put(Key key, Value val) {
    root = put(root, key, val);
}

private Node put(Node x, Key key, Value val) {
    if (x == null) return new Node(key, val);
    int cmp = key.compareTo(x.key);
    if (cmp < 0) x.left = put(x.left, key, val);
    else if (cmp > 0) x.right = put(x.right, key, val);
    else x.val = val;
    return x;
}

插入图例：

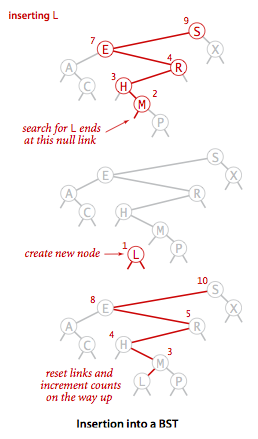
上面的查找和插入的复杂度显然和树高相关，但是！二叉查找树的形状和输入有关，不一定都长得很好看，最坏情况下树高为 N，那就退化成链表实现了。

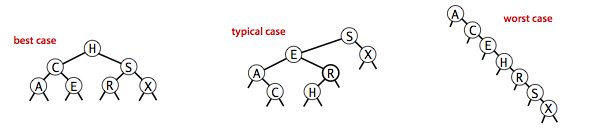
不过，其实二叉查找树和快排的划分过程存在对应关系：

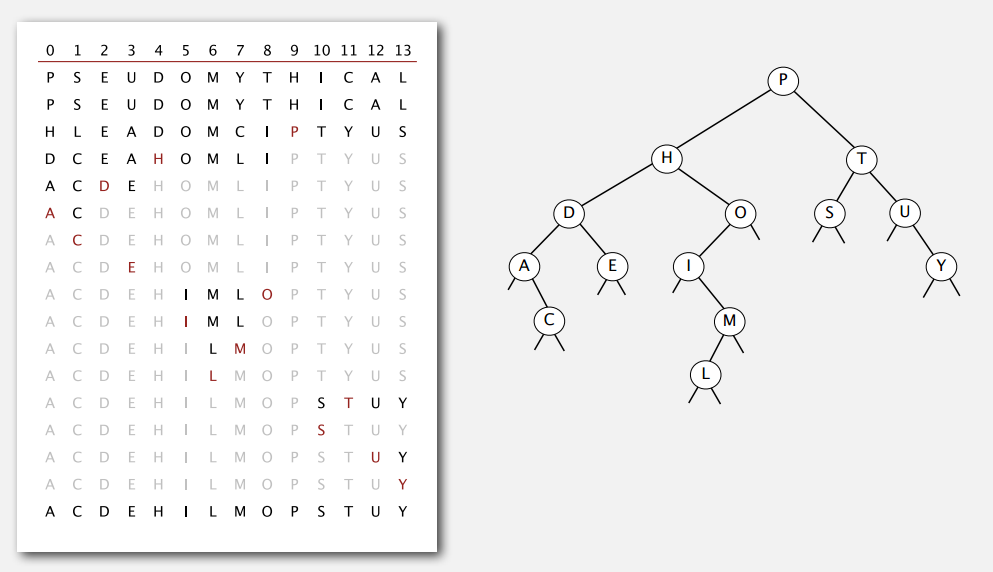
于是乎，借用快排的结论，如果是随机插入的话，那平均情况下复杂度也是 lgN 级别的。

bst ordered operations

再先来看看二叉搜索树中和顺序相关的操作怎么实现。

Minimum and maximum

如果根节点的左链接为空的话，那么根节点即为最小键；不然最小键就在左子树，把左孩子当做新的根节点来看，继续找下去。找最大键类似，不过是把左换成右。

Floor and ceiling

如果给定的键小于根节点的键，那么向下取整（floor）一定在左子树。如果大于根节点的键，那么 floor 有可能在右子树（当右子树存在比给定键小的键时），不然就直接是根节点的键。向上取整（ceiling）类似，调换一下左右。

代码：

public Key floor(Key key) {
    Node x = floor(root, key);
    if (x == null) return null;
    return x.key;
}

private Node floor(Node x, Key key) {
    if (x == null) return null;
    int cmp = key.compareTo(x.key);

    if (cmp == 0) return x;
    if (cmp < 0) return floor(x.left, key);

    Node t = floor(x.right, key);
    if (t != null) return t;
    else return x;
}

图例：

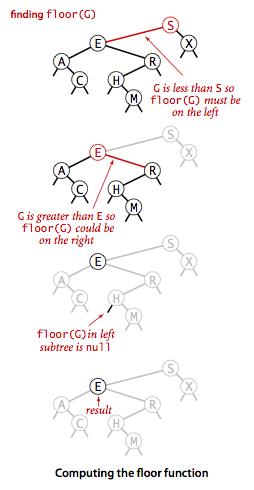
Rank

rank() 方法返回给定键的排名，为此我们在每个节点中维护一个变量 count，表示以该节点为根的树的节点数，并用方法 size() 访问。

private class Node {
    private Key key;
    private Value val;
    private Node left;
    private Node right;
    private int count;
}

public int size() {
    return size(root);
}

private int size(Node x) {
    if (x == null) return 0;
    return x.count;
}

private Node put(Node x, Key key, Value val) {
    if (x == null) return new Node(key, val, 1);
    int cmp = key.compareTo(x.key);
    if (cmp < 0) x.left = put(x.left, key, val);
    else if (cmp > 0) x.right = put(x.rigth, key, val);
    else x.val = val;
    x.count = 1 + size(x.left) + size(x.right);
    return x;
}

于是乎，方法 rank() 长这样：

public int rank(Key key) {
    return rank(key, root);
}

private int rank(Key key, Node x) {
    if (x == null) return 0;
    int cmp = key.compareTo(x.key);
    if (cmp < 0) return rank(key, x.left);
    else if (cmp > 0) return 1 + size(x.left) + rank(x.right);
    else return size(x.left);
}

二叉搜索树中这些顺序相关的操作，它们的复杂度同样和树高脱不了干系，这里只是举了些例子，完整的参见：BST.java。

deletion

最后来说说二叉查找树中的删除操作，有种懒删除是把节点标记成无效的而实际还在树里，也就是把值直接置空，但随着输入的增长，这做法显然不可取，空间上就不允许。

其实，在二叉树搜索树里删除没孩子的或只有一个孩子的节点，还是比较容易的，空出来的一条链接置空或者连到孩子上就好。像删除有最小键的节点就是这样：

代码：

public void deleteMin() {
    root = deleteMin(root);
}

private Node deleteMin(Node x) {
    if (x.left == null) return x.right;
    x.left = deleteMin(x.left);
    x.count = 1 + size(x.left) + size(x.right);
    return x;
}

代码先一直向左，直到找到一个左链接为空的节点，返回该节点的右链接，最后更新子树的节点数。

图例：

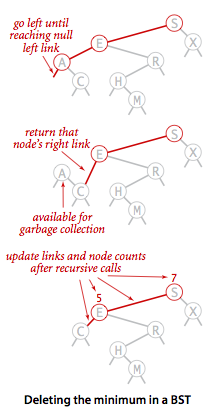
头大的是删除有两个孩子的节点，只空出来一条链接要怎么安排两个孩子，有个 Hibbard 删除的策略是用待删节点的后继节点（即右子树中键最小的节点）代替它，这样删除该点之后二叉查找树还是有序的。

具体做法可以概括成三步：

• 找到待删节点 t 的后继节点 x，x 是 t 右子树中具有最小键的节点，x 没有左孩子。
• 删掉 t 右子树中最小键的节点 x，不要让它被垃圾回收机制处理。
• 把节点 x 放在 t 的位置上。

图例：

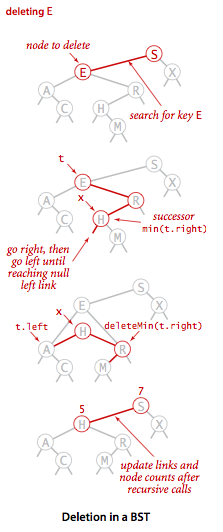
代码：

public void delete(Key key) {
    root = delete(root, key);
}

private Node delete(Node x, Key key) {
    if (x == null) return null;
    int cmp = key.compareTo(x.key);
    // search for key
    if (cmp < 0) x.left = delete(x.left, key);
    else if (cmp > 0) x.right = delete(x.right, key);
    else {
        if (x.right == null) return x.left;    // no right child
        if (x.left == null) return x.right;    // no left child
        // replace with successor
        Node t = x;
        x = min(t.right);
        x.right = deleteMin(t.right);
        x.left = t.left;
    }
    // update subtree counts
    x.count = size(x.left) + size(x.right) + 1;
    return x;
}

但是吧，Hibbard 删除里选后继节点是一个随意的决定，没有考虑树的对称性，为什么不选前继节点呢，实际上前继节点和后继节点的选择应该是随机的。一直是后继节点，可能会在某些实际应用中产生性能问题，大概就是树被删丑了的感觉。

维护一棵二叉查找树有”健康的“树高，或者说让二叉树平衡（左右子树差不多树也就低），是我们接下来要讨论的内容。