分形之列维(levy)曲线

莱维C形曲线（Lévy C curve）是个自我相似的分形，最先由保罗·皮埃尔·莱维在1938年的论文Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole描述和观察。levy曲线分形是将一条线段不停地分形成两条长度相等且相互垂直的线段,而生成的.

levy分形的最后很像一个英文字母C,其核心分形代码如下:

static void FractalC(const Vector3& vStart, const Vector3& vEnd, Vector3* pVertices)
{
    pVertices[] = vStart;
    pVertices[] = vEnd;

    pVertices[].x = (vStart.x + vStart.y + vEnd.x - vEnd.y) / ;
    pVertices[].y = (vEnd.x + vEnd.y + vStart.y - vStart.x) / ;
    pVertices[].z = 0.0f;

    pVertices[].x = pVertices[].x;
    pVertices[].y = pVertices[].y;
    pVertices[].z = 0.0f;
}

下面帖上levy的各级分形图:

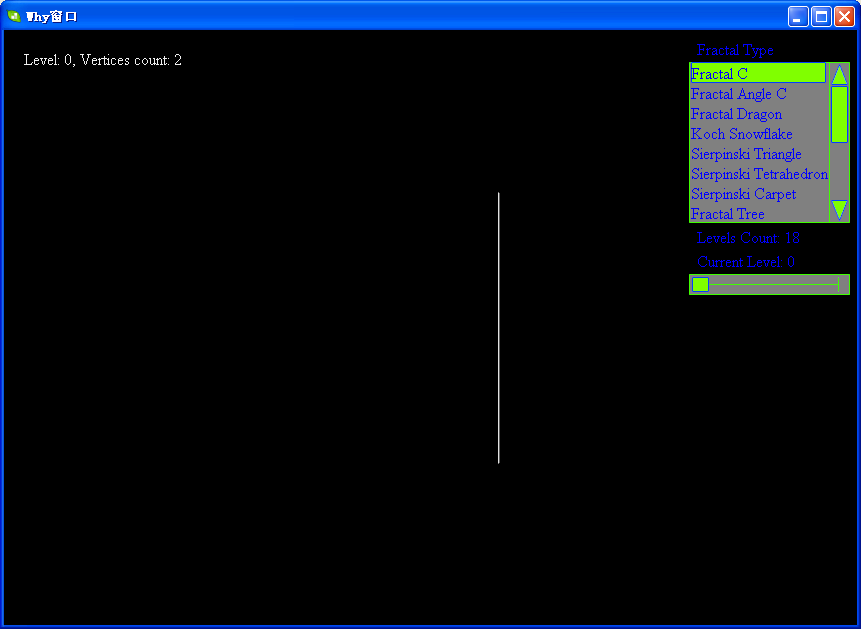
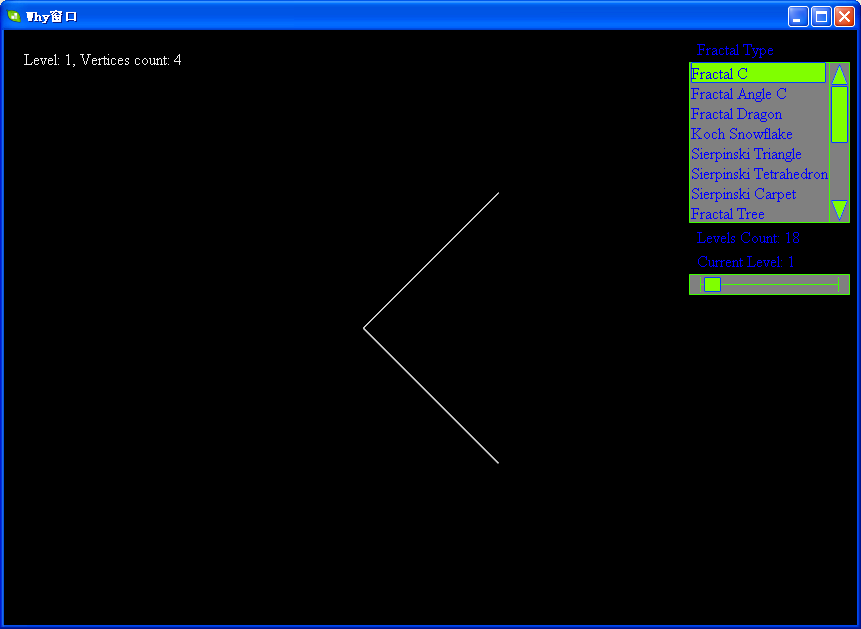
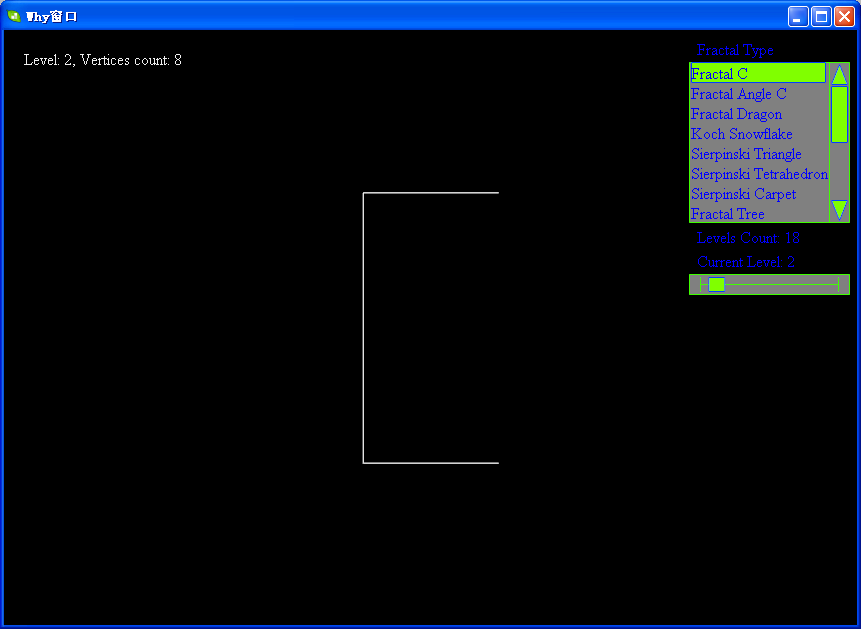
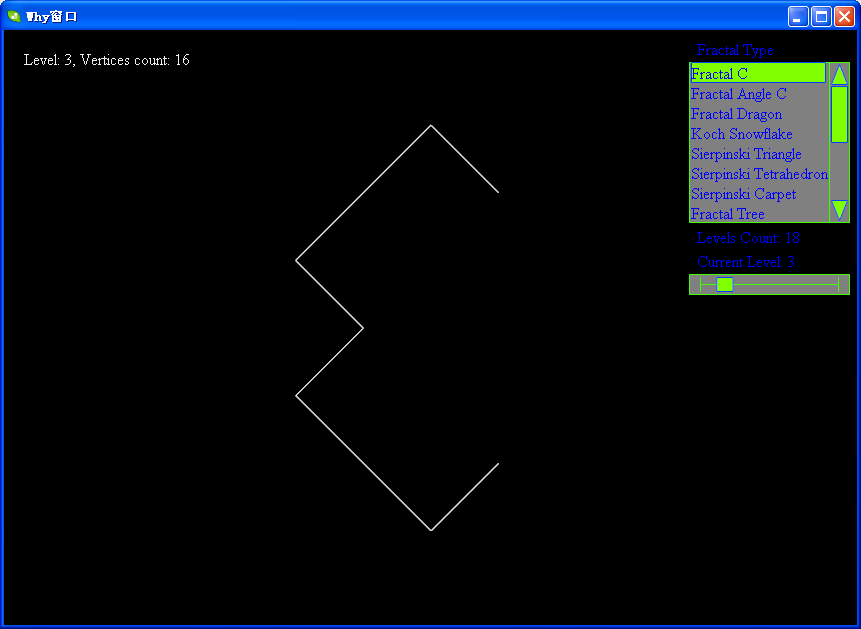
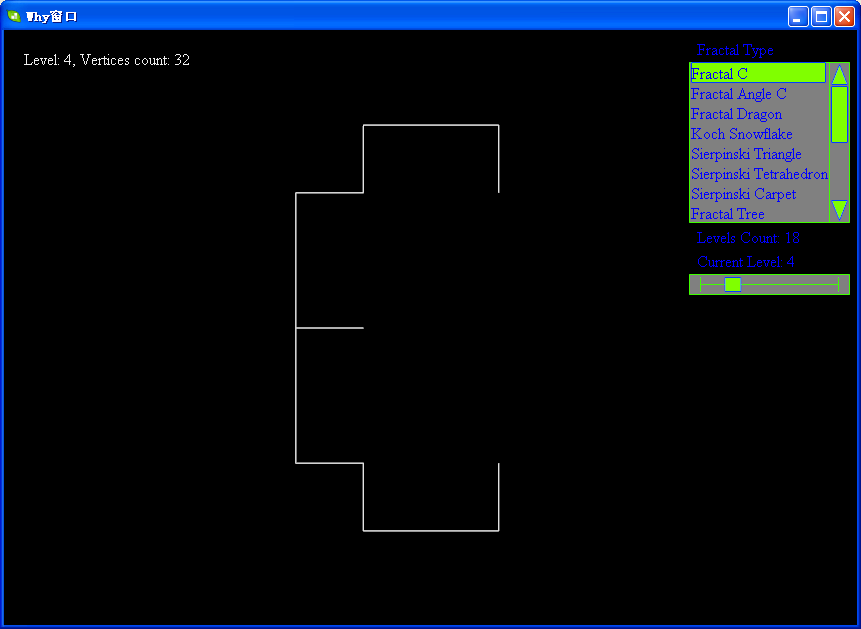
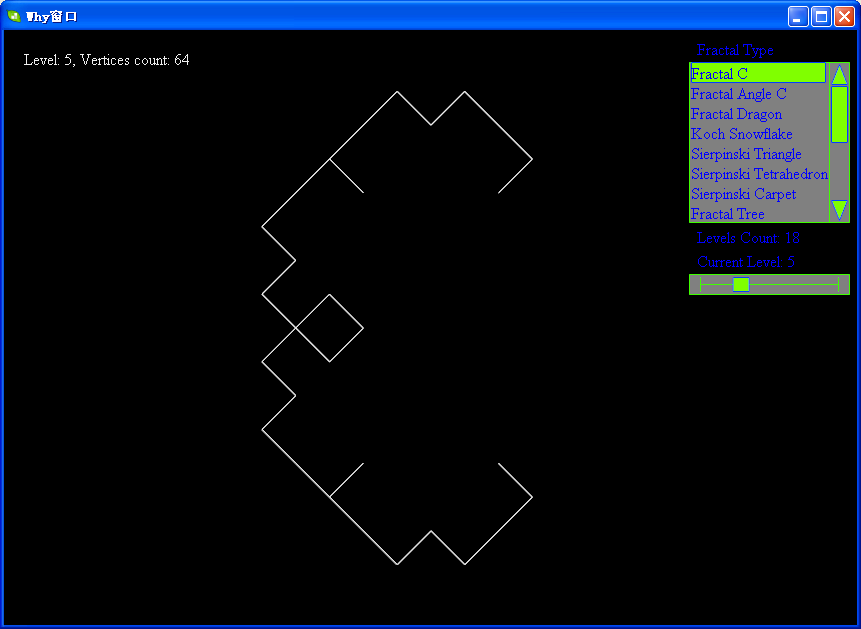
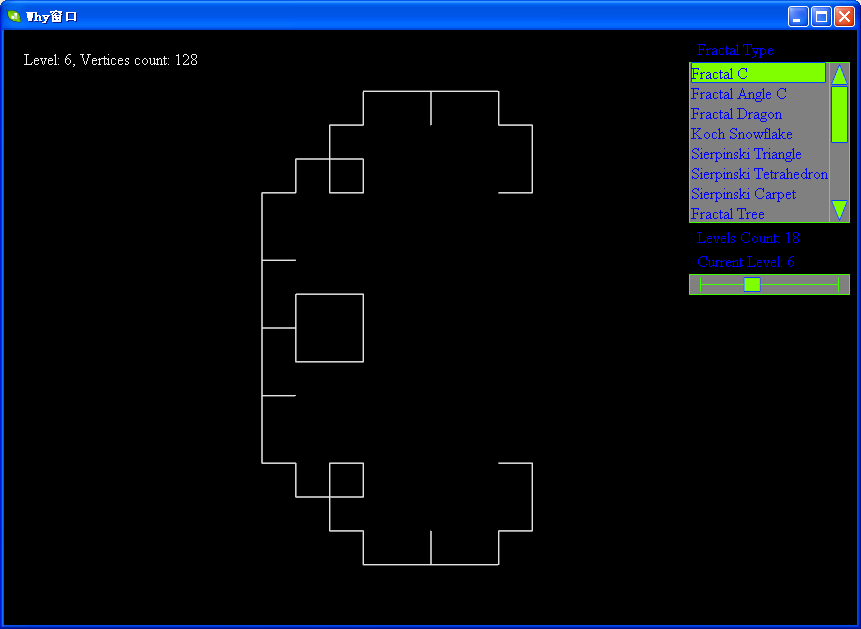
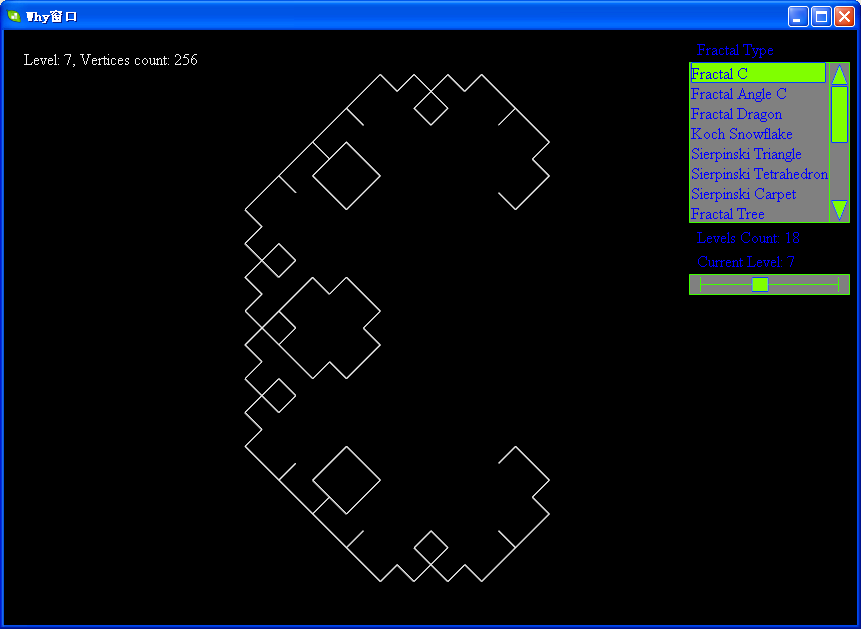
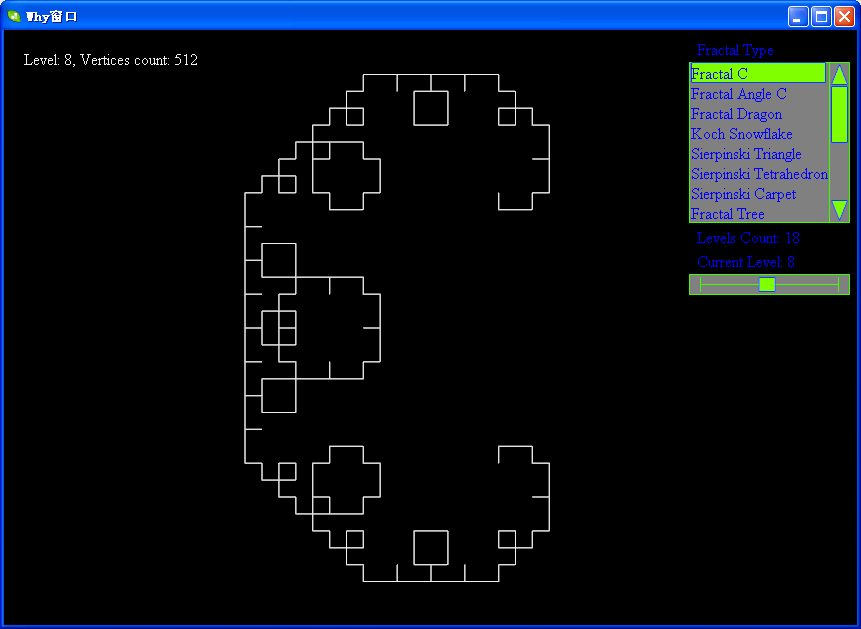
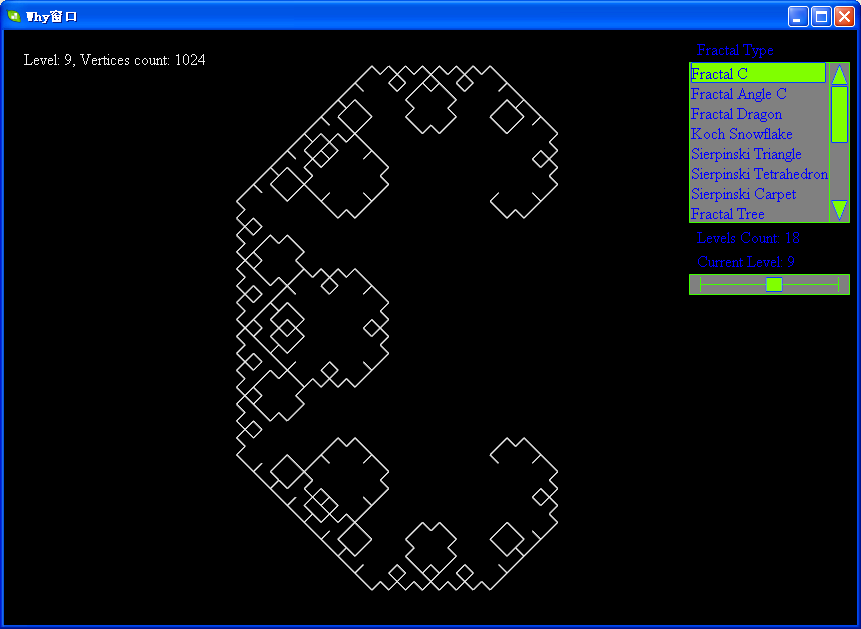
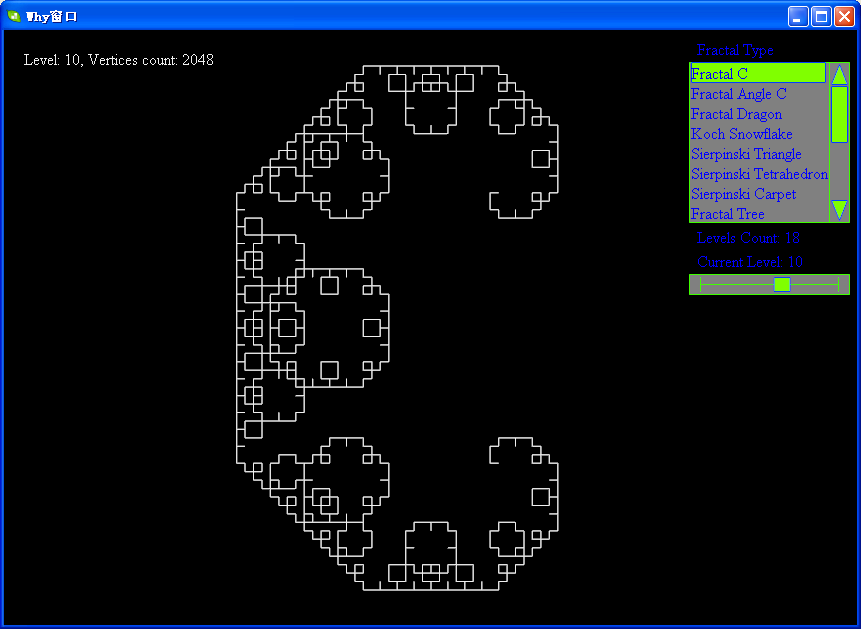
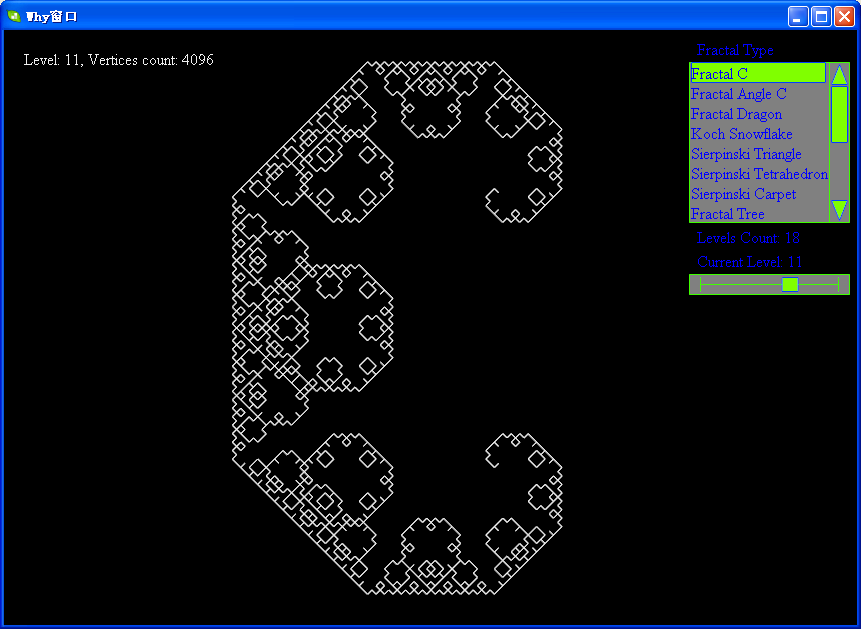
软件下载地址:http://files.cnblogs.com/WhyEngine/Fractal.7z