UVa1636 Headshot 【迁移自洛谷博客】

说明：小蒟蒻hkk现在正在做一些概率的题目，由于这方面和数学还有点关系，所以需要一些数学的思维，也需要表述出来，如夏军所述“把自己给讲懂”，所以写了些blog，主要为帮助自己理解。

题目大意

你和人决斗。决斗规则如下：用一把有n个弹槽的左轮手枪，对着自己脑袋来一枪，孰生孰死看天意。现在对方已经装了若干发子弹，并随机转了一下转轮，子弹呢用一个01序列表示，0表示这个弹槽无子弹，1表示有子弹。对方先对着自个脑袋开了一枪，嗯，你只听到了一声’click’，人还好好的，是空枪。现在轮到你了，摆在你面前的有两个选择，一是直接对自己开射，二是转一下转轮再来开射，显然你会选择生还希望更大的那种。

现在要做的就是根据子弹装填的序列，进行判断，如果直接shot生还希望大输出”SHOOT”，如果转一下生还希望大输出”ROTATE”，两种选择生还希望相同输出“EQUAL”.

##理解题意

一个手枪槽应该是这样的样子

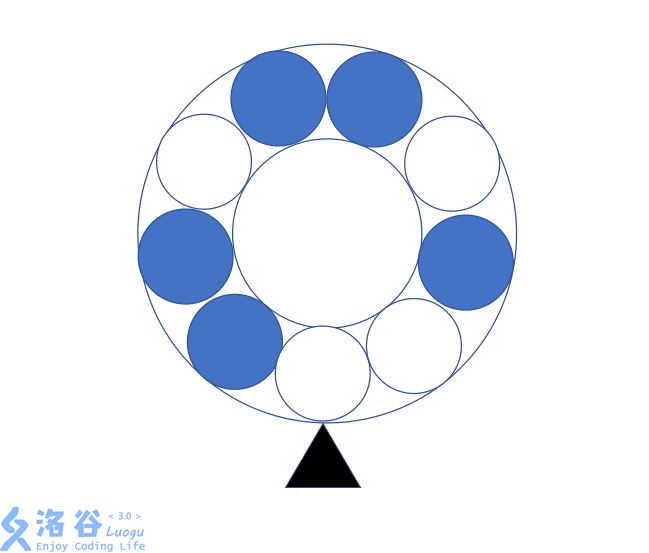
这样的一个手枪槽，现在，三角形指向的位置为即将发射的子弹的位置，在发射之前，可以转一下手枪槽，但是并不知道能转到什么位置。现在对方已经发射了一个空枪，然后槽转了一格，但是不知道那一个是否为空，现在要判断是转一下以后开枪还是直接开枪没有子弹的概率大。

##思路

假设我们没有转手枪，那么我们如果想要让下一刻子弹为空，说明我们必须是在连续的两个空弹上。所以我们假设有a个空弹，b个连续的空弹，n为总弹槽数，事件A为该弹为空，B为下一个子弹为空，则

\(P(B|A)=\frac{P(AB)}{P(B)}=\frac{\frac{b}{n}}{\frac{a}{n}}=\frac{b}{a}\)

还有一种情况为我们转了一下，那么，这个就比较简单了，对于发射空弹这个事件，有$$P(A)=\frac$$

那么，我们最终就只需要比较$P(B|A)$与$P(A)\(即可。也就是比较\)\frac\(与\)\frac$的大小。这里说一下，根据不等式的性质，由于a,b,n都是非负整数，所以我们把式子去一下分母，不等号方向也不用变，就变成比较$bn$与$a^2$的大小，就不需要进行浮点数运算了。

##代码

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;

const int maxn=100+7;
int n,cnt1,cnt2,cnt3;
int x,y;
char s[maxn];

void Init(){
    cnt1=cnt2=cnt3=0;
    scanf("%s",s+1);
    if(feof(stdin))exit(0);//读到文件末结束
    n=strlen(s+1);
    s[n+1]=s[1];//由于是环形，这样做比较方便
}

void Work(){
    for(register int i=1;i<=n;++i){
        if(s[i]=='0'&&s[i+1]=='0')++cnt1,++cnt2;
        else if(s[i]=='0'&&s[i+1]=='1')++cnt2;
        if(s[i]=='0')++cnt3;
    }
//    cnt1:连续2个0的个数，cnt2:0的个数，cnt3和cnt2等价，cnt3是我一时发疯开的
    x=cnt1*n;y=cnt3*cnt2;//交叉相乘
    if(x==y)printf("EQUAL\n");
    else if(x<y)printf("ROTATE\n");
    else printf("SHOOT\n");
}

int main(){
    while(!feof(stdin)){
        Init();
        Work();
    }
    return 0;
}

——发布时间：2017-12-13 13:25:13