【纪中集训】2019.08.10【省选组】模拟TJ

前言

• 一套码农题……

T1

Description

• 给定一棵\(n(\in[2,10^5])\)个点的树，\(m(≤10^5)\)次询问，每次询问有两个不相同的点，要让所有点走到这两个点之一（走一条边耗费1单位时间，所有点同时出发），求最少耗时。

SolutionⅠ

• 这题有一个简单又自然的方法：LCT！
• 我们用LCT求出询问点的中间两点，断开其中的边；然后分别把两个询问点makeroot，查询各自的树的深度最大值。
• 注意虚边的所带出的深度最大值也要算上；而维护这东西还要打个set/multiset。而且由于LCT有翻转操作，我们要求一个正着的深度最大值和反着的最大值，翻转的时候直接交换它们即可。

SolutionⅡ

• 这题是不是有那么一点像……noip2018D3T3？
• 没错！我们可以倍增！设两个倍增数组\(up[i][j]\)、\(dw[i][j]\)分别表示\(i\)到它的第\(2^j\)个祖先的链上所有点的儿子的子树（不把\(i\)的子树计算在内，后文对于这种类似的简记为\(a\)到\(b\)）走到它的\(2^j\)个祖先/走到\(i\)的答案。
• 对于一个询问\((x,y)\)（不妨钦定\(deep_x≥deep_y\)），我们找到\(z=lca(x,y)\)，并找到\((x,y)\)的中间点\(z1\)。那么答案的计算就分为六个部分：1.\(x\)的子树全部走到\(x\)；2.\(x\)到\(z1\)全部走到\(x\)；3.\(z1\)到\(z\)全部走到\(y\)；4.\(y\)到\(z\)全部走到\(y\)；5.\(y\)的子树全部走到\(y\)；6.\(z\)的子树以外所有点以及\(z\)的儿子（不含\(x\)、\(y\)的祖先）的子树全部走到\(y\)。

Code

• 这倍增，比LCT还难打……

#include <cstdio>
#include <vector>
#include <algorithm>
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
typedef long long ll;

const int N=11e4;
int n,x,y,z,f[N][17],dep[N],in[N],out[N],dw[N][17],up[N][17],m,todep,z1,z2,ans;
vector<int> e[N];

void MAX(int&x,int y) {if(x<y) x=y;}
int max(int x,int y) {return x>y?x:y;}

void dfs(int x)
{
	vector<int>::iterator it; int y;
	for(it=e[x].begin(); it!=e[x].end(); it++)
		if((y=*it)^f[x][0])
		{
			f[y][0]=x, dep[y]=dep[x]+1, dfs(y);
			MAX(dw[y][0],in[x]+1);
			MAX(up[y][0],in[x]);
			MAX(in[x],in[y]+1);
		}
	int g=0;
	for(it--; 233; it--)
	{
		if((y=*it)^f[x][0])
		{
			MAX(dw[y][0],g+1);
			MAX(up[y][0],g);
			MAX(g,in[y]+1);
		}
		if(it==e[x].begin()) break;
	}
}

int lca(int x,int y)
{
	fd(i,16,0) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
	if(x==y) return x;
	fd(i,16,0) if(f[x][i]^f[y][i]) x=f[x][i],y=f[y][i];
	return f[x][0];
}

int main()
{
	scanf("%d",&n);
	fo(i,1,n-1)
	{
		scanf("%d%d",&x,&y);
		e[x].push_back(y);
		e[y].push_back(x);
	}
	dfs(dep[1]=1);
	fo(i,1,16)
		fo(x,1,n)
		{
			if(!(f[x][i]=f[y=f[x][i-1]][i-1])) continue;
			dw[x][i]=max(dw[x][i-1],dw[y][i-1]+(1<<i-1));
			up[x][i]=max(up[x][i-1]+(1<<i-1),up[y][i-1]);
		}
	fo(x,1,n)
	{
		z1=x;
		fd(i,16,0)
			if(f[z1][i])
			{
				MAX(out[x],dw[z1][i]+dep[x]-dep[z1]);
				z1=f[z1][i];
			}
	}
	for(scanf("%d",&m); m--;)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		if(dep[x]<dep[y]) swap(x,y);
		z=lca(x,y);
		todep=(z^y?dep[x]-(dep[x]+dep[y]-2*dep[z]-1>>1):(dep[x]+dep[y]>>1)+1);
		z1=x, ans=max(in[x],out[z]+dep[y]-dep[z]);
		fd(i,16,0)
			if(dep[f[z1][i]]>=todep)
			{
				MAX(ans,dw[z1][i]+dep[x]-dep[z1]);
				z1=f[z1][i];
			}
		fd(i,16,0)
			if(dep[f[z1][i]]>dep[z])
			{
				MAX(ans,up[z1][i]+dep[f[z1][i]]+dep[y]-2*dep[z]);
				z1=f[z1][i];
			}
		x=z1;
		if(z^y)
		{
			MAX(ans,in[z1=y]);
			fd(i,16,0)
				if(dep[f[z1][i]]>dep[z])
				{
					MAX(ans,dw[z1][i]+dep[y]-dep[z1]);
					z1=f[z1][i];
				}
			for(vector<int>::iterator it=e[z].begin(); it!=e[z].end(); it++)
				if((z2=*it)^f[z][0]&&z2^x&&z2^z1)
					MAX(ans,in[z2]+1+dep[y]-dep[z]);
		}
		else	MAX(ans,up[z1][0]);
		printf("%d\n",ans);
	}
}

T2

Description

• 给出一棵以1号点为根的\(n(\in[2,10^5])\)个点的树，并会给出每个点的儿子排列（要按照它的顺序求dfn序）。有\(m\)个操作，操作有三种：
• 操作Ⅰ：询问两个点的距离；
• 操作Ⅱ：给出v和h，断开v和他父亲的边，然后将它和它第h个祖先相连；
• 操作Ⅲ：求深度为\(k\)的点中dfn序最大的点。

SolutionⅠ

• 此法由cc dalao提供。
• 用LCT维护树的形态以及操作Ⅰ；再开一棵splay维护原树的dfn序。由于我们可以用LCT维护子树大小，所以很方便知道要搬多少点，操作Ⅱ迎刃而解；操作Ⅲ的话，可以在splay上二分，尽量走右儿子即可。

SolutionⅡ

• ETT（欧拉游览树，用splay维护括号序）。
• 我们把原树的每个点拆成两个括号，左括号值为1，右括号值为-1；这样有一个很好的性质：原树中一个点的深度就等于它所对应的左括号的前缀和。这样的话，我们记录下原树中每个点对应的括号标号；而splay中每个点记录它的值、子树和、子树中最大/最小前缀和。
• 操作Ⅰ的话，可以找到那两个点所对应的左括号，那它们的lca的深度肯定是两个左括号之间最小的前缀和。
• 操作Ⅱ就直接把v的子树拎出来，查询第h个祖先就相当于查询dfn序在v之前、深度（前缀和）恰好为\(deep_v-h\)的最后一个点。这个可以在splay上二分，也是尽量走右儿子。
• 操作Ⅲ就二分出全树中深度为\(k\)的最后一个点。

Code

• 下面的代码中，在splay上二分后我并没有做伸展操作。这样做并非均摊\(O((n+m)\log_2n)\)，而是最坏\(O(nm)\)。不过考虑到出题人懒，数据大部分随机，二分后伸展反而跑得更慢。

#include <cstdio>
#define A son[x][0]
#define B son[x][1]
#define A1 son[y][0]
#define B1 son[y][1]
#define fo(i,a,b) for(int i=a;i<=b;i++)
using namespace std;

const int N=21e4;
int n,m,l,a[N],pa[N],to[N],ne[N],la[N],ti,p[N],v[N],fa[N],son[N][2],s[N],mx[N],mn[N],rt;

void ins(int x,int y) {static int tot=0; pa[to[++tot]=y]=x, ne[tot]=la[x], la[x]=tot;}

void dfs(int x)
{
	v[p[++ti]=(x<<1)-1]=1;
	for(int i=la[x],y; y=to[i]; i=ne[i]) dfs(y);
	v[p[++ti]=x<<1]=-1;
}

int max(const int&x,const int&y) {return x>y?x:y;}
int min(const int&x,const int&y) {return x<y?x:y;}
bool so(int x) {return son[fa[x]][1]==x;}
void link(int y,int x,bool k)
{
	if(y) son[y][k]=x;
	if(x) fa[x]=y;
}
void up(int x)
{
	s[x]=s[A]+v[x]+s[B];
	mx[x]=max(mx[A],s[A]+v[x]+max(mx[B],0));
	mn[x]=min(mn[A],s[A]+v[x]+min(mn[B],0));
}
int build(int l,int r)
{
	int mid=l+r>>1,&x=p[mid];
	if(l<mid) link(x,build(l,mid-1),0);
	if(mid<r) link(x,build(mid+1,r),1);
	up(x);
	return x;
}
void rot(int x)
{
	if(!x) return;
	int y=fa[x],z=fa[y],k=so(x),b=son[x][!k];
	link(y,b,k);
	link(z,x,so(y));
	link(x,y,!k);
	up(y), up(x);
}
void splay(int x,int y) {for(int f=fa[x]; f^y; rot(x),f=fa[x]) rot(fa[f]^y?so(x)==so(f)?f:x:0);}
int MIN(int&x,const int&y) {if(x>y) x=y;}
int dis(int x,int y)
{
	x=(x<<1)-1, y=(y<<1)-1;
	int dx,dy,dl;
	splay(x,0), dx=s[A]+v[x];
	splay(y,0), dy=s[A1]+v[y];
	splay(x,y), rt=y;
	dl=min(dx,dy);
	MIN(dl, A1==x ? s[A]+v[x]+mn[B] : s[A1]+v[y]+mn[A] );
	return dx+dy-2*dl;
}
int find(int x,int k)
{
	while(233)
	{
		int k1=k-s[A]-v[x];
		if(mn[B]<=k1&&k1<=mx[B]) {k=k1,x=B; continue;}
		if(s[A]+v[x]==k) return x&1?x+1>>1:pa[x>>1];
		x=A;
	}
}
int pre(int x) {splay(x,0); for(x=A;B;x=B); return x;}
int nxt(int x) {splay(x,0); for(x=B;A;x=A); return x;}
void move(int u,int h)
{
	int x=(u<<1)-1,L,R,t;
	splay(x,0);
	pa[u]=find(A,s[A]+v[x]-h);
	L=pre(x), R=nxt(x+1);
	splay(L,0), splay(R,L);
	t=son[R][0], son[R][0]=0;
	up(R), up(L);
	L=pre(R=pa[u]<<1);
	splay(L,0), splay(R,L);
	link(R,t,0);
	up(R), up(rt=L);
}

int main()
{
	scanf("%d%d",&n,&m);
	fo(i,1,n)
	{
		scanf("%d",&l);
		fo(j,1,l) scanf("%d",&a[j]), pa[a[j]]=i;
		while(l) ins(i,a[l--]);
	}
	dfs(1);
	mn[0]=N, mx[0]=-N;
	rt=build(1,ti);
	int tp,x,y;
	while(m--)
	{
		scanf("%d%d",&tp,&x);
		switch(tp)
		{
			case 1:scanf("%d",&y);
			printf("%d\n",x^y?dis(x,y):0);
			break;

			case 2:scanf("%d",&y);
			move(x,y);
			break;

			case 3:printf("%d\n",find(rt,x+1));
			break;
		}
	}
}

T3

Description

• 描述实在太复杂了，上图。
  
  
• 对于30% 的数据，n,m <= 5，数据组数<=7
• 对于100% 的数据，2 <= n,m <= 50，数据组数<= 17

Solution

• DP！
• 可以预处理只有左上、右上、左下、右下、上下方向的象鼻时最多引用的水量。然后可以分为下图所示的三种情况：
  
  
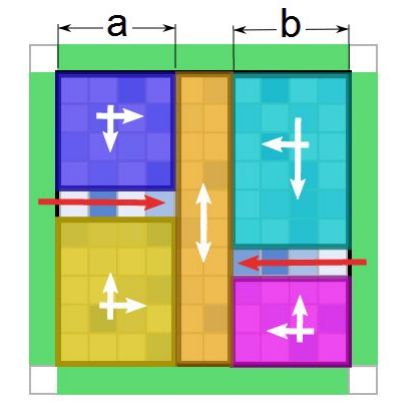
• 当然这还有一种左右向的，由上图旋转90°可得。为了简便，我是将原图的行、列交换。
  
  
  
  
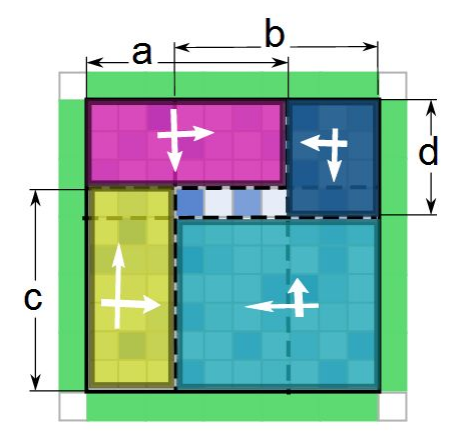
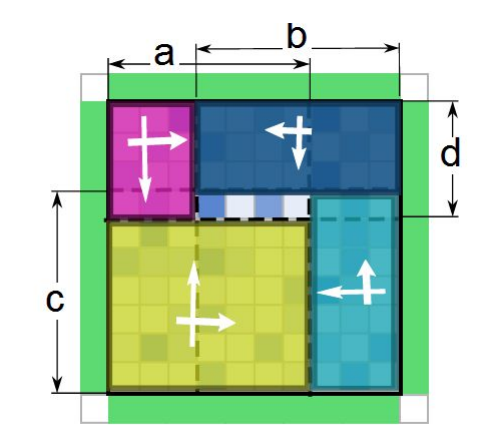
• 可以发现第三张图左右（或者上下）翻转就得到第二张图。

Code

#include <cstdio>
#include <cstring>
#include <algorithm>
#define max(x,y) (x>y?x:y)
#define C(a) memset(a,0,sizeof a);
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
using namespace std;

const int N=55;
int n,a[N][N],u[N][N],l[N][N],d[N][N],r[N][N];
int ul[N][N],ur[N][N],dl[N][N],dr[N][N],ud[N][N],ans;
char s[N][N];

inline void MAX(int&x,const int&y) {if(x<y)x=y;}

void init(bool k)
{
	fo(i,1,n)
	{
		fo(j,1,n)
		{
			u[i][j]=max(u[i-1][j],a[i][j]);
			l[i][j]=max(l[i][j-1],a[i][j]);
			ul[i][j]=max(ul[i][j-1]+u[i][j],ul[i-1][j]+l[i][j]);
		}
		fd(j,n,1)
		{
			r[i][j]=max(r[i][j+1],a[i][j]);
			ur[i][j]=max(ur[i][j+1]+u[i][j],ur[i-1][j]+r[i][j]);
		}
	}
	fd(i,n,1)
	{
		fo(j,1,n)
		{
			d[i][j]=max(d[i+1][j],a[i][j]);
			dl[i][j]=max(dl[i][j-1]+d[i][j],dl[i+1][j]+l[i][j]);
		}
		fd(j,n,1) dr[i][j]=max(dr[i][j+1]+d[i][j],dr[i+1][j]+r[i][j]);
	}
	if(k) return;
	fo(j,1,n)
	{
		ud[j][j]=0;
		fo(i,0,n) MAX(ud[j][j],u[i][j]+d[i+1][j]);
	}
	fo(i,1,n-1) fo(j,i+1,n) ud[i][j]=ud[i][j-1]+ud[j][j];
}

void calc1()
{
	fo(i,0,n)
		fo(j,0,n)
			fo(k,0,n)
				fo(l,k+1,n+1)
					MAX(ans,ul[i][k]+ur[j][l]+ud[k+1][l-1]+dl[i+1][k]+dr[j+1][l]);
}

void calc2()
{
	fo(i,0,n)
		fo(j,1,i)
			fo(k,0,n)
				fo(l,1,k)
					MAX(ans,ul[i][l-1]+ur[j-1][l]+dl[i+1][k]+dr[j][k+1]);
}

int main()
{
	while(~scanf("%d",&n))
	{
		C(u) C(l) C(d) C(r)
		C(ul) C(ur) C(dl) C(dr) C(ud)
		fo(i,1,n)
		{
			scanf("%s",s[i]+1);
			fo(j,1,n) a[i][j]=s[i][j]^48;
		}

		ans=0;
		init(0), calc1();

		fo(i,1,n-1) fo(j,i+1,n) swap(a[i][j],a[j][i]);
		init(0), calc1();

		calc2();

		fo(i,1,n) fo(j,1,n/2) swap(a[i][j],a[i][n-j+1]);
		init(1), calc2();

		printf("%d\n",ans);
	}
}