NOIP2015 提高组 Day T3 斗地主

题目描述

牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共5张牌来进行的扑克牌游戏。在斗地主中，牌的大小关 系根据牌的数码表示如下：3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王，而花色并不对牌的大小产生影响。每一局游戏中，一副手牌由 n 张牌组成。游戏者每次可以根据规定的牌型进行出牌，首先打光自己的手牌一方取得游戏的胜利。

现在，牛牛只想知道，对于自己的若干组手牌，分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。

需要注意的是，本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。具体规则如下：

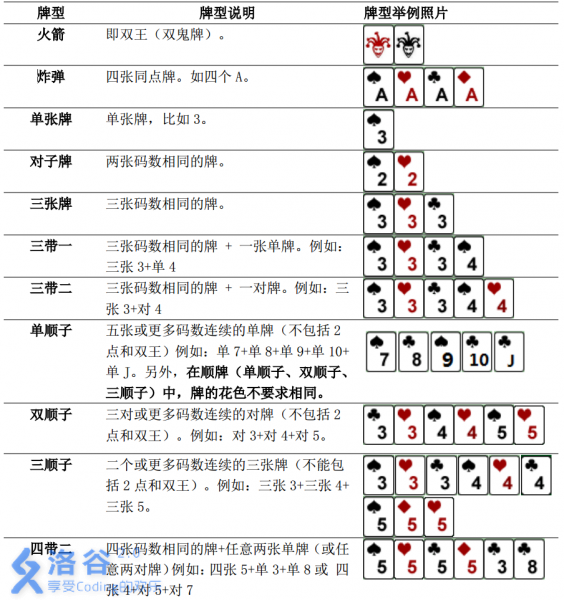
输入输出格式

输入格式

第一行包含用空格隔开的2个正整数 T,n ，表示手牌的组数以及每组手牌的张数。

接下来 T 组数据，每组数据 n 行，每行一个非负整数对 $ a_i , b_i $ ，表示一张牌，其中 $ a_i \(表示牌的数码，\) b_i $ 表示牌的花色，中间用空格隔开。特别的，我们用 1 来表示数码 A， 11 表示数码J ， 121212 表示数码Q，13表示数码 K；黑桃、红心、梅花、方片分别用 1−4 来表示；小王的表示方法为 01 ，大王的表示方法为 02 。

输出格式

共 T 行，每行一个整数，表示打光第 iii 组手牌的最少次数。

输入输出样例

输入样例#1

1 8

7 4

8 4

9 1

10 4

11 1

5 1

1 4

1 1

输出样例#1

3

输入样例#2

1 17

12 3

4 3

2 3

5 4

10 2

3 3

12 2

0 1

1 3

10 1

6 2

12 1

11 3

5 2

12 4

2 2

7 2

输出样例#2

6

样例解释

样例1说明

共有1组手牌，包含8张牌：方片7，方片8，黑桃9，方片10，黑桃J，黑桃5，方片A以及黑桃A。可以通过打单顺子（方片7，方片8，黑桃9，方片10，黑桃J），单张牌（黑桃5）以及对子牌（黑桃A以及方片A）在3次内打光。

对于不同的测试点， 我们约定手牌组数T与张数n的规模如下：

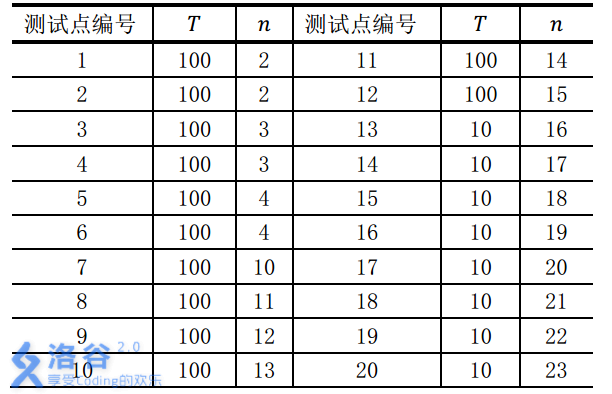
解析

该做法有一个前提，数据是随机的，出牌顺序对后来的决策没有影响。

似乎是一道搜索+贪心+模拟的题目。在所有出牌规则中，我们先寻找形式固定的四带二、三带一、炸弹、三张牌、对子（火箭也算对子）和单张牌。设b[i]表示张数为i的牌有多少种。对于四带二，如果有四张的，我们就依次看b[2]是否大于等于2、b[1]是否大于等于1、b[2]是否大于等于1,。满足条件就按对应情况出牌。三带一同理。每出一次就把带的牌在b中对应的种数减掉。那么最后剩下的b中的值的和就是我们如果要出完手中的牌不计顺子所需要次数。用它去更新答案。注意，这个是有用的，在只能单个组合打出时它能统计答案。然后是顺子。其实每个顺子都差不多，用两重循环在计数数组a中找到满足条件的连续的牌并减去对应的值，如果不连续了就退出。如果连续区间的长度大于要求长度就搜索下一层。记得退出时复原a数组。注意K和A也算是连续的。

代码

#include <iostream>
#include <cstdio>
#include <cstring>
#define N 15
using namespace std;
int t,n,i,a[N],ans,len[4]={0,5,3,2};
void dfs(int);
void shunzi(int t,int x)
{
	for(int i=1;i<=12;i++){
		int k=12;
		for(int j=i;j<=12;j++){
			a[j]-=t;
			if(a[j]<0){
				k=j;
				break;
			}
			if(j-i+1>=len[t]) dfs(x+1);
		}
		for(int j=k;j>=i;j--) a[j]+=t;
	}
}
void dfs(int x)
{
	int b[5]={0};
	for(int i=0;i<=13;i++) b[a[i]]++;
	for(int i=1;i<=13;i++){
		if(a[i]==4){
		    if(b[2]>=2) b[2]-=2;
			else if(b[1]>=2) b[1]-=2;
			else if(b[2]>=1) b[2]--;
		}
	}
	for(int i=1;i<=13;i++){
		if(a[i]==3){
			if(b[1]>=1) b[1]--;
			else if(b[2]>=1) b[2]--;
		}
	}
	ans=min(ans,x+b[1]+b[2]+b[3]+b[4]);
	for(int i=1;i<=3;i++) shunzi(i,x);
}
int main()
{
	cin>>t>>n;
	while(t--){
		memset(a,0,sizeof(a));
	    ans=1<<30;
		for(i=1;i<=n;i++){
			int x,col;
			cin>>x>>col;
			if(x==0) a[x]++;
			else if(x<=2) a[x+11]++;
			else a[x-2]++;
		}
		dfs(0);
		cout<<ans<<endl;
	}
	return 0;
}