吴恩达机器学习101:SVM优化目标
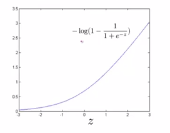
1.为了描述SVM,需要从logistic回归开始进行学习,通过改变一些小的动作来进行支持向量机操作。在logistic回归中我们熟悉了这个假设函数以及右边的sigmoid函数,下式中z表示θ的转置乘以x,
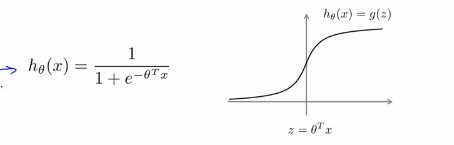
(1)如果我们有一个样本,其中y=1,这样的一个样本来自训练集或者测试集或者交叉验证集,我们希望h(x)能尽可能的接近1。因此我们想要正确的将样本进行分类,如果h(x)趋近于1,就意味着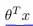 远大于0,即
远大于0,即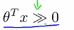 。
。
(2)相应的如果y=0,我们想hθ(x)=0,那么 远远小于0,即
远远小于0,即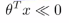
(3)logistic regresssion的代价函数:
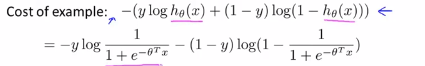
如果y=1,当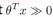 的时候,我们可以画下图:
的时候,我们可以画下图:
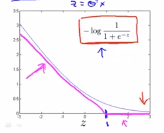
如果y=0,当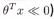 ,我们可以画下图:
,我们可以画下图:
线性回归代价函数:
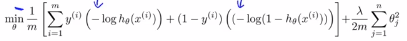
支持向量机代价函数:
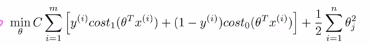
与logistic回归不同的是,支持向量机并不会输出概率,而是优化上面的这个代价函数,得到一个参数θ,而支持向量机所做的是进行了一个直接的预测,预测y是0还是1.所以如果θ的转置乘以x的值大于0,那么它就会输出1;如果θ的转置乘以x的转置小于0 ,那么它就会输出0
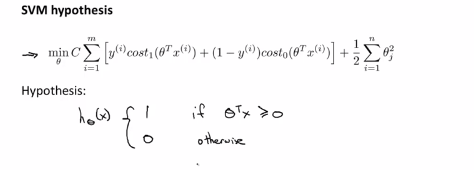
吴恩达机器学习101:SVM优化目标的更多相关文章
- 吴恩达机器学习笔记48-降维目标:数据压缩与可视化(Motivation of Dimensionality Reduction : Data Compression & Visualization)
目标一:数据压缩 除了聚类,还有第二种类型的无监督学习问题称为降维.有几个不同的的原因使你可能想要做降维.一是数据压缩,数据压缩不仅允许我们压缩数据,因而使用较少的计算机内存或磁盘空间,而且它也让我们 ...
- ML:吴恩达 机器学习 课程笔记(Week1~2)
吴恩达(Andrew Ng)机器学习课程:课程主页 由于博客编辑器有些不顺手,所有的课程笔记将全部以手写照片形式上传.有机会将在之后上传课程中各个ML算法实现的Octave版本. Linear Reg ...
- 吴恩达机器学习笔记47-K均值算法的优化目标、随机初始化与聚类数量的选择(Optimization Objective & Random Initialization & Choosing the Number of Clusters of K-Means Algorithm)
一.K均值算法的优化目标 K-均值最小化问题,是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和,因此 K-均值的代价函数(又称畸变函数 Distortion function)为: 其中
- [吴恩达机器学习笔记]12支持向量机3SVM大间距分类的数学解释
12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.3 大间距分类背后的数学原理- Mathematic ...
- 吴恩达机器学习笔记58-协同过滤算法(Collaborative Filtering Algorithm)
在之前的基于内容的推荐系统中,对于每一部电影,我们都掌握了可用的特征,使用这些特征训练出了每一个用户的参数.相反地,如果我们拥有用户的参数,我们可以学习得出电影的特征. 但是如果我们既没有用户的参数, ...
- [吴恩达机器学习笔记]13聚类K-means
13.聚类 觉得有用的话,欢迎一起讨论相互学习~Follow Me 13.1无监督学习简介 从监督学习到无监督学习 在一个典型的监督学习中,我们有一个有标签的训练集,我们的目标是找到能够区分正样本和负 ...
- 吴恩达机器学习笔记41-支持向量机的优化目标(Optimization Objective of Support Vector Machines)
- 吴恩达机器学习笔记45-使用支持向量机(Using A SVM)
本篇我们讨论如何运行或者运用SVM. 在高斯核函数之外我们还有其他一些选择,如:多项式核函数(Polynomial Kernel)字符串核函数(String kernel)卡方核函数( chi-squ ...
- [吴恩达机器学习笔记]12支持向量机2 SVM的正则化参数和决策间距
12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.2 大间距的直观理解- Large Margin I ...
随机推荐
- CentOS 7,使用yum安装Nginx
https://www.centos.bz/2018/01/centos-7%EF%BC%8C%E4%BD%BF%E7%94%A8yum%E5%AE%89%E8%A3%85nginx/ 文章目录 [隐 ...
- LeetCode 34. 搜索范围(search for a range)
题目描述 给定一个按照升序排列的整数数组 nums,和一个目标值 target.找出给定目标值在数组中的开始位置和结束位置. 你的算法时间复杂度必须是 O(log n) 级别. 如果数组中不存在目标值 ...
- 第四章 SpringCloud之Eureka-Client实现服务(Jpa,H2)
1.pom.xml <?xml version="1.0" encoding="UTF-8"?> <project xmlns="h ...
- Java学习之==>IO文件操作体系
一.概述 在整个 Java.io 中最重要的就是5个类和一个接口.5个类指的是 File.InputStream.OutputStream.Reader.Writer,一个接口指的是Serializa ...
- linux判断httpd端口是否打开
判断端口是否打开 lsof -i:80 判断端口打开了几个 lsof -i:80 | wc -l
- SI_WorkShop_V4安装手册
V4安装手册 第一步 启动workshopV4 解压workshopV4.rar,在解压后的目录中双击eclipse.exe启动workshopV4,启动画面如下图所示:(注:解压后第1次启动速度会慢 ...
- java:常用类(包装类,equals和==的比较,Date,java.lang.String中常用方法,枚举enum)
*包装类: 将基本类型封装成类,其中包含属性和方法以方便对象操作. *byte---->Byte *short--->Short *long--->Long *float---> ...
- LeetCode.961-2N数组中N次重复的元素(N-Repeated Element in Size 2N Array)
这是悦乐书的第365次更新,第393篇原创 01 看题和准备 今天介绍的是LeetCode算法题中Easy级别的第227题(顺位题号是961).在大小为2N的数组A中,存在N+1个唯一元素,并且这些元 ...
- P1551 亲戚
这里是题面啊~ 这道题我就不多说了,基本(好吧没有基本)就是一道模板题,读入+并查集+输出,完美结束 #include<set> #include<map> #include& ...
- DN值
DN值(Digital Number )是遥感影像像元亮度值,记录的地物的灰度值.无单位,是一个整数值,值大小与传感器的辐射分辨率.地物发射率.大气透过率和散射率等有关. 从DN值计算大气顶的反射率使 ...
