基于Diff机制的多个状态合并

1. 场景

假设一个系统System在某一时刻的状态可以用State A来表示【State里面包含着一些元素的集合】:

   1: State A = [element_0, element_1,……,element_n]

系统System经过了一段时间的运行，在另一时刻，它的状态变成State B:

   1: State B = [element_0, element_1,……,element_n]

在系统System运行时，会实时生成其中元素变化的日志，日志的内容包含了某个元素的“Add, Delete, Modify”记录。

那么系统System从State A变化到State B，会积累一组变化的日志Diff 1，其中记录了许多条各个元素的变化历史，某一个元素element_n可能会对应到多条的变化记录，比如

   1: [Add, Modify, Delete, Add, Modify, Modify,……]

2. 归纳Diff记录

因此，需要把Diff 1做一个归纳操作，从而得到一个三元组Delta 1，每一项是一个集合，分别保存着“Add”，“Delete”，“Modify”的元素的集合：

   1: Delta 1 = ([Added element 1, Added element 2, ......, Added element n], [Deleted element 1, Deleted element 2, ......, Deleted element n], [Modified element 1, Modified element 2, ......, Modified element n])

分析Diff的记录可以知道，对于一个特定的element，只要知道其在Diff中的第一条记录和最后一条记录，就可以得到它在Diff这段时间内的变化类型

No.	First Diff Record Type	Last Diff Record Type	Summary Change Type
1	Add	Add	Add
2	Add	Delete	Temporary
3	Add	Modify	Add
4	Delete	Add	Modify
5	Delete	Delete	Delete
6	Delete	Modify	Modify
7	Modify	Add	Modify
8	Modify	Delete	Delete
9	Modify	Modify	Modify

3. 多个Diff的归纳三元组的合并

如果我们知道了系统System从State A到State B的Diff归纳后得到的三元组Delta 1，以及系统System从State B到时State C的三元组Delta 2，那么我们怎么能够得到从State A到State C的三元组Delta 3呢？

我们假设

   1: Delta 1 = (Added Set A1, Deleted Set D1, Modified Set M1)

   2: Delta 2 = (Added Set A2, Deleted Set D2, Modified Set M2)

将对应的集合Set进行Union操作

   1: Set A3 = A1 Union A2

   2: Set D3 = D1 Union D2

   3: Set M3 = M1 Union M2

再将A3, D3, M3进行互相的Intersection操作

   1: Set I_AD = A3 Intersection D3

   2: Set I_AM = A3 Intersection M3

   3: Set I_DM = D3 Intersection M3

然后再分别讨论I_AD, I_AM, I_DM中的元素的归属问题：

   1: I_AD: 

   2: A1D2 --> Temporary

   3: D1A2 --> Add[Modify]

   4:  

   5: I_DM:

   6: D1M2 --> [Impossible]

   7: M1D2 --> Delete

   8:  

   9: I_AM:

  10: A1M2 --> Add

  11: M2A2 --> [Impossible]

因此，I_DM中的元素应该归于Delete，而I_AM中的元素应该归于Add,  I_AD中的元素要具体分析其出处才能决定是不是归于Add。

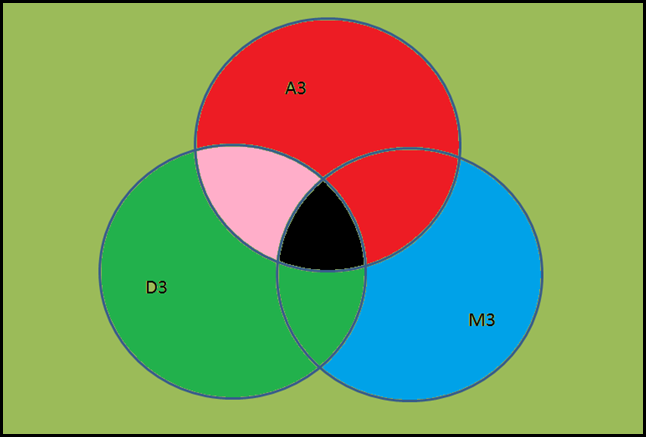
其中，三个圆区域分别代表A3, D3, M3区域；

黑色区域代表不可能出现的情况，红色区域代表集合A4, 绿色区域代表集合D4，而蓝色区域代表集合M4，粉色区域代表可能会属于A4M4的集合(具体取决于是A1D2还是A2D1)。