<知识整理>2019清北学堂提高储备D5

今天主讲图论。

前言：图的定义：图G是一个有序二元组(V,E)，其中V称为顶集(Vertices Set)，E称为边集(Edges set)，E与V不相交。它们亦可写成V(G)和E(G)。

一、图的存储：

　　1、邻接矩阵：

　　　　

　　2、邻接表：

　　　　数组模拟链表实现：记录每条边的终点、边权（如果有的话）、同一起点的上一条边的编号，并记录以每个点为起点的最后一条边的编号。

　　　　STL中的vector：记录以每个点为起点的边。

　　　　

　　　　　一些vector的细节：

　　　　　　vector 本质就是 c++ 模板库帮我们实现好的可以变长的数组

　　　　　　向一个数组（vector型） a 的末尾加入一个元素 x a.push_back(x)
　　　　　　询问 a 的长度 a.size()，询问a的真实长度a.capacity()
　　　　　　注意：vector 中元素下标从 0 开始，当需要变长时，变长一倍，因此需要额外的内存空间。

　　　　　　深入学习：https://www.cnblogs.com/zhonghuasong/p/5975979.html

　　　　代码：

　　　　邻接表：

const int N = ;//最多N个点/边

struct edge {
    int u, v, w, next;//起点，终点，边权，同起点的上一条边的编号
}edg[N];
int head[N]; //以每个点为起点的最后一条边的编号
int  n, m, cnt; //cnt: 边的总数

void add(int u, int v, int w)
{
    int e = ++cnt;
    edg[e] = (edge){u, v, w, head[u]};
    head[u] = e;
}
int main()
{
    cin >> n >> m; cnt = ;
    for (int u, v, w, i = ; i <= m; i++)
        cin >> u >> v >> w, add(u, v, w), odeg[u]++, ideg[v]++;
    return ;
}

　　　　vector:

 #include <bits/stdc++.h>

 using namespace std;

 const int N = ;

 struct edge {
     int u, v, w;
 };
 vector<edge> edg[N];
 int  n, m, cnt; //cnt: numbers of edges
 bool visited[N];

 void add(int u, int v, int w)
 {
     edg[u].push_back((edge){u, v, w});
 }
 void travel(int u, int distance)//遍历
 {
     cout << u << " " << distance << endl; visited[u] = true;
     for (int e = ; e < edg[u].size(); e++)
         if (!visited[edg[u][e].v])
             travel(edg[u][e].v, distance + edg[u][e].w);
 }
 int main()
 {
     cin >> n >> m; cnt = ;
     for (int u, v, w, i = ; i <= m; i++)
         cin >> u >> v >> w, add(u, v, w);
     return ;
 }
         

二、生成树

　　　　　　

　　最小生成树：给定一个 n 个点 m 条边的带权无向图，求一个生成树，使得生成

树中边权和的最小。

　　例题引入：

　　　

　　　　扩展（引用百度百科）：

　　

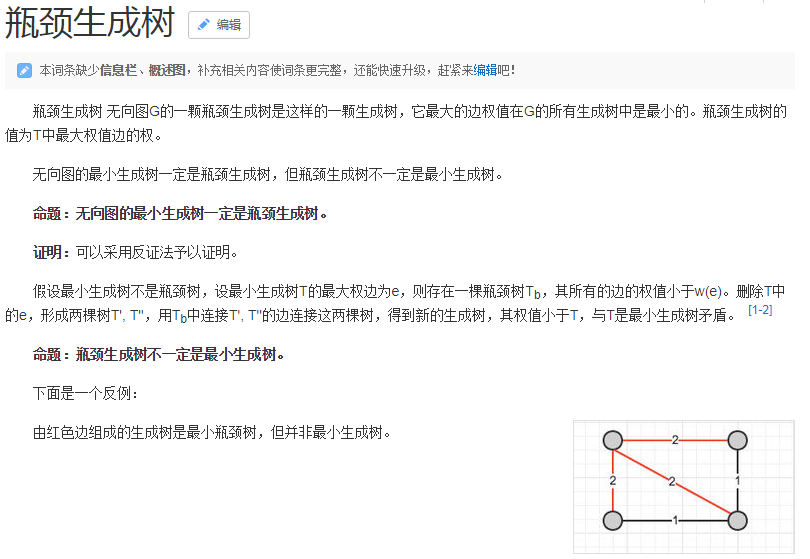
　　　　　只要求出最小生成树就好了。

　　求解最小生成树：

　　　生成树的本质：选取若干条边使得任意两点连通。

　　　各种求解算法的本质：贪心

　　　1、Kruskal算法（克鲁斯卡尔算法）：

　　　　　　将所有边按边权排好序，从最小的开始枚举：若加入该边后，会形成环（即边的端点已经连通），就忽略掉它，看下一条；否则加入该边，直至得到最小生成树（能得到的话）。查询两点连通情况：并查集。

　　　　时间复杂度：O（E log E）

　　　代码：

 #include <bits/stdc++.h>

 using namespace std;

 const int maxn = ;
 struct edge {
     int u, v, w;
 }edg[maxn];
 int n, m, p[maxn], ans = ;

 bool cmp(edge a, edge b)
     {return a.w < b.w;}
 int findp(int t)
     {return p[t] ? p[t] = findp(p[t]) : t;}
 bool merge(int u, int v)
 {
     u = findp(u); v = findp(v);
     if (u == v) return false;
     p[u] = v; return true;
 }
 int main()
 {
     cin >> n >> m;
     for (int i = , u, v, w; i <= m; i++)
         cin >> u >> v >> w, edg[i] = (edge){u, v, w};
     sort(edg + , edg + m + , cmp);

     for (int i = ; i <= m; i++)
         if (merge(edg[i].u, edg[i].v))
             ans = max(ans, edg[i]. w);
     cout << ans << endl;
 }

　　2、Prim算法（普里姆算法）：

　　　　　　以一点为最小生成树的根，找到一个到该最小连通块边权最小、不在该连通块里的点，并加入到该连通块，直到组成最小生成树。

　　　　时间复杂度：O(n²)

　　　　代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#define forup(i,n) for(int i=1;i<=n;i++)//偷懒
using namespace std;
int n,m;
int ma[][],bianli=,d[];
bool vis[];
int main()
{
    int x,y,z,tot=;
    cin>>n>>m;
    memset(ma,0x3f,sizeof(ma));//求最短性图论问题一般初始化为一个很大的数
    forup(i,m)
    {
        scanf("%d%d%d",&x,&y,&z);//去重边
        if(z<ma[x][y])
        ma[x][y]=ma[y][x]=z;
    }
    vis[]=;
    memset(d,0x3f,sizeof(d));
    d[]=;
    memset(vis,,sizeof(vis));//0蓝1白
    int stt_node,stt_dis;
    forup(i,n)
    {
        stt_dis=0x3f3f3f3f,stt_node=;
        for(int j=;j<=n;j++)
            if(!vis[j]&&d[j]<stt_dis)
            {
                stt_node=j;
                stt_dis=d[j];
            }
        vis[stt_node]=;
        tot+=stt_dis;
        for(int j=;j<=n;j++)
            if(!vis[j]&&d[j]>ma[j][stt_node])
            {
                d[j]=ma[j][stt_node];
            }
    }
    cout<<tot;
    return ;
}

三、路径

　　　最短路径问题：

　　　　　　

　　　

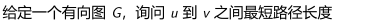
　　　最短路径算法本质思想：不断进行松弛操作（更新最短路操作）

　　　1、Floyd算法（弗洛伊德算法）：

　　　　

　　　　正确性：

　　　　　　

　　　　可求任意两点之间的最短路（多源最短路），时间复杂度O(n);

　　　负权环：

　　 

　　　　代码：

 int d[N][N], n, m;
 int main()
 {
     cin >> n >> m;
     for (int i = ; i <= n; i++)
         for (int j = ; j <= n; j++) d[i][j] = inf;
     for (int u, v, w, i = ; i <= m; i++)
         cin >> u >> v >> w, d[u][v] = min(d[u][v], w);

     for (int k = ; k <= n; k++)
         for (int i = ; i <= n; i++)
             for (int j = ; j <= n; j++)
                 d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
 }

　　　2、Bellman-Ford算法（贝尔曼-福特算法）

　　　　单源最短路算法，设源点为S

　　　　

　　　　正确性：

　　　　　　d[u]至少经过1条边，经过几条边，用几条边松弛后就能得到真实值。任意最短路经过不超过 n − 1 条边，n 次松弛足矣。

　　　因此不适用于有负权环的情况。（n为点数，m为边数）

　　　易知Bellman-Ford 算法中，如果 d(u) 在上一次全局更新中没有被更新，那么这一次全局更新中不必松弛 u 的出边（若能更新，上一次就不会不更新）。

　　代码：

 struct edge{
     int u, v, w;
 }edg[N];
 int d[N], n, m, S;
 int main()
 {
     cin >> n >> m >> S;
     for (int i = ; i <= n; i++) d[i] = inf;
     for (int u, v, w, i = ; i <= m; i++)
         cin >> u >> v >> w, edg[i] = (edge){u, v, w};

     d[S] = ;
     for (int i = ; i <= n; i++)
         for (int j = ; j <= m; j++)
         {
             int u = edg[j].u, v = edg[j].v, w = edg[j].w;
             d[v] = min(d[v], d[u] + w);
         }
 }

　　　3.SPFA算法（Shortest Path Faster Algorithm 翻译：最短路径快速算法（在一般情况下的确挺快的，只要不被针对））

　　　　贝尔曼-福特算法的队列优化形式，通过队列减少了很多冗余的计算，时间复杂度O（kE）(k是小常数，平均值为2）最糟糕的时间复杂度O(VE)（被针对的恐惧）　　

　　　　

　　　　

　　　　代码：

 struct edge{
     int u, v, w;
 };
 vector<edge> edg[N];
 int d[N], n, m, S;

 queue<int> Queue;
 bool inQueue[N];
 int cntQueue[N];

 void add(int u, int v, int w)
 {
     edg[u].push_back((edge){u, v, w});
 }
 int main()
 {
     cin >> n >> m >> S;
     for (int i = ; i <= n; i++) d[i] = inf;
     for (int u, v, w, i = ; i <= m; i++)
         cin >> u >> v >> w, add(u, v, w);

     d[S] = ; inQueue[S] = true; Queue.push(S);
     while (!Queue.empty())
     {
         int u = Queue.front(); Queue.pop(); inQueue[u] = false;
         for (int e = ; e < edg[u].size(); e++)
         {
             int v = edg[u][e].v, w = edg[u][e].w;
             if (d[v] > d[u] + w)
             {
                 d[v] = d[u] + w;
                 if (!inQueue[v])
                 {
                     Queue.push(v); ++cntQueue[v]; inQueue[v] = true;
                     if (cntQueue[v] >= n) {cout << "Negative Ring" << endl; return ;}//是负权环
                 }
             }
         }
     }
     for (int i = ; i <= n; i++)
         cout << d[i] << endl;
 }

　　　4.Dijkstra算法（ 迪杰斯特拉算法）

　　　　　　一个单源最短路算法。

　　　　　　知道d(u) 被更新成真实值之前，u 出边的松弛操作都无意义。以一个点为源点，设d[i]为i节点到根的最短距离。将d初始化（有与源点连边的为边的边权，否则为很大的数），找到最小的d[i]且i未被确定，将i节点标记为已确定最短路，并更新i节点出边终点的d。重复以上过程至所有点都被确定。

　　　　　　时间复杂度 O(n ² + m)

　　　　　　代码：

 #include <bits/stdc++.h>

 using namespace std;

 const int N = 1e5 + ;
 const int inf =  << ;

 struct edge{
     int u, v, w;
 };
 vector<edge> edg[N];
 int d[N], n, m, S;

 bool relaxed[N];

 void add(int u, int v, int w)
 {
     edg[u].push_back((edge){u, v, w});
 }
 int main()
 {
     cin >> n >> m >> S;
     for (int i = ; i <= n; i++) d[i] = inf;
     for (int u, v, w, i = ; i <= m; i++)
         cin >> u >> v >> w, add(u, v, w);

     d[S] = ;
     for (int i = ; i <= n; i++)
     {
         int u = ; while (relaxed[u]) ++u;//找到第一个没有被确定的点
         for (int j = ; j <= n; j++)//找到d[i]最短且未被确定的i
             if (!relaxed[j] && d[j] < d[u]) u = j;
         relaxed[u] = true;
         for (int e = ; e < edg[u].size(); e++)//进行松弛操作
         {
             int v = edg[u][e].v, w = edg[u][e].w;
             d[v] = min(d[v], d[u] + w);
         }
     }
     for (int i = ; i <= n; i++)
         cout << d[i] << endl;
 }

　　　　EX：Dijkstra堆优化

　　　利用小根堆的性质节省找到d[i]最小且未被确定的i的时间。

　　

　　　

　　　　代码：

 #include <bits/stdc++.h>

 using namespace std;

 const int N = 1e5 + ;
 const int inf =  << ;

 struct edge{
     int u, v, w;
 };
 vector<edge> edg[N];
 int d[N], n, m, S;

 bool relaxed[N];
 struct Qnode {
     int u, du;
     bool operator<(const Qnode &v)
         const {return v.du < du;}//不加const会出错
 };
 priority_queue<Qnode> PQueue;

 void add(int u, int v, int w)
 {
     edg[u].push_back((edge){u, v, w});
 }
 int main()
 {
     cin >> n >> m >> S;
     for (int i = ; i <= n; i++) d[i] = inf;
     for (int u, v, w, i = ; i <= m; i++)
         cin >> u >> v >> w, add(u, v, w);

     d[S] = ; PQueue.push((Qnode){S, });
     while (!PQueue.empty())
     {
         int u = PQueue.top().u; PQueue.pop();
         if (relaxed[u]) continue;
             //if edges staring from u are already relaxed, no need to relax again.
         relaxed[u] = true;
         for (int e = ; e < edg[u].size(); e++)
         {
             int v = edg[u][e].v, w = edg[u][e].w;
             if (d[v] > d[u] + w)
             {
                 d[v] = d[u] + w;
                 PQueue.push((Qnode){v, d[v]});
                 //if d(v) is updated, push v into PQueue
             }
         }
     }
     for (int i = ; i <= n; i++)
         cout << d[i] << endl;
 }

　　　　　　

三、DAG（有向无环图）

　　任意一个DAG一定有出度为0的点和入度为0的点。一个DAG删去一点后仍是DAG

　　1、拓补排序（topsort）

　　　　n个点的DAG一定存在拓补序列。

　　　　按照有向图中边的起点一定在终点之前的顺序给出一个可行的节点序列（多数不唯一）

　　　　换个角度：

　　　　

　　　实现：

　　1、

　　　　找到 DAG 中入度为 0 的点 u，u 可以放在当前 DAG 拓扑序末尾将 v 和与 v 有关的连边从 DAG 中删除

　　2、广搜：从入度为