洛谷P1077 摆花——题解

题目传送

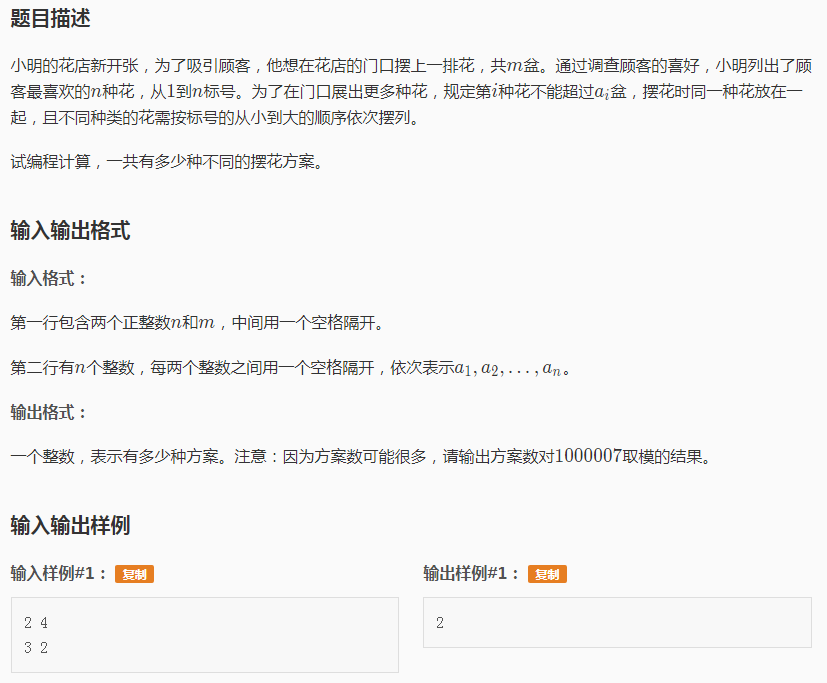
题目大意：有按顺序放的n种花，相同种类的花放一起，每种花最多放ai盆，共放了m盆花，求放花方案数。

求方案个数一般有以下思路：1、搜索；2、递推/动态规划；3、贪心；4、分治。。。

玄学估计发现，仅是可行解就有非常多的数量，显然搜索不行了。联想到“背包问题的方案总数”，猛然发现：这题不就相当于每个物品的重量都为1，最多选a_i个，求放满背包的方案总数吗？尝试写出状态：设dp[k][i]为只可能用前k种花、摆了i盆花的方案数，状态转移方程：(当i大于等于a_k时)dp[k][i]=dp[k-1][i-0]+dp[k-1][i-1]+..+dp[k-1][i-a_k];(当i小于a_k时）dp[k][i]=dp[k-1][i-0]+dp[k-1][i-1]+..+dp[k-1][0]。注意边界条件：a[1][i]=1,i=0，1，...，a₁，即只用第一种花摆花时是不能由上面的状态转移方程推出来的。

见AC代码：

 #include<iostream>
 #include<cstdio>

 using namespace std;

 int a[],n,m,dp[][],sum;

 const int mod=;

 int main()
 {
        scanf("%d%d",&n,&m);
        for(int i=;i<=n;i++)
            scanf("%d",&a[i]);
        for(int i=;i<=a[];i++) dp[][i]=;//初始化边界条件
        sum=a[];
        for(int k=;k<=n;k++)//花的种类
        {
            sum+=a[k];
            for(int i=;i<=sum&&i<=m;i++)//共要摆几个
            {
                for(int j=;j<=a[k]&&j<=i;j++)//第k种用几个
                    dp[k][i]+=dp[k-][i-j];
             dp[k][i]%=mod;
         }
     }
     cout<<dp[n][m];
     return ;
 }