QBXTD2上午

话说lyd昨天没讲完他的该死的贪心，所以今天继续讲

贪心思想是考虑AB是最快的人，CD是最慢的人，要把CD两个人送过河，只有两种方案，牵扯到四个人，并且n个规模的原问题化成了n-2个规模的子问题

那么最后有两个情况，四个人和三个人，如果是四个人就直接按刚才的方法搞一搞就好了，如果是三个人的话，就有两个方案，一个是A来回送，一个是AB一起操作，就是在两个之间取min就好了

贪心算法在骗分时的运用主要集中在两点：

1.贪心算法失效时该如何补救？

2.如何利用贪心算法来提升自己的一个暴力算法？

对于第一种情况， 我们可以采用贪心算法与随机化算法的结合（例如模拟退火）

在决策时有概率接受比当前情况差的方向

在搜索到结果时以一定概率跳出当前解，重新开始贪心

在贪心开始的时候，利用随机化选择多个起点开始贪心，取其最小值

2.贪心算法与搜索算法的结合

通过一定程度地选择次优解来计算答案,k-优搜索策略

结合贪心与搜索的策略，在大范围内贪心（用贪心剪枝），收束到小范围后开始搜索

分治：

分治分治，分而治之，分治算法就是将一个大问题划分为几个更小规模的问题并加以解决，通过解决子问题最后解决总问题。

分治算法在OI中的运用主要在两个方面：

1.基于二分查找、三分查找的运用

2.将题目划分为更细小的子问题的运用

我们将按顺序来讲解这两个方面

二分的本质是：在一个有序区间内确定一个边界，在边界的一边的元素满足某种性质，而另外一边不满足；

故二分经常用于解决如下类型的问题：

1.简单的二分查找

2.二分答案(即求一个单调函数在满足某个性质下的最值)

3.最值的最值(最常见的二分题类型)

差分前缀和加二分

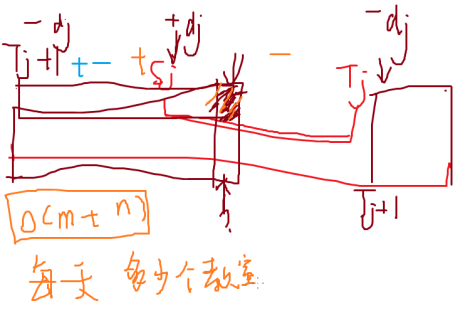
你现在需要给小A CntA 个自然数，给小B CntB 个自然数

但是给小A的自然数不能被x整除

同理给小B的自然数不能被y整除

请问需要给的最大的那个自然数最小是多少？

二分答案 v ，因为 a 不要被 x 整除的数，所以我们可以

先把 被 x 整除的数但不被 y 整除 给b，

再把 被 y 整除的数但不被 x 整除 给a。

然后剔除所有被 x*y 整除的数

剩下的数与 x 和 y 都互素，判一下能不能好好的分配就可以

三分

三分的难度是要比二分少的，因为三分函数的应用方面比较少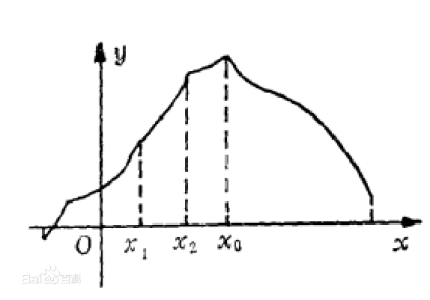

double search (double l, double r) {
    while (l+eps < r ) {
        m1 = ( * l + r) / ;
        m2 = (l + r * ) / ;
        double f1 = f(m1), f2 = f(m2);
        if (f1 < f2) l =f1;
        else r = f2;
    }
    return l;
}

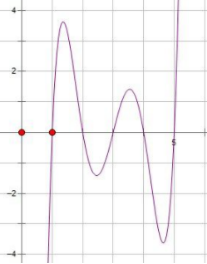
如果函数不是单峰的该怎么办？

分块

分块算法相当于是一个对于线段树和树状数组算法的下位替代品

由于其算法简单粗暴十分好写故广泛地运用于骗分领域（滑稽

下面是三个

1.给出一个长度为n的数列，以及m个操作，支持区间加法，单点查询

把长为n的数组分成√n块，对其中某一个区间[l,r]进行修改

1. l和r在同一块里    直接跑，复杂度不超过√n
2. l和r在相邻的块里    直接跑，复杂度不超过2√n
3. 其他情况    把l和r所在的块暴力增加，对中间的块打标记，复杂度不超过3√n

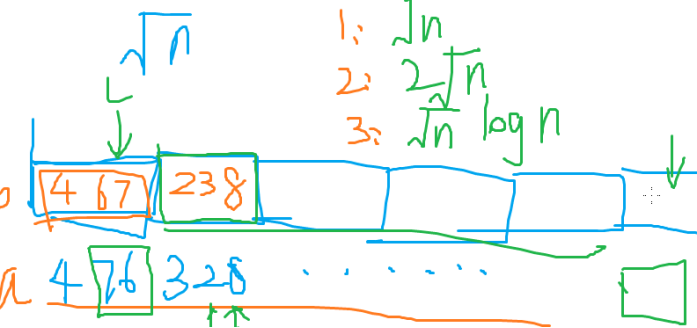
2. 给出一个长为n的数列以及m个操作，支持区间加法，并询问区间内小于等于某个数x的元素个数

　　每个块内部排序

1. l和r在同一块里    直接跑√n
2. l和r在相邻的块里    直接跑 2√n
3. 其他情况    两边暴力中间二分√n logn+2√

还有一个特别恶心的操作

3. 给出一个长为n的数列以及m个操作，支持区间开方，区间求和

我们发现一个longlong范围的数最多六次开方就会变成0或1

我们如果某个区间里每个数都是0或1就不用管他了

复杂度o(n√n+6n)

记录color[i]表示下标为i的球的颜色

Pre[i]表示前一个颜色为color[i]的球的颜色（前一个颜色和i相同的球）

引理：

如果Pre[i]<x<i，那么[x,i]区间内只有一种颜色为color[i]的球

所以：

查询[l,r]中有多少不同的颜色

只需要查询[l,r]种所有pre[i]<l的i的个数

对于修改，只需要对每一种颜色开一个set，修改的时候用类似于链表的方式将后驱的pre指向前驱就好了

或者暴力改也可以，qwq这个题修改比较水

搜索

最基础的是BFS和DFS