kmeans 聚类 k 值优化

kmeans 中k值一直是个令人头疼的问题，这里提出几种优化策略。

手肘法

核心思想

1. 肉眼评价聚类好坏是看每类样本是否紧凑，称之为聚合程度；

2. 类别数越大，样本划分越精细，聚合程度越高，当类别数为样本数时，一个样本一个类，聚合程度最高；

3. 当k小于真实类别数时，随着k的增大，聚合程度显著提高，当k大于真实类别数时，随着k的增大，聚合程度缓慢提升；

4. 大幅提升与缓慢提升的临界是个肘点；

5. 评价聚合程度的数学指标类似 mse，均方差，是每个类别的样本与该类中心的距离平方和比上样本数；

示例代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
# 1 数据可视化
cluster1 = np.random.uniform(0.5, 1.5, (2, 10))
cluster2 = np.random.uniform(3.5, 4.5, (2, 10))
X = np.hstack((cluster1, cluster2)).T
plt.figure()
plt.axis([0, 5, 0, 5])
plt.grid(True)
plt.plot(X[:, 0], X[:, 1], 'k.')
plt.show()

# 2 肘部法求最佳K值
K = range(1, 10)
mean_distortions = []
for k in K:
    kmeans = KMeans(n_clusters=k)
    kmeans.fit(X)
    mean_distortions.append(
        sum(
            np.min(
                cdist(X, kmeans.cluster_centers_, metric='euclidean'), axis=1))
        / X.shape[0])
plt.plot(K, mean_distortions, 'bx-')
plt.xlabel('k')
font = FontProperties(fname=r'c:\windows\fonts\msyh.ttc', size=20)
plt.ylabel(u'平均畸变程度', fontproperties=font)
plt.title(u'用肘部法确定最佳的K值', fontproperties=font)
plt.show()

输出手肘图

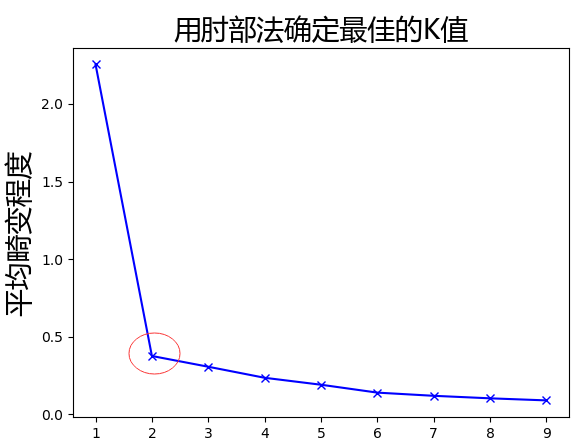
可以明显看出红色圆圈是个肘点。

缺点

1. 不是所有的数据都能呈现这样明显的肘点；

2. 单纯地以数据选择k值，可能脱离实际；

补充

在实际任务中，我们可能根据业务来确定 k 值，如区分男女，k=2，区分人种，k=3，黄黑白；

轮廓系数法

结合类内聚合度和类间分离度来评价聚类效果。

计算方法

1. 计算样本 i 到同簇内其他样本的平均距离 ai；【ai越小，说明该样本越应该被分到该簇，故可将 ai 视为簇内不相似度】

2. 计算簇内所有样本的 ai；

3. 计算样本 i 到其他簇内所有样本的平均距离 bi，并取min；【bi 视为 i 的类间不相似度，bi为i到其他类的所有bi中min，bi越大，越不属于其他类】

4. 样本 i 的簇内不相似度 ai 和类间不相似度 bi，计算轮廓系数

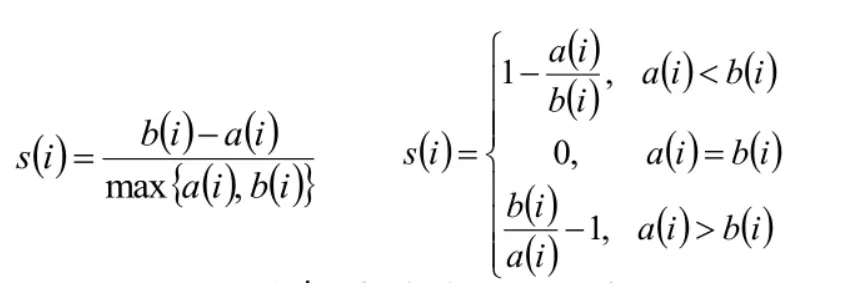
□ s_i 越接近1， 则说明样本 i 聚类合理。

□ s_i 越接近-1，说明样本 i 更适合聚到其他类

□ s_i 越接近0，则说明样本 i 在两个簇的边界上

这种方法计算量大，视情况使用。

参考资料：

https://blog.csdn.net/xiligey1/article/details/82457271

https://www.jianshu.com/p/f2b3a66188f1