杭州集训Day4

别问我为什么没有前三天，有时间再补~

60+60+50=170.

---

T1 . 坐等 memset0 _{( 1s 256MB )( 原题：洛谷CF1151E Number of Components )}

树链剖分是个喜欢逛讨论区的女孩子。
树链剖分看到有若干个小学生发的帖子，因为一些原因，这些帖子形
成了一条链。
其中第 i(1<=i< n)个帖子和第 i+1 个帖子用双向边相连
树链剖分举报了这些帖子，然后作为管理员的 memset0，决定对帖子
进行删除。
其中第 i 个帖子有一个小学生值 a[i].
但是， 因为 memset0 太强了， memset0 不屑于对小学生值在[l,r] 区
间内的帖子进行删除，只和谐掉其他帖子。（即，只保留小学生值[l,r]
的帖子）
现在，树链剖分想到一个问题，就是在这个保留下来的帖子里，联通
块的个数是多少。
问题还没完
我们把只保留小学生值[l,r]的帖子使得这些帖子的联通块的个数记
为 f(l,r)

求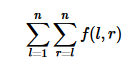

输入：
第一行一个正整数 n
第二行 n 个正整数 a[i]
输出
一行一个正整数，表示答案
样例输入
4
2 1 1 3
样例输出
11
对于 40%的数据 n <= 100
对于 60%数据 n <= 1000
对于 100%数据 n <= 100000,1<=a[i]<=n 且为正整数

emmmmmm

可以发现题目就是要我们求“权值在一个连续段里的数的连通块个数”

还不理解题意的话可以模拟下样例

考试时我是打了60分的n²暴力

i枚举权值的最大值:1~n

j枚举权值的最小值:i~1

然后模拟简单判断即可

然后是正解：

正解比我的暴力还短

就是1~n枚举累加(a[i]在权值范围内而a[i+1]不在权值范围内的种类数)

if(a[i]>a[i+1]) ans+=(ll)(a[i]-a[i+1])*(n-a[i]+1);

if(a[i]<a[i+1]) ans+=(ll)(a[i+1]-a[i])*a[i];

代码很简单就不贴了~

---

T2.吊打集训队 _{( 1s 256MB )( 原题：洛谷CF1146D Frog Jumping )}

树链剖分是一个喜欢膜巨佬的女孩子
一天树链剖分正在看 WXW 吊打集训队。
WXW 在数轴的 0 位置，其中数轴上的整点（包括 0） 上有一个队爷。
如果当前 wxw 在位置 k,则 wxw 可以跳到 k+a 或 k-b 位置。 wxw 只要
在一个位置上，就可以吊打该位置的集训队
但是 WXW 觉得这样很无聊，于是他搞了一个函数 f(X)表示 wxw 只能
在区间[0,x]中吊打集训队(wxw 只能在区间[0,x]里面，无法出来)，从 0
开始最多能吊打的队爷。
注： wxw 可以多次经过同一个位置，但同一个位置只算吊打一个队爷
wxw 想要求。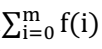

输入：
3 个正整数 m,a,b
输出
Wxw 想要求的结果
样例输入
7 5 3
样例输出
19
样例输入 2
6 4 5
样例输出 2
10
数据范围：
对于 20%的数据 m,a,b <= 100
对于 40%数据 m,a,b <= 1000
对于 60%的数据 m,a,b <= 100000
对于 100%的数据 m <= 1000,000,000 a,b <= 100,000

很容易想到找规律

在i<a时可以发现f(i)=1

在i>=a时WXW就可以跳出来吊打人了

当WXW可以不按原来的道路重新到达0时

WXW就开始循环了

比如当a=6,b=4时 WXW跳的路径为

0->6->2->8->4->0. f(i)=5.

再往后的话，WXW能到达任何2的倍数的点，即f(i)=(floor)(i/2);

（其实对于任意a,b，能任意到达的点是gcd(a,b)的倍数

因为ax+by=k 中k肯定是gcd(a,b)的倍数嘛）

再按照这个规律求剩下来的点

总的来说：

1.i<a时f(i)总和为a(当然如果n<a就可以输出n+1 return 0了

2.然后找到第一个使WXW开始循环的点i，用for循环找就可以了，因为这个点i不会超过2*max(a,b)

3.最后的点i到点n不难处理（但是代码难看，所以我还是推荐你们自己打，注意细节

对了，还有一件事：要开long long不然模拟赛中会60分（别问我怎么知道的www

上代码！！！（诶这三个字怎么这么大）

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n,a,b; ll ans;
int Gcd(int x,int y){ return y?Gcd(y,x%y):x; }
int main(){
//    freopen("ddjxd.in","r",stdin);
//    freopen("ddjxd.out","w",stdout);
    int i,w=; ll tot=; scanf("%d%d%d",&n,&a,&b); ans+=a;
    if(n<a) { printf("%d\n",n+); return ; }
    for(i=a;i;i++){
        while(w+a<=i){
            tot+=((i-w)/a);
            w+=((i-w)/a)*a;
            tot+=(w/b); w%=b;
            if(!w) break;
        } if(!w) break;
        ans+=tot; if(n==i) break;
    }
    if(!w){
        int p=Gcd(a,b); int j=n-n%p;
        tot=(ll)(i+j)*(j/p-i/p+)/;
        tot-=(ll)(j+p--n)*(j/p);
        ans+=tot+n-i+;
    }
    printf("%lld\n",ans);
    return ;
}

---

T3： Ynoi _{( 3s 256MB )}

树链剖分是个爱出题的女孩子。
ccz 出了一道数据结构题，结果太毒瘤了，树链剖分不会做
czz 也出了一道数据结构题，结果还是太毒瘤了，树链剖分还是不会
做
树链剖分也出了一道数据结构题，结果太水了，被大家秒了
后来， ccz， czz，树链剖分决定合出一道题
然后 ccz 觉得树链剖分太菜了，不屑于一起参与出题,于是去找 lxl 一
起出 Ynoi 了。
czz 也觉得树链剖分太菜了，但还是随手说了两个询问操作。
树链剖分:“那我干啥呢？”
czz：“你这么菜，出出来的题也是被大家秒掉。”
树链剖分：“好吧，那我造数据吧。”
结果由于树链剖分太菜了，她造的数据全是随机的。
现在有一个 1~n 的排列 a,
现在有以下操作
1 l r p 求 a[i]模 p 后的值在模 p 意义下的逆元的最大值(l <= i <= r)（保
证 p 为质数,p <= 100000）（如果 a[i]是 p 的倍数，则认为逆元是 0）
2 l r k 对于序列的第 i 个数，表示 i 号点， 从 a[i]向 i 连一条有向边，
求从点 i(l<=i<=r)开始出发恰好经过 k 条边， 到的点编号的最大值(可以
多次经过同一个点)。如果没有这样的点，输出-1
保证数据随机
输入：
第一行 两个正整数 n,m
表示序列长度和询问次数
第 2~m+1 行，每行若干个整数，表示一个操作
输出：
m 行，输出一个数， 询问的答案
样例输入
5 2
4 3 1 5 2
1 1 4 3
2 2 5 3
样例输出
2 4
数据范围
20%数据 n,m <= 100
50%数据 n,m <= 1000
100%数据 n,m <= 100000 ，所有输入的数均为正整数且小于等于 n。
1 <= l <= r <= n，且随机生成。

随机数据是这题的关键

但是时间复杂度我不会证呀，会证的可以在评论区发出来

然后其实这两个操作之间没有任何关系，恩

第一个的话需要for循环从p-1到0，枚举答案，

得出原数，再while循环加p，因为原数是膜p再求的

第二个的话需要for循环从n到1，枚举答案，

再用倍增或成环都可以

下面是代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+1e4;
int n,m,z,cnt,a[N],g[N],q[N],w[],f[N],fa[N][];
int rd(){
    int s=,ff=;
    char ww=getchar();
    while(ww<''||ww>''){
        if(ww=='-') ff=-;
        ww=getchar();
    }
    while(ww>=''&&ww<=''){
        s=s*+(ww-'');
        ww=getchar();
    }
    return s*ff;
}
int Pow(int x,int y,int p){
    int s=;
    while(y){
        if(y&) s=(ll)s*x%p;
        x=(ll)x*x%p; y>>=;
    }
    return s;
}
void Dfs(int x,int d){
    if(f[x]) { q[x]=d; return ; }
    f[x]=; Dfs(a[x],d+);
    q[x]=q[a[x]];
}
int Solve(int x,int s){
    for(int i=z;i>=;i--){
        if(s>=w[i])
            s-=w[i],x=fa[x][i];
    } return x;
}
int main(){
//    freopen("Ynoi.in","r",stdin);
//    freopen("Ynoi.out","w",stdout);
    n=rd(); m=rd(); z=log2(n); w[]=;
    for(int i=;i<=z;i++) w[i]=(w[i-]<<);
    for(int i=;i<=n;i++)
        a[i]=rd(),g[a[i]]=i,fa[i][]=a[i];
    for(int i=;i<=n;i++)
        if(!f[i]) Dfs(i,);
    for(int i=;i<=z;i++)
        for(int j=;j<=n;j++)
                fa[j][i]=fa[fa[j][i-]][i-];
    while(m--){
        int Opt=rd();
        if(Opt==){
            int l=rd(),r=rd(),p=rd();
            for(int i=p-;i>=;i--){
                int x=Pow(i,p-,p);
                while(g[x]<l||g[x]>r){
                    x+=p; if(x>n) break;
                }
                if(x<=n) {
                    printf("%d\n",i);
                    break;
                }
            }
        }
        else{
            int l=rd(),r=rd(),k=rd();
            for(int i=n;i>=;i--){
                int x=Solve(i,k%q[i]);
                if(x>=l&&x<=r){
                    printf("%d\n",i);
                    break;
                }
            }
        }
    }
    return ;
}

---

可以的话点个赞吧~谢谢~