模拟赛DAY 2 T2不老梦

【题目背景】

于万人中万幸得以相逢，刹那间澈净明通。

成为我所向披靡的勇气和惶恐，裂山海，堕苍穹。

爱若执炬迎风，炽烈而哀恸，诸般滋味皆在其中。

韶华宛转吟诵，苍凉的光荣，急景凋年深情难共。

——银临《不老梦》

【问题描述】

扶苏翻遍了歌单却没有找到一首歌能做这个题的题目背景，于是放上了扶苏最喜欢

的一首《不老梦》。

与 Day1 的第二题一样，今天的第二题依然是一道树论题。

我们定义一棵 n 个节点的树为一个有 n 个节点和 n-1 条边的无向连通图。

如果我们定义 u 是一颗树 T 的根，那么任意一个节点 v 到根的路径就是从 v 出发到

达点 u 的简单路径上所经过的点的点集。可以证明这样的简单路径有且仅有一条。

定义一个节点 x 是节点 y 的孩子，当且仅当 x 和 y 之间有边相连且 x 不在 y 到根的

路径中。如果 x 是 y 的孩子，那么定义 y 是 x 的家长节点。

如果我是 _rqy 那种毒瘤神仙的话，可能会问你每个节点的孩子数不超过 k 的 n 个节

点的带标号无根树一共有多少个，可惜这个问题我也不会，所以我不会问你这么毒瘤的

问题。

扶苏从一颗 n 个节点的树的 1 号节点出发，沿着树上的边行走。当然我们约定 1 号

节点是这棵树的根。他所行走的规定是：当扶苏在点 u 时，扶苏要么在 u 的孩子中选择

一个没有到达过得点 v 并行走到 v，要么选择回到 u的家长节点。

现在给每个节点一个权值 w，其中 i 号节点的权值为 wi。扶苏有一些石子，他想给

这棵树上的某一个节点放上石子。我们规定扶苏能在节点 u 放上石子当且仅当满足如下

条件：

1、扶苏当前在节点 u

2、对于 u 的所有孩子节点v，节点 v 被放上了 wv 颗石子。

但是，扶苏在任意时刻都可以取回任意节点的石子。

现在，扶苏想问问你对于每个节点，如果他想在 i 号节点上放 wi 颗石子，那么他一

开始需要准备多少石子。

【输入格式】

输入文件名为 yin.in。

输入文件中有且仅有一组数据，数据的第一行是一个整数 n 代表树的节点个数。

第二行有 n-1 个整数，第 i 个整数 pi 代表 i+1 号节点的家长节点的编号。

第三行有 n 个整数，第 i 个整数代表 wi。

【输出格式】

输出文件名为 yin.out。

输出一行 n 个整数，第 i 个整数代表想在 i 号节点上放 wi 颗石子需要准备的

石子个数。

 

【输入输出样例 1】

in

3

1 2

1 1 1

out

2 2 1

 

解释：

        

样例 1 的输入如左图，每个节点都需要放 1 块石头。

如果在 1 号节点放石头，则从一号点运动到 2号点，然后运动到 3 号点，在 3 号点上放一块

石头，返回 2 号点，在 2 号点上放一块石头，同时收回三号点的石头，然后返回 1 号点，将从 3 号点收回的石头放到 1 号点即可。一共需要两块石头。

在 2、3 号节点放石头的方案类似。 

 

【输入输出样例 2】

in

3

1 1

1 1 1

out

3 1 1

【输入输出样例 3】

in

6

1 1 2 3 4

3 14 1 5 12 15

out

21 20 13 20 12 15 

 

样例 3 的输入如左图。

先从 1 号节点运动至 3 号节点，再运动至 5 号节点，在 5 号节点上放置 12 块石子，然后返回 3 号节点，在 3 号节点上放置 1 块石子，收回五号节点的 12块石子，返回 1 号节点。

然后运动到 2 号节点，通过 4 号节点运动到 6 号节点，放下 15 颗石子，返回 4 号节点放下 5 颗石子，时树上有的石子数为5(4号)+15(6号)+1(3号)=21颗。然后收回 6 号节点的石子，返回 2 号节点，放下 14 颗石子，收回 4 号节点的，返回 1 号节点，在 1 号节点上放置 3 颗石子，即可达到在 1 号节点上放石子的目的。

可以验证最大花费为 21。其他节点的答案同理。

              

【题解】

测试点 1： 显然直接输出 w1 即可。期望得分 5 分。

测试点 2-5： 爆搜，搜出一个放石子的顺序，然后 O(n) 的 check 是否合法（看看是否父亲在儿子的前面）。时间复杂度 O(n!n)。期望得分 20 分。 

 

测试点 6-7：

注意到根据题目规定的走法，在进入一个节点以后，必须遍历完它的整个子树，否则一旦离开这个节点，再也无法进入这棵子树，从而导致该节点的某个孩子没能放上石子，导致这个节点不能放上石子。同时又有每个节点放上石子以后，它的子树的石子可以全部取回。设在节点 u 放石子需要有 ans_u 个石子，则放完 u 以后可以取回ans_u-w_u 个石子。

于是考虑影响问题答案的显然是从 u 进入每个孩子的顺序，由于最多有两个孩子，直接比较一下就可以知道先进入哪个孩子更优秀了。时间复杂度 O(n)，期望得分10 分。 

测试点 8-10：

延续上一组测试点的思路，由于只有最多 5 个孩子，可以直接爆搜选孩子的顺序，看看哪个更优秀。时间复杂度 O(n×x!)，其中 x=5。期望得分 15 分。 

测试点 11-14：

树高最多为 3。考虑进入第 3 层时由于不能回收石子，所以进入第三层的顺序无所谓，即对于第 2 层的每个节点 u,都有 ∑ _v∈cld[u]W_v。现在只需要考虑从 1 号节点进入它的所有孩子节点的顺序即可。 

考虑走完节点 u 的所有孩子 v 所需要的总石子数 c_u，显然是越少越好。证明如下：

走完所有孩子后，所花费的总石子数不变，设剩下的石子(也就是所需要的减去所花费的)为 ret，注意到当 c_u 最小的时候即是 ret 最小的时候。考虑当 ret ≥ wu的时候，直接用 ret 放下 u 上的石子，于是放石子在节点 u 的总花费就是 c_u，后者越小越好。 

当 ret < w_u 的时候，用剩下的石子放在 u 上，然后再额外放上去一些石子，这样做的花费是w_u+∑ _v∈cld[u]W_v，这显然是最小的花费，考虑当 c_u 越小 ret 才越小，c_u 取最小时显然能取到最优情况。 

综上，可以尽可能使 c_u 减小，来达到最优解。

那么问题变成了：

有 x 个商品，购买第 i 个物品需要手里有 ans_i 元钱，花费 w_i 元。求一个顺序使得购买所有商品所需要的钱数最少。

这个问题的最最优顺序是按照 ans_i-w_i 不升序购买，也就是差值越大越要先买。

证明：

设有两个物品 i,j，设 a_i=ans_i-w_i，a_j=ans_j-w_j。（放完i之后可以收回的石子数）且 a_i>a_j。考虑先买 i 再买 j 的花费是max(ans_i, w_i+ans_j) ①，同理先买 j 的花费是 max(ans_j, w_j+ans_i) ②。

提出 w，则 ①=w_i+max(a_i,ans_j)，②=w_j+max(a_j,ans_i)=w_j+max(a_j,a_i+w_i)=w_j+a_i+w_i。

考虑 ① 式的 max 如果取前面一项，则 ①=w_i+a_i<②，如果取后面一项则 ①=w_i+ans_j=w_i+a_j+w_j<②，于是无论怎么取，①式恒小于②式，于是先买 i 更优。数学归纳可得按照 ans_i-w_i 不升序购买最优。

于是按照这个顺序，排一遍序即可。期望得分 20 分。

测试点 15-20：

可以发现上面的结论同样适用于树高更高的情况，于是在 dfs 回溯的时候对子节

点排序，即可算出该节点的答案，期望得分 30 分。

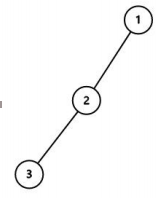
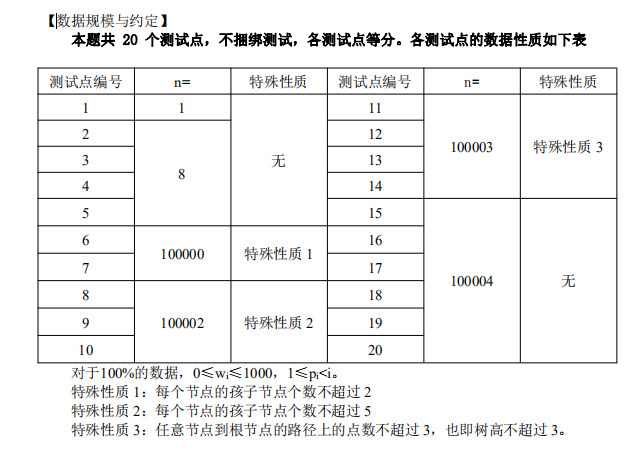
下面是代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read()
{
    ll ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=;

int n;
int mu[maxn],ans[maxn];
vector<int>son[maxn];

inline bool cmp(int a,int b)
{
    return (ans[a]-mu[a])>(ans[b]-mu[b]);
}//不升序 

void dfs(int u)
{
    for(int v=;v<son[u].size();v++)
    {
        dfs(son[u][v]);
    }//每一个节点都要搜
    sort(son[u].begin(),son[u].end(),cmp);//排序
    int ret=;//走完所有的孩子后剩下的石子
    for(int v=;v<son[u].size();v++)
    {
        if(ret>=ans[son[u][v]])//如果剩下的还够
        {
            ret-=ans[son[u][v]];//从剩下的里面减去
        }
        else//如果剩下的不够
        {
            ans[u]+=ans[son[u][v]]-ret;//更新ans
            ret=ans[son[u][v]]-mu[son[u][v]];
            //更新剩下的石子(就是可以取回的)
        }
    }
    ans[u]+=max(,mu[u]-ret);//更新答案
}

int main()
{
    n=read();
    for(int i=,x;i<=n;i++)
    {
        x=read();
        son[x].push_back(i);//标记x的儿子
    }
    for(int i=;i<=n;i++)
    {
        scanf("%d",mu+i);//mu+i表示mu[i]的地址
    }
    dfs();//开搜
    for(int i=;i<n;i++)
    {
        printf("%d ",ans[i]);
    }
    printf("%d\n",ans[n]);
    return ;
}