像计算机科学家一样思考python－第4章 案例研究：接口设计

系统环境　ubuntu18

4.1turtle模块

模块一开始导入turtle模块就报错了

 Python 3.6. (default, Apr   , ::)
 [GCC 7.3.] on linux
 Type "help", "copyright", "credits" or "license" for more information.
 >>> import turtle
 Traceback (most recent call last):
   File "<stdin>", line , in <module>
   File "/usr/lib/python3.6/turtle.py", line , in <module>
     import tkinter as TK
 ModuleNotFoundError: No module named 'tkinter'

从错误信息中可以看出：

turtle模块引用tkinter模块，但当前的运行环境没有tkinter模块文件，所以报错

解决办法：

注意：这里如果直接安装tkinter，会发现没有tkinter包

因为python-tk/python3-tk的类库需要在操作系统层面进行安装

这里把tkinter是什么，以及解决的过程描述的很清晰了。不再缀述，

Python3下提示No module named 'tkinter'＂问题解决

只说解决办法：

ubuntu16.04导入 pyplot报错：ModuleNotFoundError: No module named 'tkinter'

使用命令安装：

sudo apt-get install tcl-dev tk-dev python3-tk

开始安装：

 wangju@wangju-GL553VD:~$ sudo apt-get install tcl-dev tk-dev python3-tk
 [sudo] password for wangju:
 Reading package lists... Done
 Building dependency tree
 Reading state information... Done

完成安装：

再试一下：

问题解决

 Python 3.6. (default, Apr   , ::)
 [GCC 7.3.] on linux
 Type "help", "copyright", "credits" or "license" for more information.
 >>> import turtle
 >>> bob = turtle.Turtle()

出现了一个这样的窗口

创建文件mypolygon.py

代码如下：

 import tutle
 bob = turtle.Turtle()
 print(bob)
 turtle.mainloop()

运行mypolygon.py，结果如下：

 wangju@wangju-GL53VD:~$ python3 mypolygon.py
 <turtle.Turtle object at 0x7f44a642da58>

若要画一个朝右的角，在程序中（建立bob实例之后，调用mainloop之前）添加如下代码：

bob.fd()
bob.lt()
bob.fd()

运行这个程序时，将会看到bob先向东走，再向北走，身后留下两线段

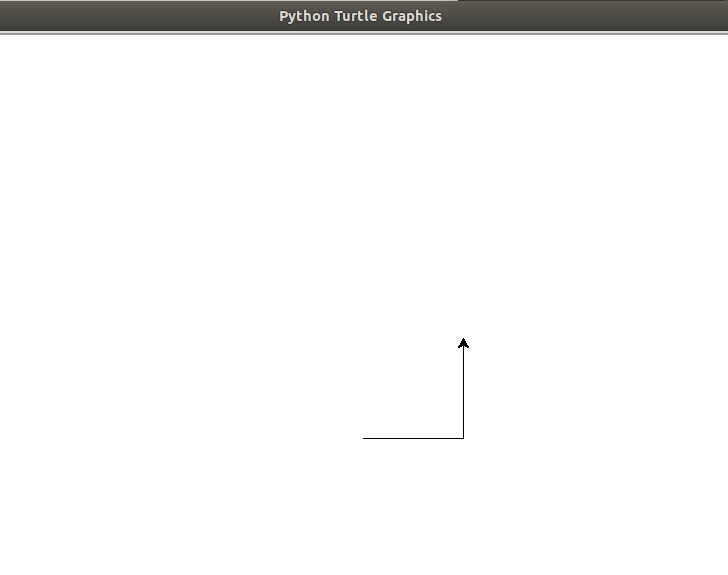
现在修改程序，画出一个正方形来

 bob.fd()
 bob.lt()

 bob.fd()
 bob.lt()

 bob.fd()
 bob.lt()

 bob.fd()

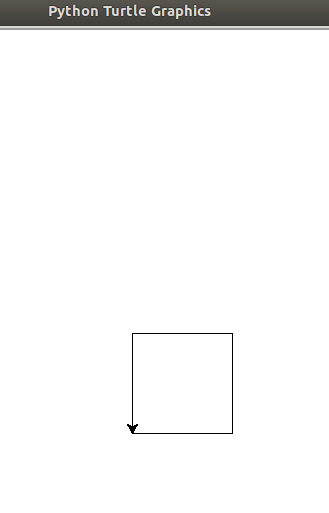
4.2简单重复

下面是使用for语句绘制正方形的程序

 for i in range():
     bob.fd()
     bob.lt()

for 语句的语法和函数定义类似。它也有一个以冒号结束的语句头，并有一个缩进的语句体。语句体可以包含任意数量的语句。

for语句也称为循环(loop)，因为执行流程会遍历语句体，之后从语句体的最开头重新循环执行。在这个例子里，，语句体执行了4次。

4.3练习

1.写一个函数 square，接受一个形参t，用来表示一只乌龟。利用乌龟来画一个正方形。

写一个函数调用,传入bob作为实参来调用square函数，并再运行一遍程序。

 import turtle
 bob = turtle.Turtle()

 def square(t):
     for i in range():
         t.fd()
         t.lt()

 #函数调用
 square(bob)
 turtle.mainloop()

2.给 square 函数再添加一个形参 length。修改函数内容，保证正方形的长度是length，并修改函数调用以提供这第二个实参。再运行一遍程序。使用不同的length值测试你的程序。

 import turtle
 bob = turtle.Turtle()

 def square(t,length):
     for i in range():
         t.fd(length)
         t.lt()

 square(bob,)
 turtle.mainloop()

3.复制 square函数，并命名为 polygon。再添加一个形参n并修改函数体以绘制一个正n边形。提示： 正n边形的拐角是360/n度。

def polygon(t,length,n):
    '''t bob,length 多边形每边的长度(bob每次移动的距离),n 正n边形'''
    for i in range(n):
        t.fd(length)
        t.lt(/n)

# square(bob,)
#正五边形
# polygon(bob,,)
#正3角形
polygon(bob,,)

4.写一个函数 circle接受代表乌龟的形参t，以及表示半径的形参 r ，并使用合适的长度和边数调用polygon画一个近似的圆。使用不同的r 值来测试你的函数。

提示： 思考圆的周长(circumference),并保证 length * n = circumference.

另一个提示： 如果你觉得bob太慢，可以修改bob.delay来加速。bob.delay代表每次行动之间的停顿，单位是秒。bob.delay = 0.01应该能让它跑得足够快。

解释：bob第一次移动的距离即圆形的半径r(圆上的任意一点到圆心的距离称为半径)。如图所示：

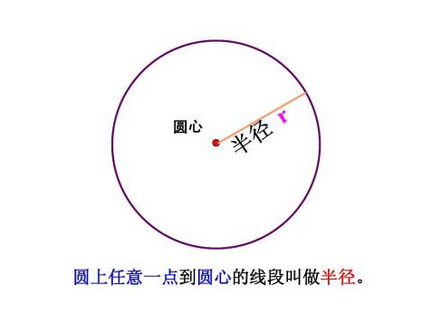
圆的周长公式：周长L=2πr（其中r为圆的半径，π为圆周率，通常情况下取3.14）

所以“ 合适的长度和边数”是

length * n = circumference

而

circumference＝2πr

所以 length * n＝2πr

如果不遵守这个规则，也可以画出圆，但是圆的半径却不能保证是r了，如图：

缩小r的值以后：

使用函数来编写程序：

 def circle(t,r,length,n):
     #先画出圆心到圆周的距离r
     t.fd(r)
     polygon(t,length,n)

 #半径100
 circle(bob,,12.5,)

5.给circle函数写一个更通用的版本，称为arc。增加一个形参 angle，用来表示画的圆弧的大小。这里angle的单位是度数，所以当 arc = 360时，则会画一个整圆。

这道题看不太懂是什么意思，我想是不是应该是这个意思，指定一个圆的周长，用angle表示。然后当周长是360时，会画出一个整圆（应该是angle＝350吧？）

 #angle 表示圆弧的长度
 def arc(t,angle):
     #随机生成一个在10～30之间的边长
     n = random.randint(,)

     length= angle/n

     t.fd(n)
     polygon(t,length,n)
 arc(bob,)

最后一道题感觉做的有问题，但是不想再深究了，因为主要不是为了解析这一道数学题目，而是为了学习书中的编程思想

4.4 封装

第一个练习要求把画正方形的代码放到一个函数定义中，并将乌龟bob作为实参传入，调用该函数。

最内侧的语句，fd和lt都缩进了两层，表示它们是在for 语句体内部，而for语句在函数定义的函数体内部。最后一行 square(bob)，又重新从左侧开始而没有缩进，这表明for语句和square函数都已经结束。

在函数体中，t引用的乌龟和bob引用的相同，所以 t.lt(90)和直接调用bob.lt(90)是一样的效果。在这种情况下为什么不直接把形参写成bob呢？原因是t可以是任何乌龟，而不仅仅是bob，所以可以再新建一只乌龟，并将它作为参数传入到square函数

 alice = turtle.Turtle()
 square(alice)

把一段代码用函数包裹起来，称为封装。封装的一个好处是，它给这段代码一个有意义的名称，增加了可读性。另一个好处是，当重复使用这段代码时，调用一次函数比复制粘贴代码要简易的多。

4.5泛化

给函数添加参数的过程称为泛化，因为它会让函数变得更通用

如果函数的形参比较多，很容易忘掉每一个具体是什么，或者忘掉它们的顺序，所以在Python中，调用函数时可以加上形参名称，这样是合法的，并且有时候会有帮助：

polygon(bob,n=,length=)设计

4.6接口设计

函数的接口是如何使用它的概要说明：它有哪些参数？这个函数做什么？它的返回值是什么？我们说一个接口“整洁”，是说它能够让调用者完成所想的的事情，而不需要处理多余的细节

在这个例子里，r属于函数的接口，因为它指定了所画的圆的基本属性。相对地，n则不那么适合，因为它说明的是如何画圆的细节信息。

所以与其弄乱接口，不如在代码内部根据周长来选择合适的n值

 def circle(t,r):
     circum=*math.pi*r
     n=int(circum/)+
     length=circum/n
     length= circum/n
     polygon(t,n,length)

现在多边形是的边数是一个接近circum/3的整数，所以每个边长近似是3，已经小到足够画出好看的圆形，但又足够大到不影响画线效率，并且可接受任何尺寸的圆。

关于圆形练习题，书中的答案：

 import turtle
 import math
 bob = turtle.Turtle()

 def polygon(t,n,length):
     angle=/n
     for i in range(n):
         t.fd(length)
         t.lt(angle)

 #version1
 def circle(t,r):
     circum=*math.pi*r
     n=
     length= circum/n
     polygon(t,n,length)

 #version2
 def circle(t,r):
     circum=*math.pi*r
     n=int(circum/)+
     length=circum/n
     length= circum/n
     polygon(t,n,length)

 circle(bob,)
 turtle.mainloop()

4.8一个开发计划

开发计划是一个写程序的过程。本章的案例分析中，我们使用的过程是“封装和泛化”。这个过程的具体步骤是：

1. 最开始写一些小程序，而不需要函数定义

2. 一旦程序运行成功，识别出其中一段完整的部分，将它封装到一个函数中，并加以命名。

3. 泛化这个函数，添加合适的形参。

4.重复步骤1到步骤3，直到得到一组可行的函数。复制粘贴代码，以避免重复输入（以及重复调试）

5.寻找可以使用重构来改善程序的机会。例如，如果发现程序中几处有相似的代码，可以考虑将它们抽取出来做一个合适的通用函数。

这个过程也有一些缺点——我们会在后面看到其他方式——但如果在开始编程时不清楚如何将程序分成适合的函数，这样做会带来帮助。这个方法能让你一边开发一边设计。

4.9文档字符串

文档字符串很简洁，但已经包含了其他人需要知道的关于函数的基本信息。它简明地解释了函数是做什么的（而不涉及如何实现的细节）。它解释了每个形参对函数行为的影响效果以及每个形参应有的类型（如果其类型并不显而易见）

编写这类文档是接口设计的重要部分。一个设计良好的接口，也应当很简单就能解释清楚； 如果你发现解释一个函数很困难，很可能表示该接口有改进的空间。

4.10调试

函数的接口，作用就像是函数和调用者之间签订的一个合同。调用者同意提供某些参数，而函数则同意使用这些参数做某种工作。

例如,polyline需要4个参数：t必须是一个Turtle； n必须是整数； length应当是个正数； 而则必须是一个数字，并且按照度数来理解。

这些需求被称为前置条件，因为它们应当在函数开始执行之前就保证为真。相对地，函数结束的时候需要满足的条件为后置条件。后置条件包含了函数预期的效果（如画出线段）以及任何副作用（如移动乌龟或者引起其他改变）

满足前置条件是调用者的职责。如果调用者违反了一个（文档说明清晰的！）前置条件，因而导致函数没有正确运行，则bug是在调用者，而不在函数本身。

如果前置条件都已经满足，但后置条件没有满足，那么bug就出现在函数本身。如果前置条件和后置条件都定义清晰，可以帮助调试。