[CSP-S模拟测试]:回文串（hash+二分）

题目描述

$ASDFZ$的机房中不仅有红太阳，还有蓝太阳和原谅色太阳。
有一天，太阳们来到机房，发现桌上有不知道哪个蒟蒻放上的问题：
令$F(A,B)$表示选择一个串$A$的非空前缀$S$和串$B$的非空后缀$T$使得将串$S$和串$T$拼起来之后是回文串的方案数。
现在给定两个串$A$和$B$，令$A_i$表示串$A$的第$i$长的后缀，$B_i$为串$B$的第$i$长的前缀。
有$Q$组询问，第$i$组询问给定$x_i$和$y_i$，对每组询问求$F(A_{x_i},B_{y_i})$的值。
太阳们非常强，自然不会把时间花在这种水题上。快来做做这个题呀。

---

输入格式

第一行一个字符串$str$，表示数据类型。
接下来的两行分别表示字符串$A$和$B$。
接下来一行一个正整数$Q$，表示询问的个数。
接下来$Q$行，每行两个正整数$x_i$和$y_i$。

---

输出格式

输出$Q$行，每行一个整数，表示这一组询问的答案。

---

样例

样例输入：

B
newionyzz
wyxioiwen
1
1 1

样例输出：

16

---

数据范围与提示

样例解释：

一共有以下$16$种方案：

$\{S=n,T=n\};\{S=n,T=en\};\{S=ne,T=n\};\{S=ne,T=en\};\{S=ne,T=wen\};\{S=new,T=en\};\{S=new,T=wen\};\{S=new,T=iwen\};\{S=new,T=ioiwen\};\{S=newi,T=wen\};\{S=newi,T=iwen\};\{S=newi,T=oiwen\};\{S=newio,T=iwen\};\{S=newio,T=oiwen\};\{S=newio,T=ioiwen\};\{S=newion,T=oiwen\};$

数据范围：

对于$100\%$的数据，字符串中只出现小写字母。

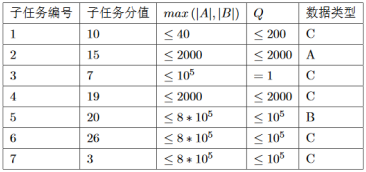
数据类型：$A:$随机数据，$B:$串$A$随机生成且$|B|\leqslant {10}^4$，$C:$无特殊性质。

---

题解

使用二分$+hash$判断以每个位置为中心延伸出去的回文串长度，这样会对一个区间的起点或终点的回文串个数产生$1$的贡献，差分一下最后前缀和一遍即可。
对于询问，注意到每次询问只要求一个区间内的$f$和$g$的和，前缀和即可。
每次通过二分$+hash$求$LCP$，得到最长的$l$。
时间复杂度：$\Theta((\max(|A|,|B|)+Q)\log(\max(|A|,|B|)))$。
最后$3$分显然是出题人想卡你自然溢出$hash$，所以就不要挣扎了。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
char A[800001],B[800001];
int q;
int lenA,lenB;
long long flag[800001],pre_A[800001],suc_A[800001],pre_B[800001],suc_B[800001],f[800001],g[800001],F[800001],G[800001];
void pre_work()
{
	flag[0]=1;
	for(int i=1;i<=800000;i++)
		flag[i]=flag[i-1]*13131%1000000007;
	for(int i=1;i<=lenA;i++)
	{
		pre_A[i]=(pre_A[i-1]*13131%1000000007+A[i]-'a'+1)%1000000007;
		suc_A[i]=(suc_A[i-1]*13131%1000000007+A[lenA-i+1]-'a'+1)%1000000007;
	}
	for(int i=1;i<=lenB>>1;i++)B[i]^=B[lenB-i+1]^=B[i]^=B[lenB-i+1];
	for(int i=1;i<=lenB;i++)
	{
		pre_B[i]=(pre_B[i-1]*13131%1000000007+B[i]-'a'+1)%1000000007;
		suc_B[i]=(suc_B[i-1]*13131%1000000007+B[lenB-i+1]-'a'+1)%1000000007;
	}
}
int preA(int L,int R){return(pre_A[R]-pre_A[L-1]*flag[R-L+1]%1000000007+1000000007)%1000000007;}
int sucA(int L,int R){return(suc_A[R]-suc_A[L-1]*flag[R-L+1]%1000000007+1000000007)%1000000007;}
int preB(int L,int R){return(pre_B[R]-pre_B[L-1]*flag[R-L+1]%1000000007+1000000007)%1000000007;}
int sucB(int L,int R){return(suc_B[R]-suc_B[L-1]*flag[R-L+1]%1000000007+1000000007)%1000000007;}
bool checkA(int L,int R)
{
	if(L<1||R>lenA)return 0;
	return preA(L,R)==sucA(lenA-R+1,lenA-L+1);
}
bool checkB(int L,int R)
{
	if(L<1||R>lenB)return 0;
	return preB(L,R)==sucB(lenB-R+1,lenB-L+1);
}
int find_A(int L,int R)
{
	int lft=1,rht=lenA;
	while(lft<rht-1)
	{
		int mid=(lft+rht)>>1;
		if(checkA(L-mid+1,R+mid-1))lft=mid;
		else rht=mid;
	}
	if(checkA(L-rht+1,R+rht-1))return L-rht+1;
	return L-lft+1;
}
int find_B(int L,int R)
{
	int lft=1,rht=lenB;
	while(lft<rht-1)
	{
		int mid=(lft+rht)>>1;
		if(checkB(L-mid+1,R+mid-1))lft=mid;
		else rht=mid;
	}
	if(checkB(L-rht+1,R+rht-1))return L-rht+1;
	return L-lft+1;
}
void pre_do_A()
{
	for(int i=1;i<=lenA;i++)
	{
		f[find_A(i,i)]++;
		f[i+1]--;
		if(A[i]==A[i+1])
		{
			f[find_A(i,i+1)]++;
			f[i+1]--;
		}
	}
	for(int i=1;i<=lenA+1;i++)
	{
		f[i]+=f[i-1];
		F[i]=F[i-1]+f[i];
	}
}
void pre_do_B()
{
	for(int i=1;i<=lenB;i++)
	{
		g[find_B(i,i)]++;
		g[i+1]--;
		if(B[i]==B[i+1])
		{
			g[find_B(i,i+1)]++;
			g[i+1]--;
		}
	}
	for(int i=1;i<=lenB+1;i++)
	{
		g[i]+=g[i-1];
		G[i]=G[i-1]+g[i];
	}
}
int LCP(int L,int R)
{
	int lft=0,rht=min(lenA-L+1,lenB-R+1);
	while(lft<rht-1)
	{
		int mid=(lft+rht)>>1;
		if(preA(L,L+mid-1)==preB(R,R+mid-1))lft=mid;
		else rht=mid;
	}
	if(preA(L,L+rht-1)==preB(R,R+rht-1))return rht;
	return lft;
}
int main()
{
	scanf("%s%s%s%d",A,A+1,B+1,&q);
	lenA=strlen(A+1),lenB=strlen(B+1);
	pre_work();
	pre_do_A();
	pre_do_B();
	while(q--)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		int len=LCP(x,y);
		printf("%lld\n",F[x+len]-F[x]+G[y+len]-G[y]+len);
	}
	return 0;
}

---

rp++