[CSP-S模拟测试]:Market（背包DP）

题目描述

　　在比特镇一共有$n$家商店，编号依次为$1$到$n$。每家商店只会卖一种物品，其中第$i$家商店的物品单价为$c_i$，价值为$v_i$，且该商店开张的时间为$t_i$。
　　$Byteasar$计划进行$m$次购物，其中第$i$次购物的时间为$T_i$，预算为$M_i$。每次购物的时候，$Byteasar$会在每家商店购买最多一件物品，当然他也可以选择什么都不买。如果购物的时间早于商店开张的时间，那么显然他无法在这家商店进行购物。
　　现在$Byteasar$想知道，对于每个计划，他最多能购入总价值多少的物品。请写一个程序，帮助$Byteasar$合理安排购物计划。
　　注意：每次所花金额不得超过预算，预算也不一定要花完，同时预算不能留给其它计划使用。

---

输入格式

　　第一行包含两个正整数$n,m$，表示商店的总数和计划购物的次数。
　　接下来$n$行，每行三个正整数$c_i,v_i,t_i$，分别表示每家商店的单价、价值以及开张时间。
　　接下来$m$行，每行两个正整数$T_i,M_i$，分别表示每个购物计划的时间和预算。

---

输出格式

　　输出$m$行，每行一个整数，对于每个计划输出最大可能的价值和。

---

样例

样例输入：

5 2
5 5 4
1 3 1
3 4 3
6 2 2
4 3 2
3 8
5 9

样例输出：

10
12

---

数据范围与提示

样例解释：

第一个计划可以在商店$2,3,5$各购买一件物品，总花费为$1+3+4=8$，总价值为$3+4+3=10$。
第二个计划可以在商店$1,2,3$各购买一件物品，总花费为$5+1+3=9$，总价值为$5+3+4=12$。

数据范围：

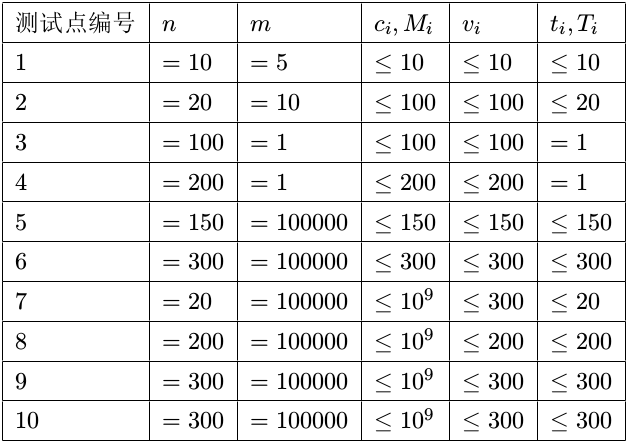
对于$100\%$的数据，$1\leqslant t_i,T_i\leqslant n$。

---

题解

对于正常的背包$DP$，我们都是设$dp[i][j]$表示选到第$i$个，背包空间为$j$所能获得的最大价值。

而对于这道题，背包空间很大，但是价值很小，所以我们不妨设$dp[i][j]$表示选到第$i$个，得到价值为$j$所消耗的最小背包空间。

对于时间，我们可以将物品和询问按时间排序，统一计算答案，然后在二分提取询问即可。

时间复杂度：$\Theta(n^2v+m\log m)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
struct rec{int c,v,t;}e[301];
struct node{int t,m,id;}q[100001];
int n,m;
int dp[100000];
int ans[100001];
bool cmp1(rec a,rec b){return a.t<b.t;}
bool cmp2(node a,node b){return a.t<b.t;}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		scanf("%d%d%d",&e[i].c,&e[i].v,&e[i].t);
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d",&q[i].t,&q[i].m);
		q[i].id=i;
	}
	sort(e+1,e+n+1,cmp1);
	sort(q+1,q+m+1,cmp2);
	memset(dp,0x3f,sizeof(dp));
	dp[0]=0;
	int j=1;
	for(int i=1;i<=m;i++)
	{
		while(j<=n&&e[j].t<=q[i].t)
		{
			for(int k=n*300;k>=e[j].v;k--)
				dp[k]=min(dp[k],dp[k-e[j].v]+e[j].c);
			for(int k=n*300;k;k--)
				dp[k]=min(dp[k],dp[k+1]);
			j++;
		}
		ans[q[i].id]=upper_bound(dp+1,dp+n*300+1,q[i].m)-dp-1;
	}
	for(int i=1;i<=m;i++)
		printf("%d\n",ans[i]);
	return 0;
}

---

rp++