【HDOJ6695】Welcome Party（multiset）

题意：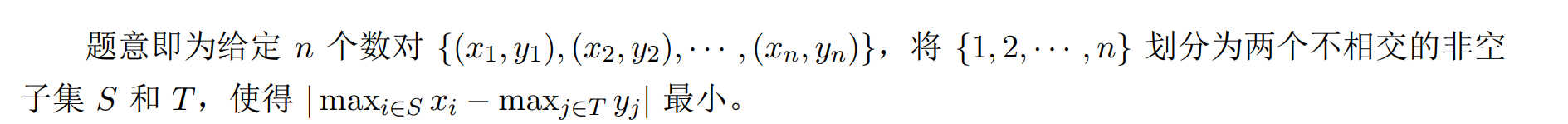

n<=1e5，x[i],y[i]<=1e18

思路：

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 typedef unsigned int uint;
 typedef unsigned long long ull;
 typedef pair<int,int> PII;
 typedef pair<ll,ll> Pll;
 typedef vector<int> VI;
 typedef vector<PII> VII;
 #define N  210000
 #define M  4100000
 #define fi first
 #define se second
 #define MP make_pair
 #define pi acos(-1)
 #define mem(a,b) memset(a,b,sizeof(a))
 #define rep(i,a,b) for(int i=(int)a;i<=(int)b;i++)
 #define per(i,a,b) for(int i=(int)a;i>=(int)b;i--)
 #define lowbit(x) x&(-x)
 #define Rand (rand()*(1<<16)+rand())
 #define id(x) ((x)<=B?(x):m-n/(x)+1)
 #define ls p<<1
 #define rs p<<1|1

 const ll MOD=1e9+,inv2=(MOD+)/;
       double eps=1e-;
       ll INF=1e18;
       int dx[]={-,,,};
       int dy[]={,,-,};

 struct arr
 {
     ll x,y;
 }a[N];

 multiset<ll> st;

 bool cmp(arr a,arr b)
 {
     return a.x<b.x;
 }

 ll read()
 {
    ll v=,f=;
    char c=getchar();
    while(c<||<c) {if(c=='-') f=-; c=getchar();}
    while(<=c&&c<=) v=(v<<)+v+v+c-,c=getchar();
    return v*f;
 }

 int main()
 {
     //freopen("1.in","r",stdin);
     //freopen("1.out","w",stdout);

     int cas;
     scanf("%d",&cas);

     while(cas--)
     {
        int n;
        scanf("%d",&n);
        rep(i,,n) a[i].x=read(),a[i].y=read();
        sort(a+,a+n+,cmp);
        st.clear();
        rep(i,,n) st.insert(a[i].y);
        int t=n+;
        ll mx=-,ans=1e18;
        per(i,n,)
        {
                while(t>&&a[t-].x>a[i].x)
                {
                    t--;
                    st.erase(st.find(a[t].y));
                    mx=max(mx,a[t].y);
                }
                st.erase(st.find(a[i].y));
                if(mx>=a[i].x) ans=min(ans,mx-a[i].x);
                 else
                 {
                     multiset<ll>::iterator it=st.lower_bound(a[i].x);
                     if(mx!=-) ans=min(ans,a[i].x-mx);
                     if(it!=st.end()) ans=min(ans,(*it)-a[i].x);
                     if(it!=st.begin())
                     {
                         it--;
                         if((*it)>mx) ans=min(ans,a[i].x-(*it));
                     }
                 }
             st.insert(a[i].y);
        }

        printf("%I64d\n",ans);

     }

     return ;
 }