机器学习之KNN原理与代码实现
KNN原理与代码实现
本文系作者原创，转载请注明出处:https://www.cnblogs.com/further-further-further/p/9670187.html
1. KNN原理
KNN（k-Nearest Neighbour）：K-近邻算法，主要思想可以归结为一个成语：物以类聚
1.1 工作原理
给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的 k （k <= 20）个实例，这 k 个实例的多数属于某个类，
就把该输入实例分为这个类。
https://www.cnblogs.com/ybjourney/p/4702562.html给出的例子很形象，这里借用一下。
如下图，绿色圆要被决定赋予哪个类，是红色三角形还是蓝色四方形？如果K=3，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类，
如果K=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。
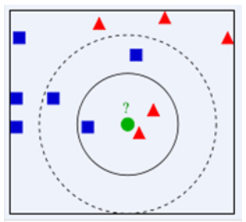
由此也说明了KNN算法的结果很大程度取决于K的选择。
1.2 欧氏距离公式
计算两个向量点xA和xB之间的距离
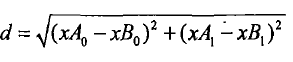
1.3 分类决策规则（如多数表决）
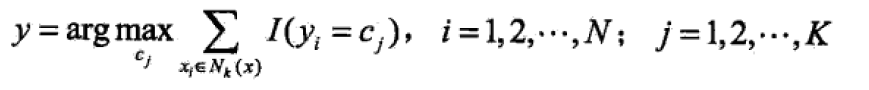
决定 类别
，
为指示函数，即当
时
为 1，否则
为0。
1.4 算法流程
对未知类别属性的数据集中的每个点依次执行以下操作：
1. 计算已知类别数据集中的点与当前点之间的距离；
2. 按照距离递增次序排序；
3. 选取与当前点距离最小的 k 个点；
4. 确定前 k 个点所在类别的出现频率；
5. 返回前 k 个点出现频率最高的类别作为当前点的预测分类；
2. 代码实现
python3.6
每个方法的作用，以及每行代码的作用，同样我都做了详细的注解。
希望大家最好自己能实现一下，特别是在运算时 list，array，matrix之间的关系以及运用场景，
只有在你自己实现时，才能理清这三者的作用以及关系。
2.1 输入数据
datingTestSet2.txt ：约会网站数据（三种类型：不喜欢的人，魅力一般的人，极具魅力的人）
8.326976 0.953952
7.153469 1.673904
1.441871 0.805124
13.147394 0.428964
1.669788 0.134296
10.141740 1.032955
6.830792 1.213192
13.276369 0.543880
8.631577 0.749278
12.273169 1.508053
3.723498 0.831917
8.385879 1.669485
4.875435 0.728658
4.680098 0.625224
15.299570 0.331351
1.889461 0.191283
7.516754 1.269164
14.239195 0.261333
0.000000 1.250185
10.528555 1.304844
3.540265 0.822483
2.991551 0.833920
5.297865 0.638306
6.593803 0.187108
2.816760 1.686209
12.458258 0.649617
0.000000 1.656418
9.968648 0.731232
1.364838 0.640103
0.230453 1.151996
11.865402 0.882810
0.120460 1.352013
8.545204 1.340429
5.856649 0.160006
9.665618 0.778626
9.778763 1.084103
4.932976 0.632026
2.216246 0.587095
14.305636 0.632317
12.591889 0.686581
3.424649 1.004504
0.000000 0.147573
8.533823 0.205324
9.829528 0.238620
11.492186 0.263499
3.570968 0.832254
1.771228 0.207612
3.513921 0.991854
4.398172 0.975024
4.276823 1.174874
5.946014 1.614244
13.798970 0.724375
10.393591 1.663724
3.007577 0.297302
1.031938 0.486174
4.751212 0.064693
3.692269 1.655113
10.448091 0.267652
10.585786 0.329557
1.604501 0.069064
3.679497 0.961466
3.795146 0.696694
2.531885 1.659173
9.733340 0.977746
6.093067 1.413798
7.712960 1.054927
11.470364 0.760461
2.886529 0.934416
10.054373 1.138351
9.972470 0.881876
2.335785 1.366145
11.375155 1.528626
0.000000 0.605619
4.126787 0.357501
6.319522 1.058602
8.680527 0.086955
14.856391 1.129823
2.454285 0.222380
7.292202 0.548607
8.745137 0.857348
8.579001 0.683048
2.507302 0.869177
11.415476 1.505466
4.838540 1.680892
10.339507 0.583646
6.573742 1.151433
6.539397 0.462065
2.209159 0.723567
11.196378 0.836326
4.229595 0.128253
9.505944 0.005273
8.652725 1.348934
17.101108 0.490712
7.871839 0.717662
8.262131 1.361646
9.015635 1.658555
9.215351 0.806762
6.375007 0.033678
2.262014 1.022169
5.677110 0.709469
11.293017 0.207976
6.590043 1.353117
4.711960 0.194167
8.768099 1.108041
11.502519 0.545097
4.682812 0.578112
12.446578 0.300754
12.908384 1.657722
12.601108 0.974527
3.929456 0.025466
9.751503 1.182050
3.043767 0.888168
4.391522 0.807100
11.695276 0.679015
7.879742 0.154263
5.613163 0.933632
9.140172 0.851300
4.258644 0.206892
6.799831 1.221171
8.752758 0.484418
1.123033 1.180352
10.833248 1.585426
3.051618 0.026781
5.308409 0.030683
1.841792 0.028099
2.261978 1.605603
11.573696 1.061347
8.038764 1.083910
10.734007 0.103715
9.661909 0.350772
9.005850 0.548737
0.000000 0.539131
5.757140 1.062373
9.164656 1.624565
1.318340 1.436243
14.075597 0.695934
10.107550 1.308398
7.960293 1.219760
6.317292 0.018209
12.664194 0.595653
2.906644 0.581657
2.388241 0.913938
6.024471 0.486215
7.226764 1.255329
4.183997 1.275290
11.850211 1.096981
11.661797 1.167935
3.574967 0.494666
0.000000 0.107475
7.937657 0.904799
3.365027 1.014085
0.000000 0.367491
13.860672 1.293270
10.306714 1.211594
7.228002 0.670670
4.508740 1.036192
0.366328 0.163652
3.299444 0.575152
0.573287 0.607915
9.183738 0.012280
7.842646 1.060636
4.750964 0.558240
11.438702 1.556334
8.243063 1.122768
7.949017 0.271865
7.875477 0.227085
9.569087 0.364856
7.750103 0.869094
0.000000 1.515293
3.396030 0.633977
11.916091 0.025294
0.460758 0.689586
13.087566 0.476002
4.589016 1.672600
8.397217 1.534103
5.562772 1.689388
10.905159 0.619091
1.311441 1.169887
10.647170 0.980141
0.000000 0.481918
8.503025 0.830861
0.436880 1.395314
6.127867 1.102179
12.112492 0.359680
1.264968 1.141582
6.067568 1.327047
8.010964 1.681648
3.791084 0.304072
11.773195 1.262621
8.339588 1.443357
2.563092 1.464013
5.954216 0.953782
9.288374 0.767318
3.976796 1.043109
8.585227 1.455708
1.271946 0.796506
0.000000 0.242778
0.000000 0.089749
11.521298 0.300860
1.139447 0.415373
5.699090 1.391892
2.449378 1.322560
0.000000 1.228380
3.168365 0.053993
10.428610 1.126257
2.943070 1.446816
10.441348 0.975283
12.478764 1.628726
5.856902 0.363883
2.476420 0.096075
1.826637 0.811457
4.324451 0.328235
1.376085 1.178359
5.342462 0.394527
11.835521 0.693301
12.423687 1.424264
12.161273 0.071131
8.148360 1.649194
1.531067 1.549756
3.200912 0.309679
8.862691 0.530506
6.370551 0.369350
2.468841 0.145060
11.054212 0.141508
2.037080 0.715243
13.364030 0.549972
10.249135 0.192735
10.464252 1.669767
9.424574 0.013725
4.458902 0.268444
0.000000 0.575976
9.686082 1.029808
13.649402 1.052618
13.181148 0.273014
3.877472 0.401600
1.413952 0.451380
4.248986 1.430249
8.779183 0.845947
4.156252 0.097109
5.580018 0.158401
15.040440 1.366898
12.793870 1.307323
3.254877 0.669546
10.725607 0.588588
8.256473 0.765891
8.033892 1.618562
10.702532 0.204792
5.062996 1.132555
10.772286 0.668721
1.892354 0.837028
1.019966 0.372320
15.546043 0.729742
11.638205 0.409125
3.427886 0.975616
11.246174 1.475586
0.000000 0.645045
0.000000 1.424017
8.242553 0.279069
8.700060 0.101807
0.812344 0.260334
2.448235 1.176829
13.230078 0.616147
0.236133 0.340840
11.155826 0.335131
11.029636 0.505769
2.901181 1.646633
3.924594 1.143120
2.524806 1.292848
3.527474 1.449158
3.384281 0.889268
0.000000 1.107592
11.898890 0.406441
3.529892 1.375844
11.442677 0.696919
10.308145 0.422722
8.540529 0.727373
7.156949 1.691682
0.720675 0.847574
0.229405 1.038603
3.399331 0.077501
6.157239 0.580133
1.239698 0.719989
6.036854 0.016548
5.258665 0.933722
12.393001 1.571281
9.627613 0.935842
11.130453 0.597610
8.842595 0.349768
10.690010 1.456595
5.714718 1.674780
3.052505 1.335804
0.000000 0.059025
9.945307 1.287952
2.719723 1.142148
11.154055 1.608486
2.687918 0.660836
10.037847 0.962245
12.404762 1.112080
10.237305 0.633422
4.745392 0.662520
4.639461 1.569431
3.149310 0.639669
13.406875 1.639194
6.068668 0.881241
9.477022 0.899002
3.897620 0.560201
5.463615 1.203677
3.369267 1.575043
5.234562 0.825954
0.000000 0.722170
12.979069 0.504068
5.376564 0.557476
13.527910 1.586732
2.196889 0.784587
10.691748 0.007509
1.659242 0.447066
8.369667 0.656697
13.157197 0.143248
8.199667 0.908508
4.441669 0.439381
9.846492 0.644523
0.019540 0.977949
8.253774 0.748700
6.038620 1.509646
6.091587 1.694641
8.986820 1.225165
11.508473 1.624296
8.807734 0.713922
0.000000 0.816676
8.889202 1.665414
3.178117 0.542752
7.013795 0.139909
9.605014 0.065254
1.230540 1.331674
10.412811 0.890803
0.000000 0.567161
9.699991 0.122011
0.000000 0.061191
4.455293 0.272135
3.020977 1.502803
8.099278 0.216317
1.157764 1.603217
10.105396 0.121067
11.230148 0.408603
9.070058 0.011379
0.566460 0.478837
0.000000 0.487300
8.956369 1.193484
1.523057 0.620528
2.749006 0.169855
9.235393 0.188350
10.555573 0.403927
6.956372 1.519308
0.636281 1.273984
3.574737 0.075163
9.032486 1.461809
5.958993 0.023012
2.435300 1.211744
10.539731 1.638248
7.646702 0.056513
20.919349 0.644571
1.424726 0.838447
6.748663 0.890223
2.289167 0.114881
5.548377 0.402238
6.057227 0.432666
10.828595 0.559955
11.318160 0.271094
13.265311 0.633903
0.000000 1.496715
6.517133 0.402519
4.934374 1.520028
10.151738 0.896433
2.425781 1.559467
9.778962 1.195498
12.219950 0.657677
7.394151 0.954434
8.518535 0.742546
2.798700 0.662632
0.637930 0.617373
10.750490 0.097415
0.625382 0.140969
10.027968 0.282787
9.817347 0.364197
0.646828 1.266069
3.347111 0.914294
11.816892 0.193798
0.000000 1.480198
10.945666 0.993219
10.244706 0.280539
2.579801 1.149172
2.630410 0.098869
11.746200 1.695517
8.104232 1.326277
12.409743 0.790295
12.167844 1.328086
3.198408 0.299287
16.055513 0.541052
7.138659 0.158481
4.831041 0.761419
10.082890 1.373611
10.066867 0.788470
8.129538 0.329913
3.012463 1.138108
3.720391 0.845974
0.773493 1.148256
10.962941 1.037324
0.177621 0.162614
3.085853 0.967899
8.426781 0.202558
1.825927 1.128347
2.185155 1.010173
7.184595 1.261338
0.000000 0.116525
8.901752 1.033527
2.451497 1.358795
3.213631 0.432044
3.974739 0.723929
9.601306 0.619232
8.363897 0.445341
6.381484 1.365019
0.000000 1.403914
9.609836 1.438105
9.904741 0.985862
7.185807 1.489102
5.466703 1.216571
0.000000 0.915898
4.575443 0.535671
3.277076 1.010868
10.246623 1.239634
2.341735 1.060235
3.201046 0.498843
6.066013 0.120927
8.829379 0.895657
15.833048 1.568245
13.516711 1.220153
0.664284 1.116755
6.325139 0.605109
8.677499 0.344373
8.188005 0.964896
9.414263 0.384030
9.196547 1.138253
10.202968 0.452363
2.119439 1.481661
13.635078 0.858314
0.083443 0.701669
9.149096 1.051446
1.933803 1.374388
14.115544 0.676198
8.933736 0.943352
2.661254 0.946117
0.988432 1.305027
2.063741 1.125946
2.220590 0.690754
6.424849 0.806641
1.156153 1.613674
3.032720 0.601847
3.076828 0.952089
0.000000 0.318105
7.750480 0.554015
10.958135 1.482500
10.222018 0.488678
2.367988 0.435741
7.686054 1.381455
11.464879 1.481589
11.075735 0.089726
3.543989 0.345853
8.123889 1.282880
4.331769 0.754467
0.120865 1.211961
6.116109 0.701523
7.474534 0.505790
8.819454 0.649292
6.802144 0.615284
12.666325 0.931960
8.636180 0.399333
11.730991 1.289833
8.132449 0.039062
10.296589 1.496144
7.583906 1.005764
9.777806 0.496377
8.833546 0.513876
4.907899 1.518036
8.362736 1.285939
9.084726 1.606312
14.164141 0.560970
9.080683 0.989920
6.522767 0.038548
3.690342 0.462281
3.563706 0.242019
1.065870 1.141569
6.683796 1.456317
1.712874 0.243945
13.109929 1.280111
11.327910 0.780977
4.545711 1.233254
3.367889 0.468104
8.326224 0.567347
8.978339 1.442034
5.655826 1.582159
8.855312 0.570684
6.649568 0.544233
3.966325 0.850410
1.924045 1.664782
6.004812 0.280369
0.000000 0.375849
9.923018 0.092192
2.389084 0.119284
13.663189 0.133251
11.434976 0.321216
0.358270 1.292858
9.598873 0.223524
6.375275 0.608040
11.580532 0.458401
5.319324 1.598070
4.324031 1.603481
2.358370 1.273204
0.000000 1.182708
12.824376 0.890411
1.587247 1.456982
8.510324 1.520683
10.428884 1.187734
8.346618 0.042318
7.541444 0.809226
2.540946 1.583286
9.473047 0.692513
0.352284 0.474080
0.000000 0.589826
12.405171 0.567201
4.126775 0.871452
0.034087 0.335848
1.177634 0.075106
0.000000 0.479996
0.994909 0.611135
11.053664 1.180117
0.000000 1.679729
2.495011 1.459589
11.516831 0.001156
9.213215 0.797743
5.332865 0.109288
0.000000 1.689771
0.000000 1.126053
12.640062 1.690903
2.693142 1.317518
3.328969 0.268271
7.193166 1.117456
6.615512 1.521012
8.000567 0.835341
4.017541 0.512104
13.245859 0.927465
5.970616 0.813624
11.668719 0.886902
4.283237 1.272728
10.742963 0.971401
12.326672 1.592608
0.000000 0.344622
0.000000 0.922846
10.602095 0.573686
10.861859 1.155054
1.229094 1.638690
0.410392 1.313401
14.552711 0.616162
14.178043 0.616313
14.136260 0.362388
0.093534 1.207194
10.929021 0.403110
11.432919 0.825959
9.134527 0.586846
5.071432 1.421420
11.460254 1.541749
11.620039 1.103553
4.022079 0.207307
3.057842 1.631262
7.782169 0.404385
7.981741 0.929789
4.601363 0.268326
2.595564 1.115375
10.049077 0.391045
3.265444 1.572970
11.780282 1.511014
3.075975 0.286284
1.795307 0.194343
11.106979 0.202415
5.994413 0.800021
9.706062 1.012182
10.582992 0.836025
7.038266 1.458979
0.023771 0.015314
12.823982 0.676371
3.617770 0.493483
8.346684 0.253317
6.104317 0.099207
16.207776 0.584973
6.401969 1.691873
2.298696 0.559757
7.661515 0.055981
6.353608 1.645301
10.442780 0.335870
3.834509 1.346121
10.998587 0.584555
2.695935 1.512111
3.356646 0.324230
14.677836 0.793183
1.551934 0.130902
2.464739 0.223502
1.533216 1.007481
12.473921 0.162910
6.491596 0.032576
10.506276 1.510747
4.380388 0.748506
13.670988 1.687944
8.317599 0.390409
0.000000 0.556245
0.000000 0.290218
10.095799 1.188148
0.860695 1.482632
1.557564 0.711278
10.072779 0.756030
0.000000 0.431468
7.140817 0.883813
11.384548 1.438307
3.214568 1.083536
11.720655 0.301636
6.374475 1.475925
5.749684 0.198875
3.871808 0.552602
8.336309 0.636238
9.710442 1.503735
1.532611 1.433898
9.785785 0.984614
2.633627 1.097866
9.238935 0.494701
1.205656 1.398803
3.124909 1.670121
7.935489 1.585044
12.746636 1.560352
10.732563 0.545321
3.977403 0.766103
4.194426 0.450663
9.610286 0.142912
4.797555 1.260455
1.615279 0.093002
4.614771 1.027105
0.000000 1.369726
0.608457 0.512220
6.558239 0.667579
12.315116 0.197068
7.014973 1.494616
8.822304 1.194177
10.086796 0.570455
7.241614 1.661627
4.602395 1.511768
7.434921 0.079792
10.467570 1.595418
9.948127 0.003663
2.478529 1.568987
5.938545 0.878540
0.000000 0.948004
5.559181 1.357926
9.776654 0.535966
3.092056 0.490906
0.000000 1.623311
4.459495 0.538867
8.334306 1.646600
11.226654 0.384686
3.904737 1.597294
7.038205 1.211329
9.836120 1.054340
1.990976 0.378081
9.005302 0.485385
1.772510 1.039873
0.458674 0.819560
10.003919 0.231658
0.520807 1.476008
10.678214 1.431837
4.425992 1.363842
12.035355 0.831222
10.606732 1.253858
1.568653 0.684264
2.545434 0.024271
10.264062 0.982593
9.866276 0.685218
0.142704 0.057455
9.853270 1.521432
6.596604 1.653574
2.602287 1.321481
10.411776 0.664168
7.083449 0.622589
2.080068 1.254441
0.522844 1.622458
10.362000 1.544827
3.412967 1.035410
6.796548 1.112153
4.092035 0.075804
2.763811 1.564325
12.547439 1.402443
5.708052 1.596152
4.558025 0.375806
11.642307 0.438553
3.222443 0.121399
4.736156 0.029871
10.839526 0.836323
4.194791 0.235483
14.936259 0.888582
3.310699 1.521855
2.971931 0.034321
9.261667 0.537807
7.791833 1.111416
1.480470 1.028750
3.677287 0.244167
2.202967 1.370399
5.796735 0.935893
3.063333 0.144089
11.233094 0.492487
1.965570 0.005697
8.616719 0.137419
6.609989 1.083505
1.712639 1.086297
10.117445 1.299319
0.000000 1.104178
9.824777 1.346821
1.653089 0.980949
18.178822 1.473671
6.781126 0.885340
8.206750 1.549223
10.081853 1.376745
6.288742 0.112799
3.695937 1.543589
6.726151 1.069380
12.969999 1.568223
2.661390 1.531933
7.072764 1.117386
9.123366 1.318988
3.743946 1.039546
2.341300 0.219361
0.541913 0.592348
2.310828 1.436753
6.226597 1.427316
7.277876 0.489252
0.000000 0.389459
7.218221 1.098828
8.777129 1.111464
2.813428 0.819419
2.268766 1.412130
6.283627 0.571292
7.520081 1.626868
11.739225 0.027138
3.746883 0.877350
12.089835 0.521631
12.310404 0.259339
0.000000 0.671355
2.728800 0.331502
10.814342 0.607652
12.170268 0.844205
6.698371 0.240084
3.632672 1.643479
10.059991 0.892361
1.887674 0.756162
8.229125 0.195886
7.817082 0.476102
12.277230 0.076805
10.055337 1.115778
3.596002 1.485952
2.755530 1.420655
7.780991 0.513048
0.093705 0.391834
8.481567 0.520078
3.865584 0.110062
9.683709 0.779984
10.617255 1.359970
7.203216 1.624762
7.601414 1.215605
1.386107 1.417070
9.129253 0.594089
1.363447 0.620841
3.181399 0.359329
13.365414 0.217011
4.207717 1.289767
4.088395 0.870075
3.327371 1.142505
1.303323 1.235650
7.999279 1.581763
2.217488 0.864536
7.751808 0.192451
14.149305 1.591532
8.765721 0.152808
3.408996 0.184896
1.251021 0.112340
6.160619 1.537165
1.034538 1.585162
0.000000 1.034635
2.355051 0.542603
6.614543 0.153771
10.245062 1.450903
3.467074 1.231019
7.487678 1.572293
4.624115 1.185192
8.995957 1.436479
11.564476 0.007195
3.440948 0.078331
1.673603 0.732746
4.719341 0.699755
10.304798 1.576488
2.086915 1.199312
6.338220 1.131305
8.254926 0.710694
16.067108 0.974142
1.723201 0.310488
3.785045 0.876904
2.557561 0.123738
9.852220 1.095171
3.679147 1.557205
9.789681 0.852971
14.958998 0.526707
11.182148 1.288459
7.528533 1.657487
5.253802 1.378603
13.946752 1.426657
15.557263 1.430029
12.483550 0.688513
2.317302 1.411137
10.069724 0.766119
5.792231 1.615483
4.138435 0.475994
12.929517 0.304378
9.378238 0.307392
8.361362 1.643204
7.939406 1.325042
10.735384 0.705788
11.592723 0.286188
10.098356 0.704748
9.299025 0.545337
11.158297 0.218067
16.143900 0.558388
10.971700 1.221787
0.000000 0.681478
3.178961 1.292692
17.625350 0.339926
1.995833 0.267826
10.640467 0.416181
9.628339 0.985462
4.662664 0.495403
5.754047 1.382742
0.000000 0.037146
9.334332 0.198118
3.846162 0.619968
10.685084 0.678179
4.752134 0.359205
0.697630 0.966786
10.365836 0.505898
0.461478 0.352865
11.339537 1.068740
5.420280 0.127310
3.469955 1.619947
8.517067 0.994858
8.306512 0.413690
2.628690 0.444320
0.000000 0.802985
0.000000 1.170397
7.298767 1.582346
7.331319 1.277988
9.392269 0.151617
5.541201 1.180596
15.149460 0.537540
5.515189 0.250562
7.728898 0.920494
11.318785 1.510979
3.574709 1.531514
7.350965 0.026332
7.122363 1.630177
1.828412 1.013702
10.117989 1.156862
11.309897 0.086291
8.342034 1.388569
0.241714 0.715577
10.482619 1.694972
9.289510 1.428879
4.269419 0.134181
0.000000 0.189456
0.817119 0.143668
1.508394 0.652651
9.359918 0.052262
10.052333 0.550423
11.111660 0.989159
11.265971 0.724054
10.383830 0.254836
3.878569 1.377983
13.679237 0.025346
10.526846 0.781569
0.000000 0.924198
4.106727 1.085669
8.118856 1.470686
7.796874 0.052336
2.789669 1.093070
6.226962 0.287251
10.169548 1.660104
0.000000 1.370549
7.513353 0.137348
8.240793 0.099735
14.612797 1.247390
3.562976 0.445386
3.230482 1.331698
3.612548 1.551911
0.000000 0.332365
3.931299 0.487577
14.752342 1.155160
10.261887 1.628085
2.787266 1.570402
15.112319 1.324132
5.184553 0.223382
3.868359 0.128078
3.507965 0.028904
11.019254 0.427554
3.812387 0.655245
11.056784 0.378725
8.826880 1.002328
11.173861 1.478244
11.506465 0.421993
7.798138 0.147917
10.155081 1.370039
10.645275 0.693453
9.663200 1.521541
10.790404 1.312679
2.810534 0.219962
9.825999 1.388500
1.421316 0.677603
11.123219 0.809107
13.402206 0.661524
1.212255 0.836807
1.568446 1.297469
3.343473 1.312266
5.400155 0.193494
3.818754 0.590905
7.973845 0.307364
9.078824 0.734876
0.153467 0.766619
8.325167 0.028479
7.092089 1.216733
5.192485 1.094409
10.340791 1.087721
2.077169 1.019775
10.151966 0.993105
0.046826 0.809614
11.221874 1.395015
14.497963 1.019254
3.554508 0.533462
3.522673 0.086725
14.531655 0.380172
3.027528 0.885457
1.845967 0.488985
10.226164 0.804403
10.965926 1.212328
2.129921 1.477378
0.000000 1.606849
9.489005 0.827814
0.000000 1.020797
0.000000 1.270167
6.556676 0.055183
9.959588 0.060020
7.436056 1.479856
0.404888 0.459517
9.952942 1.650279
15.600252 0.021935
2.723846 0.387455
0.513866 1.323448
0.000000 0.861859
7.280602 1.438470
9.161978 1.110180
0.991725 0.730979
7.398380 0.684218
12.149747 1.389088
9.149678 0.874905
9.666576 1.370330
3.620110 0.287767
5.238800 1.253646
14.715782 1.503758
14.445740 1.211160
13.609528 0.364240
3.141585 0.424280
0.000000 0.120947
0.454750 1.033280
0.510310 0.016395
3.864171 0.616349
6.724021 0.563044
4.289375 0.012563
0.000000 1.437030
3.733617 0.698269
2.002589 1.380184
2.502627 0.184223
6.382129 0.876581
8.546741 0.128706
2.694977 0.432818
3.951256 0.333300
9.856183 0.329181
2.068962 0.429927
3.410627 0.631838
9.974715 0.669787
10.650102 0.866627
9.134528 0.728045
7.882601 1.332446
输入数据集
2.2 KNN算法实现
myKNN.py
# -*- coding: utf-8 -*-
"""
Created on Mon Sep 17 15:58:58 2018
KNN(K-Nearest Neighbor) K-近邻算法
@author: weixw
""" import numpy as np
import operator
#输入：行测试数据集，训练数据集，标签数据集，用于选择最近邻居的数目
#功能：根据欧氏距离公式，找到与未知类别的测试数据距离最小的 k 个点，
# 以这 k 个点出现频率最高的类别座位测试数据的预测分类。
# 欧氏距离公式：测试数据与训练数据对应位置作差，平方和，然后开方
#输出：测试数据预测分类结果
def classify(testDataSet, trainingDataSet, labelList, k):
#训练数据集行数
trainingDataSetSize = trainingDataSet.shape[0]
#np.tile(testDataSet, (trainingDataSetSize,1)沿X轴复制1倍（相当于没有复制），再沿Y轴复制trainingDataSetSize倍，维数：1000*3
#欧氏距离公式实现
#1 测试数据 - 训练数据
diffMat = np.mat(np.tile(testDataSet, (trainingDataSetSize, 1)) - trainingDataSet)
#2 差平方（需要将matrix转化为数组，否则报错）
sqDiffMat = diffMat.A**2
#3 按行求和 axis = 0(默认按列) axis = 1(按行)
sqDistances = sqDiffMat.sum(axis = 1)
#4 开方
distances = sqDistances**0.5
#agrsort():从小到大排序，返回欧氏距离最小值对应的索引列表
sortedDistIndicies = distances.argsort()
#预测分类计数
predictClassCount = {}
#多数表决方式，选择 k 个欧氏距离最小值
for i in range(k):
#找到索引对应的标签值
voteLabel = labelList[sortedDistIndicies[i]]
#预测标签值字典，存储索引标签值预测次数
predictClassCount[voteLabel] = predictClassCount.get(voteLabel, 0) + 1
#对象按值逆向（由大到小）排序
# sorted(iterable[, cmp[, key[, reverse]]])
# itemgetter(1) 取第一项结果
sortedPredictClassCount = sorted(predictClassCount.items(), key = operator.itemgetter(1), reverse = True)
return sortedPredictClassCount[0][0] #输入：数据文件
#功能：加载文件，文件最后一列是标签数据，分离特征数据集与标签数据集
# 自动检测多少列特征数据并分离
#输出：特征数据集矩阵，标签数据集矩阵
def loadDataSet(fileName):
#特征数据列长度
numberFeat = len(open(fileName).readline().split('\t')) - 1
dataSet = []; labelSet = []
fr = open(fileName)
for line in fr.readlines():
lineArr = []
#去除收尾空格，然后分割每一列
curLine = line.strip().split('\t')
#保存每一列特征数据
for i in range(numberFeat):
lineArr.append(float(curLine[i]))
dataSet.append(lineArr)
labelSet.append(float(curLine[-1]))
return np.mat(dataSet), labelSet #输入：原始特征数据集
#功能：数据归一化，使每类数据都在同一范围内 (0, 1) 变化
# 归一化公式：newValue = (oldValue - min)/(max - min)
#输出：归一化后特征数据集，范围数组大小（分母）,列最小值数组
def autoNorm(dataMat):
#min(axis) 无参数：所有值中最小值；axis = 0：每列最小值；axis = 1：每行最小值
#求出每列最小值
minValsMat = dataMat.min(0)
#求出每列最大值
maxValsMat = dataMat.max(0)
#计算差值（对应位置相减）
rangesMat = maxValsMat - minValsMat
#归一化特征数据集初始化，维数：1000*3
normDataMat = np.zeros(np.shape(dataMat))
#原始数据集行数目
m = dataMat.shape[0]
#归一化公式分子实现
#np.tile(minVals, (m,1)沿X轴复制1倍（相当于没有复制），再沿Y轴复制m倍，维数：1000*3
normDataMat = dataMat - np.tile(minValsMat, (m, 1))
#归一化公式实现，求得归一化结果
normDataMat = normDataMat/np.tile(rangesMat, (m, 1))
return normDataMat, rangesMat, minValsMat #输入：特征数据集矩阵，标签数据集列表，测试数据与训练数据比例，用于选择最近邻居的数目
#功能：求出测试特征数据集预测分类结果
# 1.解析文件
# 2.通过ratio确定测试数据集
# 3.归一化
# 4.对每一行测试数据运用欧氏距离公式以及多数表决方式预测分类结果
# 5.求出整个测试数据集的预测分类结果
#输出：测试数据预测分类结果
def dataClassify(dataMat, labelList, ratio, k): #特征数据集归一化
normDataMat, rangesMat, minValsMat = autoNorm(dataMat)
#归一化特征数据集行数目
m = normDataMat.shape[0]
#测试数据集行数目（也就知道训练数据集行数）
testDataNum = int(m*ratio)
#预测分类错误计数
errorCount = 0.0
for i in range(testDataNum):
#求出测试数据集每行预测分类
classifierResult = classify(normDataMat[i, :], normDataMat[testDataNum:m, :], labelList[testDataNum:m], k)
print ("the classifier result is: %d, the real answer is: %d"% (classifierResult, labelList[i]))
#统计错误预测分类
if(classifierResult != labelList[i]):
errorCount += 1.0
print ("the total error count is %d"% errorCount)
print ("the total error rate is: %f"%(errorCount/float(testDataNum))) #绘制散点图
def drawScatter(filename):
import matplotlib.pyplot as plt
#加载文件，分离特征数据集和标签数据集
dataMat, labelList = loadDataSet(filename)
#矩阵转化为数组
dataArr = dataMat.A
#创建一副图画
plt.figure()
#保存标签类型相同的索引值（观察标签数据集，有3种不同类型）
label_idx1 = []; label_idx2 = []; label_idx3 = []
#遍历标签数组，索引，值
for index, value in enumerate(labelList):
if(value == 1):
label_idx1.append(index)
elif(value == 2):
label_idx2.append(index)
else:
label_idx3.append(index)
#scatter(x,y,s,maker,color,label)
#x,y必须是数组类型，s表示形状大小，maker:形状
plt.scatter(dataArr[label_idx1, 1], dataArr[label_idx1, 2], marker = 'x', color = 'm', label = 'no like', s = 30)
plt.scatter(dataArr[label_idx2, 1], dataArr[label_idx2, 2], marker = '+', color = 'c', label = 'like', s = 50)
plt.scatter(dataArr[label_idx3, 1], dataArr[label_idx3, 2], marker = 'o', color = 'r', label = 'very like', s = 15)
plt.legend(loc = 'upper right')
KNN算法实现
2.3 测试代码
# -*- coding: utf-8 -*-
"""
Created on Tue Sep 18 14:07:14 2018
测试KNN算法
@author: weixw
"""
import myKNN as mk
#前50%是测试数据，后50%作为训练数据
ratio = 0.5
#选择邻居数目
#errCount:31 errRate:6.2%
k = 4
#errCount:30 errRate:6.0%
#k = 8
#errCount:30 errRate:6.0%
#k = 12
#errCount:33 errRate:6.6%
#k = 16
#errCount:32 errRate:6.4%
#k = 20 fileName = 'datingTestSet2.txt'
#绘制数据散点图
mk.drawScatter(fileName)
#加载文件，分离特征数据集和标签数据集
dataMat, labelList = mk.loadDataSet(fileName)
#预测测试数据结果
mk.dataClassify(dataMat, labelList, ratio, k)
测试代码
2.4 运行结果
输入数据的散点图：
k = 4 ，ratio = 0.5（一半测试数据，一半训练数据）时分类结果：
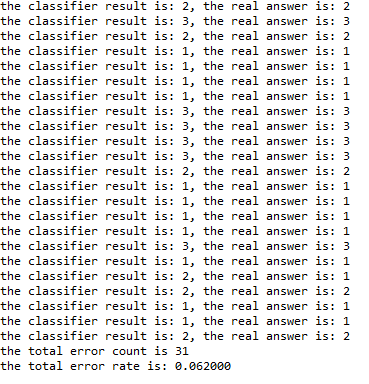
在 k为不同值时运行结果：
可以看出，并不是 k越大，正确率越高，会产生过拟合。
3. 优缺点
优点：
1. 简单，易于理解，易于实现，无需训练；
2. 精度高，对异常值不敏感；
缺点：
计算复杂度高，空间复杂度高。
4. 参考文献
《机器学习实战》
《统计学习方法》
知乎：https://www.zhihu.com/search?type=content&q=KNN
博客：https://www.cnblogs.com/ybjourney/p/4702562.html
不要让懒惰占据你的大脑，不要让妥协拖垮了你的人生。青春就是一张票，能不能赶上时代的快车，你的步伐就掌握在你的脚下。
机器学习之KNN原理与代码实现的更多相关文章
- 机器学习之AdaBoost原理与代码实现
AdaBoost原理与代码实现 本文系作者原创,转载请注明出处: https://www.cnblogs.com/further-further-further/p/9642899.html 基本思路 ...
- 机器学习之决策树三-CART原理与代码实现
决策树系列三—CART原理与代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/9482885.html ID ...
- 机器学习之决策树一-ID3原理与代码实现
决策树之系列一ID3原理与代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/9429257.html 应用实 ...
- 图机器学习(GML)&图神经网络(GNN)原理和代码实现(前置学习系列二）
项目链接:https://aistudio.baidu.com/aistudio/projectdetail/4990947?contributionType=1 欢迎fork欢迎三连!文章篇幅有限, ...
- 机器学习之决策树二-C4.5原理与代码实现
决策树之系列二—C4.5原理与代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/9435712.html I ...
- 机器学习之KNN算法
1 KNN算法 1.1 KNN算法简介 KNN(K-Nearest Neighbor)工作原理:存在一个样本数据集合,也称为训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一数据与所属 ...
- Python机器学习算法 — KNN分类
KNN简介 K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一.KNN分类算法属于监督学习. 最简单最初级的分类器是将全部的训练 ...
- 【机器学习】kNN
机器学习算法--kNN 目录 机器学习算法--kNN 1. 算法原理 2. 算法实现 2.1 kd-tree构造 2.2 kd-tree查询 2.3 kNN算法实现 3. 算法测试 Ref 1. 算法 ...
- 【机器学习】算法原理详细推导与实现(六):k-means算法
[机器学习]算法原理详细推导与实现(六):k-means算法 之前几个章节都是介绍有监督学习,这个章解介绍无监督学习,这是一个被称为k-means的聚类算法,也叫做k均值聚类算法. 聚类算法 在讲监督 ...
随机推荐
- linux系统版本查看
Linux下如何查看版本信息, 包括位数.版本信息以及CPU内核信息.CPU具体型号等等,整个CPU信息一目了然. 1.# uname -a (Linux查看版本当前操作系统内核信息) Lin ...
- java常用的框架介绍
一.SpringMVC http://blog.csdn.net/evankaka/article/details/45501811 Spring Web MVC是一种基于Java的实现了Web MV ...
- 深入javascript的主流的模块规范
文章首发于sau交流学习社区 一.前言 目前主流的模块规范: 1.UMD通用模块 2.CommonJs 3.es6 module 二.UMD模块(通用模块) (function (global, fa ...
- org.springframework.cache.interceptor.SimpleKey cannot be cast to java.lang.String
springboot整合redis时,使用@Cacheable注解,如果方法的key参数为空,就会报org.springframework.cache.interceptor.SimpleKey ca ...
- css属性分类介绍
css属性分类介绍 CSS分类目录 文本/字体/颜色 文本相关 字体相关 颜色相关 背景相关 大小/布局 大小属性 margin 外边距 padding 内边距 border 边框 position ...
- [开源]MasterChief 快速开发辅助类库
C# 开发辅助类库,和士官长一样身经百战且越战越勇的战争机器,能力无人能出其右. GitHub:MasterChief 欢迎Star,欢迎Issues: 项目架构思维导图: 目录 1. 数据库访问 2 ...
- vscode restclient 插件
使用步骤: 1.vscode 安装restclient 扩展 2.创建 .http 或 .rest 文件 ,编写相应内容 同一个文件内 可以通过 ### 分割多个请求 可以通过 @hostname ...
- .net mvc + layui做图片上传（一）
图片上传和展示是互联网应用中比较常见的一个功能,最近做的一个门户网站项目就有多个需要上传图片的功能模块.关于这部分内容,本来功能不复杂,但后面做起来却还是出现了一些波折.因为缺乏经验,对几种图片上传的 ...
- 简述Java变量和强制转换类型
简述Java变量和强制转换类型 java变量 1. java变量 变量:顾名思义,就是在java执行程序过程中可以发生改变的量,就好比方程式中的未知数X一样. 变量的内存分配过程 int a ; // ...
- Windows Server 2016-Netdom Join之客户端加域(二)
上章节我们介绍了如何通过图形化界面实现用户加域操作,本章节为大家简单介绍如何通过netdom join命令实现计算机加域操作.具体信息如下: 将工作站或成员服务器加入域.将计算机加入域的行为会为域中的 ...