最小生成树之Kruskal(克鲁斯卡尔)算法

学习最小生成树算法之前我们先来了解下下面这些概念：

　　树（Tree）：如果一个无向连通图中不存在回路，则这种图称为树。

　　生成树 （Spanning Tree）：无向连通图G的一个子图如果是一颗包含G的所有顶点的树，则该子图称为G的生成树。生成树是连通图的极小连通子图。这里所谓极小是指：若在树中任意增加一条边，则将出现一条回路；若去掉一条边，将会使之变成非连通图。

　　最小生成树（Minimum Spanning Tree，MST）：或者称为最小代价树Minimum-cost Spanning Tree:对无向连通图的生成树，各边的权值总和称为生成树的权，权最小的生成树称为最小生成树。常用于网络构建等建设性问题的优化。

构成生成树的准则有三条：

　　1、 必须只使用该网络中的边来构造最小生成树。

　　2、必须使用且仅使用n-1条边来连接网络中的n个顶点

　　3、不能使用产生回路的边。

　　构造最小生成树的算法主要有：克鲁斯卡尔（Kruskal）算法和普利姆（Prim）算法他们都遵循以上准则。

　　克鲁斯卡尔算法的基本思想是以边为主导地位，始终选择当前可用（所选的边不能构成回路）的最小权植边。所以Kruskal算法的第一步是给所有的边按照从小到大的顺序排序。这一步可以直接使用库函数qsort或者sort。接下来从小到大依次考察每一条边（u，v）。

具体实现过程如下：

　　1、设一个有n个顶点的连通网络为G（V,E），最初先构造一个只有n个顶点，没有边的非连通图T={V,空}，图中每个顶点自成一格连通分量。

　　2、在Ｅ中选择一条具有最小权植的边时，若该边的两个顶点落在不同的连通分量上，则将此边加入到Ｔ中；否则，即这条边的两个顶点落到同一连通分量      上，则将此边舍去（此后永不选用这条边），重新选择一条权植最小的边。

　　3、如此重复下去，直到所有顶点在同一连通分量上为止。

 import java.util.ArrayList;
 import java.util.Collections;
 import java.util.HashMap;
 import java.util.HashSet;
 import java.util.List;
 import java.util.Map;
 import java.util.Set;

 public class Kruskal {
     private final List<Edge> edgeList;
       private final int n;//总顶点数

       private Set<Edge> T = new HashSet<>();//生成树的边集
       private Map pntAndNode = new HashMap();

       public Set<Edge> getT() {
         buildMST();
         return T;
       }

       public Kruskal(List<Edge> edgeList, int n) {
         this.edgeList = edgeList;
         //为每个顶点建立一个并查集的点
         for (Edge edge : edgeList) {
           pntAndNode.put(edge.getStart(), new UnionFind.UFNode());
           pntAndNode.put(edge.getEnd(), new UnionFind.UFNode());
         }
         this.n = n;
       }

       public static void main(String[] args) {
         List<Edge> edgeList = build();
         Kruskal obj = new Kruskal(edgeList, 5);
         // obj.buildMST();
         for (Edge e : obj.getT()) {
           System.out.println(e);
         }
       }

       private static List<Edge> build() {
         List<Edge> l = new ArrayList<>();
         l.add(new Edge("C", "D", 1));
         l.add(new Edge("C", "A", 1));
         l.add(new Edge("C", "E", 8));
         l.add(new Edge("A", "B", 3));
         l.add(new Edge("D", "E", 3));
         l.add(new Edge("B", "C", 5));
         l.add(new Edge("B", "E", 6));
         l.add(new Edge("B", "D", 7));
         l.add(new Edge("A", "D", 2));
         l.add(new Edge("A", "E", 9));

         return l;
       }

       /*构建MST的核心方法*/
       private void buildMST() {
         Collections.sort(edgeList);//排序
         //迭代
         for (Edge e : edgeList) {
           if (!ok(e))
             continue;
           //确认过了，就把边都加入
           T.add(e);

           if (T.size() == n - 1)
             return;//生成树的边数==总顶点数-1 =》 所有点都已经连接
         }
       }

       //并查集中查询e  的起点和终点是否在一个集中
       private boolean ok(Edge e) {
         UnionFind.UFNode x = (UnionFind.UFNode) pntAndNode.get(e.getStart());
         UnionFind.UFNode y = (UnionFind.UFNode) pntAndNode.get(e.getEnd());
         if (UnionFind.find(x) != UnionFind.find(y)) {//在不同的集中
           UnionFind.union(x, y);//合并并返回true
           return true;
         }
         return false;
       }

 }

　　最关键的地方在于“连通分量的查询和合并”，需要知道任意两个点是否在同一连通分量中，还需要合并两个连通分量。这个问题正好可以用并查集完美的解决

　　并查集（Union-Find set）这个数据结构可以方便快速的解决这个问题。基本的处理思想是：初始时把每个对象看作是一个单元素集合；然后依次按顺序读入联通边，将连通边中的两个元素合并。在此过程中将重复使用一个搜索（Find）运算，确定一个集合在那个集合中。当读入一个连通边（ｕ，ｖ）时，先判断ｕ和ｖ是否在同一个集合中，如果是则不用合并；如果不是，则用一个合并（Union）运算把ｕ、ｖ所在集合合并，使得这两个集合中的任意两个元素都连通。因此并查集在处理时，主要用到搜索和合并两个运算。

　　为了方便并查集的描述与实现，通常把先后加入到一个集合中的元素表示成一个树结构，并用根结点的序号来表示这个集合。因此定义一个parent[n]的数组，parent[i]中存放的就是结点ｉ所在的树中结点ｉ的父亲节点的序号。例如，如果parent[4]=5，就是说４号结点的父亲结点是５号结点。约定：如果ｉ的父结点（即parent[i]）是负数，则表示结点ｉ就是它所在的集合的根结点，因为集合中没有结点的序号是负的；并且用负数的绝对值作为这个集合中所含结点的个数。例如，如果parent[7]=-4，说明７号结点就是它所在集合的根结点，这个集合有四个元素。初始时结点的parent值为－１（每个结点都是根结点，只包含它自己一个元素）。

　　实现并查集数据结构主要有2个函数。

 import java.util.HashSet;
 import java.util.Set;

 public class UnionFind {

     public static UFNode find(UFNode x) {
         UFNode p = x;
         Set<UFNode> path = new HashSet<UFNode>();
         // 记录向上追溯的路径上的点
         while (p.parent != null) {
             path.add(p);
             p = p.parent;
         }
         // 这些点的parent全部指向这个集的代表
         for (UFNode ppp : path) {
             ppp.parent = p;
         }
         // root
         return p;

     }

     public static void union(UFNode x, UFNode y) {
         find(y).parent = find(x);
     }

     public static class UFNode {
         UFNode parent;
     }
 }

　　最后贴出边集的代码

 /**
  * 边 的封装
  * 边集可以用来表示图
  */
 public class Edge<T> implements Comparable<Edge>  {
     private T start;
       private T end;
       private int distance;

       public Edge(T start, T end, int distance) {
         this.start = start;
         this.end = end;
         this.distance = distance;
       }

       public T getStart() {
         return start;
       }

       public void setStart(T start) {
         this.start = start;
       }

       public T getEnd() {
         return end;
       }

       public void setEnd(T end) {
         this.end = end;
       }

       public int getDistance() {
         return distance;
       }

       public void setDistance(int distance) {
         this.distance = distance;
       }

       @Override
       public String toString() {
         return start + "->" + end + ":" + distance;
       }

       @Override
       public int compareTo(Edge obj) {
         int targetDis = obj.getDistance();
         return distance > targetDis ? 1 : (distance == targetDis ? 0 : -1);
       }
 }

　　最后运行Kruskal类的结果为：

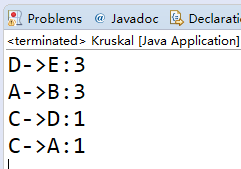
　　例题：POJ- 1287，蓝桥杯-城市建设。