exgcd学习笔记

扩展欧几里得算法是当已知a和b时，求得一组x和y使得

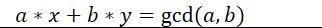
首先，根据数论中的相关定理，解一定存在        //留坑待填

之后我们可以推一推式子

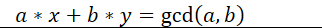
将a替换掉

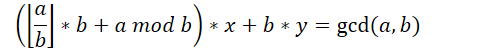
展开括号

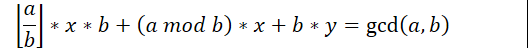
提出b，合并

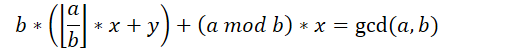
且

　　

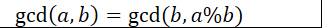
设

　　

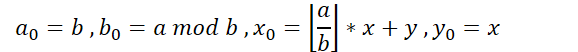
现在已经将原来的式子转化为一个小一点的问题了

当  b = 0 时，则有 x = 1 , y = 0

之后递归回去就可以求得最终的x和y了

整理上面的和可以得到：

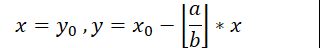
之后代码就很好写了

int exgcd(int a,int b,int &x,int &y){
	if(b==0){
		x=1;
		y=0;
		return a;
	}
	int res,tmp;
	res=exgcd(b,a%b,x,y);
	tmp=x;
	x=y;
	y=tmp-a/b*y;
	return res;
}

---

upd：

　　拿一道例题来说事 ： 青蛙的约会