DFA确定有限状态自动机

DFA

在计算理论中，确定有限状态自动机或确定有限自动机（英语：deterministic finite automaton, DFA）是一个能实现状态转移的自动机。对于一个给定的属于该自动机的状态和一个属于该自动机字母表Σ的字符，它都能根据事先给定的转移函数转移到下一个状态（这个状态可以是先前那个状态）。

可以通过建立状态机来解决问题。

每次输入都会引起状态的改变或者不变。再次输入一个值，状态又会改变。

我们把所有状态罗列出来，每次输入都改变他的状态。如果最后的状态是合法的，那么证明这个输入符合条件。

例题

一个仅有ab的字符串，要求b需要成对出现，否则不合法。就是(a|bb)*正则的匹配。我们可以用dfa来做这个题。

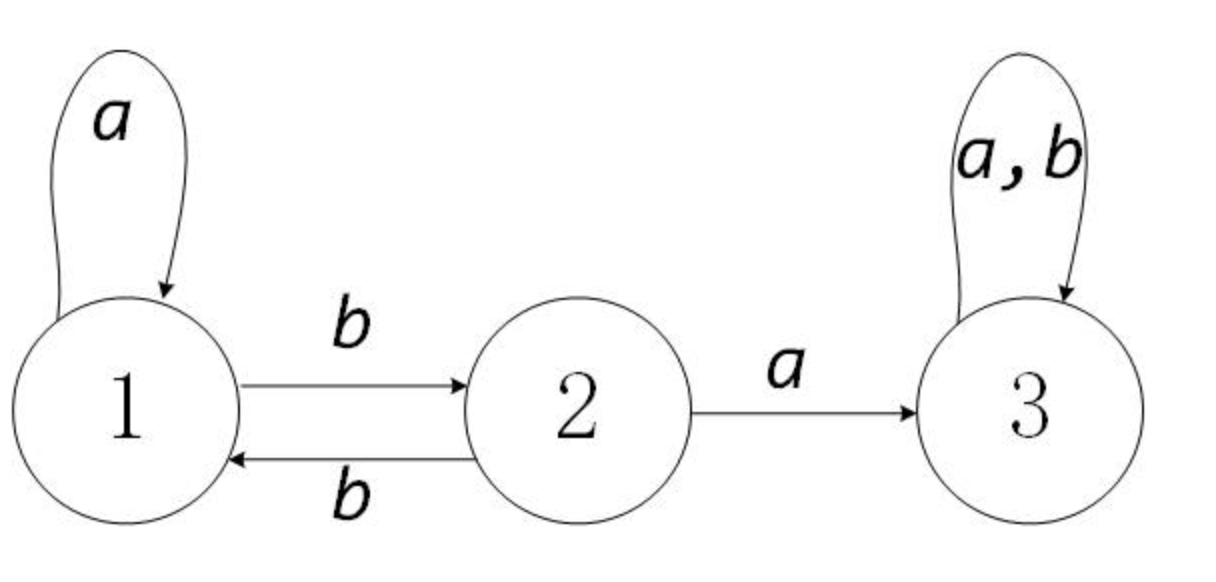
我们可以通过要求生成这样一个自动机：

字符串一共有3种状态，分别是没有b的状态或者b合法的状态，“a”，只有一个b的临时状态“ab”，b不匹配的“aba”状态。

1. 没有输入的时候处于状态1，当输入一个a的时候还是处于状态1。
2. 当输入一个b的时候处于状态2。变成“xxxxab”
3. 当状态2再输入一个b，这是变成“abb”合法，又回到状态1.
4. 当状态2再输入一个a，这时变成了“aba”不合法状态，成为状态3
5. 状态3无论输入什么都是不合法的，都是状态3。

这时候可以用一个数组表示这个状态机：

    a   b
1  1   2
2  3   1
3  3   3

把ab也用1，2表示。

 var runs = function(str) {
      var dfa = [
          [],
          [1, 2],
          [3, 1],
          [3, 3],
      ];
      var state = 1;
      for (var i = 0; i < str.length; i++) {
          if(str[i] == 'a'){
            state = dfa[state][0];
          } else if(str[i] == "b") {
            state = dfa[state][1];
          }

          if(state === 3) {
            return state;
          }
      }
      return state
    };
    console.log(runs("abbaaa"))

当最后一个输入结束之后，看一下最后的状态是处于状态几，通过自动机可以发现，只有在状态1的时候是合法的。所以我只需要判断state === 1.