B+树在磁盘存储中的应用

欢迎探讨，如有错误敬请指正

如需转载，请注明出处 http://www.cnblogs.com/nullzx/

---

我们首先提一个问题， B+树比平衡二叉树在索引数据方面要快么？

大多数人可能认为肯定还是B+树快，毕竟存储同样多的数据，100阶的B+树肯定比平衡二叉树的高度要低的多。但是别忘了B树在一个结点可能需要比较很多次才能找到下一层的结点，但是平衡二叉树只要比较一次就可以向下走一层。所以综合起来，其实两者索引的速度几乎（甚至说就是）是一样的。最简单的道理，一颗4阶B树就是一颗红黑树，比较的次数完全一样（如果不明白这个道理，请参考我关于红黑树的三篇技术博客）。那么我们为什么还要使用B+树呢？这是因为上面说索引速度相当的前提是两者的数据结构都位于内存中，当我们要在磁盘上索引一个记录时，将磁盘中的数据传输到内存中才是花费时间的大头，而在内存中的索引过程所花的时间基本是可以忽略不计的。在磁盘中以B+树的形式组织数据就有着天然的优势。要解释这个道理，我们必须先强调一个概念，主存和磁盘之间的数据交换不是以字节为单位的，而是以n个扇区为单位的（一个扇区有512字节），通常是4KB（8个扇区），8KB（16个扇区），16KB，……64KB为单位的。假设，我们现在选择4KB作为内存和磁盘之间的传输单位，那么我们在设计B+树的时候，不论是索引结点还是叶子结点都使用4KB作为结点的大小。我们这时不妨再假设一个记录的大小是1KB，那么一个叶子结点可以存4个记录。而对于索引结点（大小也是4KB），由于只需要存key值和相应的指针，所以一个索引结点可能可以存储100~150个分支，我们不妨就取100吧。当然这和上面第2节和第三节中的情况不太一样，因为现在索引结点的阶数是100，而叶子结点的阶数是4，两者并不一致，但这并没有什么问题。

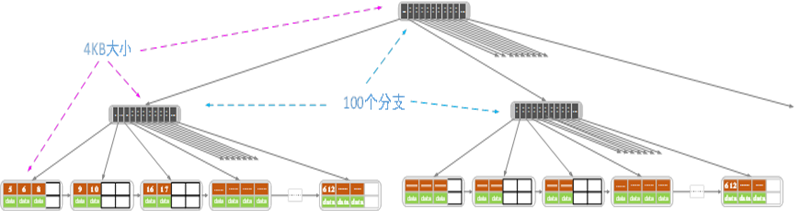
我们考虑如上图所示的B+树，下面的B+树有三层，两层是索引结点，最后一层是叶子结点。那么这个三层的B+树最多可以存400万个记录。如果这个B+树存储到硬盘中，我们怎么根据记录的key找到对应的记录呢？首先我们要读取这个B+树的根结点到内存（花费一个IO的时间）然后在内存中进行索引，然后根据key找到对应的分支，再将这个分支所指向的第二层索引结点读取到内存中（花费第二个IO时间）然后在内存中进行索引，同样根据key找到对应的分支，而这个分支指向的就是叶子结点，我们最后将这个叶子结点读取到内存中（花费的第三个IO时间）判断是否存在这个记录。这样我们只需要通过三次IO时间就从400万个记录中找到了对应的key记录，可以说是非常快了。快速的原因是，索引结点中不存数据，只存键和指针，所以一个索引结点就可以存储大量的分支，而一个索引结点只需要一次IO即可读取到内存中。

我们现在再考虑一个问题，当记录的大小可变时，叶子结点中记录该如何存储？

这个时候有两种极限情况。

1）假设叶子结点的阶数仍然为4，但每个记录仅仅有100个字节，显然当叶子结点中存满4个记录后，叶子结点中仍然有大量的剩余空间。这个时候我们能不能直接向该叶子结点中插入数据，而不必分裂这个叶子结点（分裂指在磁盘中的分裂）？答案是可以，有人一定会说，这不就违反B+树的定义了么？的确违反了，但是B+树之所以定义阶数的目的是为了平衡（或者说增强）每一个分支的索引效率，不过这个优点仅当整个B+树都位于内存时才能体现出来。当B+树存储在磁盘中的情况时，IO效率才是第一要考虑的因素。CPU在某个结点内部多比较几次或少比较几次和IO花费的时间相比就不值得一提了。而不分裂反而能提升B+树的IO效率，因为分裂需要更多的IO次数。综合起来了说就是，文件系统及数据库中的B+树是不考虑阶数这一个概念的，结点（即包括叶子结点，也包括索引结点）中仅遵行一个规则，如果剩余空间够大那么就存入数据，如果剩余空间不够，只能分裂后再存入。

2）如果某条记录太大，即使叶子结点中还剩余一多半的空间但仍然存不下怎么办？这个时候MySql称之为行溢出，简单的解决方式就是把记录存储在溢出页（磁盘的其它空闲地方）中，然后叶子结点中存储的是这个记录的指针。

补充：如果按照key值的大小顺序插入，按照B+树定义的方式进行分裂时，每个叶子结点的存储效率只有50%，为了解决这个问题，我们可以采取这样的分裂方式：原叶子结点中的数据不动，创建一个新的空叶子结点，记录插入到新叶子节点中。这样磁盘的插入效率就很高，而且每个叶子结点的利用率也很高。但这种分裂方式仅仅对按key的大小将记录顺序插入才有效，随机插入条件反而不如50%分裂的方式。

参考内容

[1] B+树介绍

[2] 从MySQL Bug#67718浅谈B+树索引的分裂优化

[3] B+树的几点总结