平衡树学习笔记（6）-------RBT

RBT

上一篇：平衡树学习笔记（5）-------SBT

RBT是。。。是一棵恐怖的树

有多恐怖？

平衡树中最快的♂

不到200ms的优势，连权值线段树都无法匹敌

但是，通过大量百度，发现RBT的代码都是从STL扒的qwq

蒟蒻根本无法研究透彻

关键时候，崔大钊(<-----数据结构巨佬)使用了终极武器花_Q帮助了我(雾

硬生生把左旋右旋压在一起，800多行-->100多行，使我更加透彻QAQ

感激不尽(^▽)

不废话了qwq

RBT，中文名红黑树，即Red-Black-Tree

是个巨佬级别的数据结构

它为每个点规定了颜色（不是红就是黑）

下面说它的几个性质

\(\color{#3399ff}{1、每个节点有且只有两种颜色：黑||红}\)

\(\color{#3399ff}{2、根为黑色}\)

\(\color{#3399ff}{3、叶子节点为黑色。注：叶子节点是额外的空节点}\)

\(\color{#3399ff}{4、如果某节点是红色的，那么TA的左右儿子必须是黑色的}\)

\(\color{#3399ff}{5、从每个节点出发，到它子树内的叶子节点所经过的黑节点的个数相同，我们把这个黑节点的个数称为黑高度}\)

可以仔细思(tou)考(che)一下，不难发现，RBT保证平衡的方法

由于性质5，可以发现每个点向下的几条链中，最长链不会超过最短链的二倍

这是为什么呢

最长链，即为红黑交替，（保证性质4、5）

最短链，就是全黑了

那么黑高度相同，长链自然不会超过短链的二倍（其实这里不太严谨，应该是二倍+1，反正大概就是这样的）

举几个RBT栗子，来更好的认识RBT

违反性质1

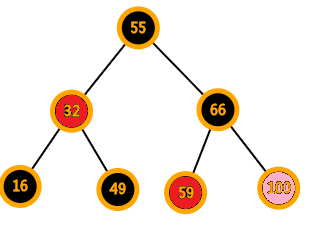
违反性质2

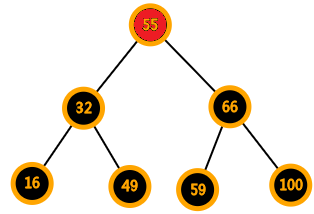
违反性质4、5

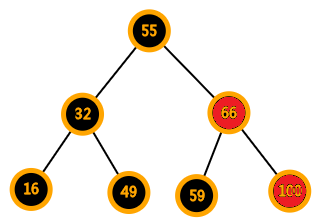
正版红黑树

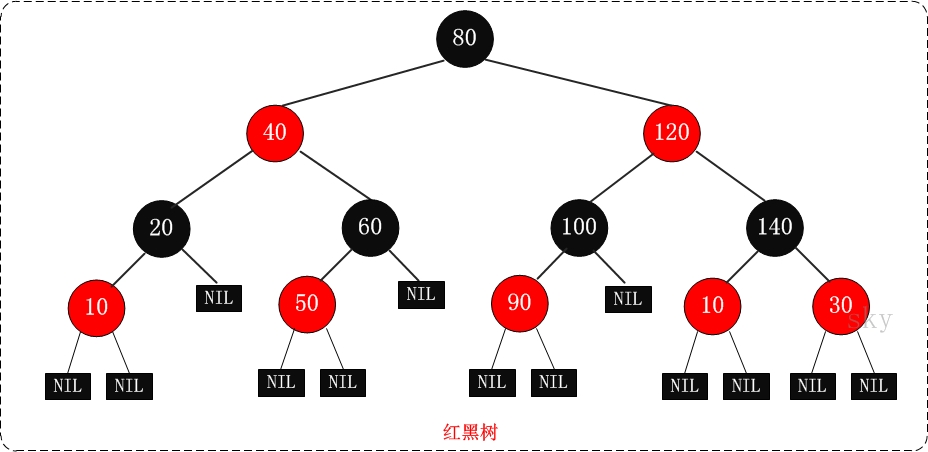
下面进入正题吧

\(\color{#9900ff}{定义}\)

enum Color{RED,BLACK};
struct node
{
    //每个节点维护父亲，孩纸，颜色，大小，以及权值
    node *fa,*ch[2];
    int siz,val;
    Color col;
    //siz维护要判空！
    void upd()
    {
        siz=1;
        if(ch[0]) siz+=ch[0]->siz;
        if(ch[1]) siz+=ch[1]->siz;
    }
    //下面的根Splay差不多
    bool isr() { return fa->ch[1]==this;}
    int rk()   { return ch[0]? ch[0]->siz+1:1;}
};

RED,BLACK相当于两个变量，0/1，作为节点的颜色

前方高能！！

3

2

1

\(\color{#9900ff}{基本操作}\)

1、双红修正

这。。。名字居然是中文的。。。

因为这个操作不用单独写一个函数！

为什么呢？ 因为这个操作只有在插入才会用到（毕竟插入会改变形态）

那删除呢？他不也会改变形态吗？

别急，那是操作二

根据操作的名字，大概脑补一下发生了什么qwq

首先，根据性质1，插入的节点必须要有颜色

那么我们到底给它什么颜色呢

如果给黑色的话， 很显然这条链的黑高度+1，那么整条链上所有的点都会受影响

但是如果我们插入红节点，首先性质5是一定不会因此而改变的

违反的性质越少，我们需要改变的也就越少，这也是我们所期望的，所以我们插入的点为红节点

但是我们要判断性质4的问题

这就是双红修正，解决的是插入之后违反性质4的问题

我们要分情况讨论

首先，如果插入点的父亲是黑节点，RBT性质显然是满足的，我们也不用做任何修改，直接return就行了qwq（这样绝对快（O（1）））

但是，如果插入点的父亲是红节点，怎么办呢

这时候就要双红修正了

注：以下，t为要恢复的节点，o为t的父亲，z为o的父亲，b为o的兄弟

有些图单独并不是红黑树，只是为了方便理解，部分子树没画

\(\color{#FF0099}{Case：1}\)

插入点父亲的兄弟b为红色

即下面左图所示

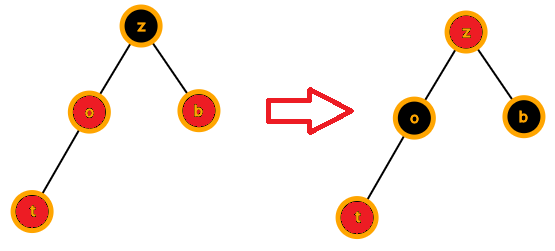
这时候我们要让B和C变黑，A变红（因为原树一定是满足性质的，所以A一定是黑色）

这是不难发现，子树A的缺陷没了！！！真的没了！！！

而且黑高度还没有变！！！

别高兴的太早

A变成了红色，它父亲要是红色咋办呢？？

所以，这就成为了一个子问题，出问题的节点自然转变成了A，继续算法即可

那总得有个边界吧。

没错，就是到根节点

直接让根变黑可以满足所有性质

\(\color{#FF0099}{Case：2}\)

插入点父亲的兄弟b为黑色且z,o,t三点不是一条直线

我们需要把它们弄成一条直线，所以转o

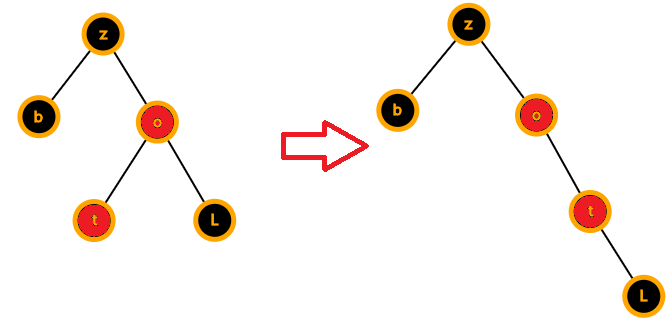
左图为原来的情况，右图为转完后的情况，因为o是t的父亲，转完后，swap（o，t）

这样，问题转化为了第三种情况

\(\color{#FF0099}{Case：3}\)

插入点父亲的兄弟b为黑色且z,o,t三点是一条直线

这是后就好办了，现在是满足性质5的

我们让z变红，o变黑，会发生什么？

左面的黑高度-1

那么我们需要让左边共享右边的o

直接把o转上来就行了

而且因为o是黑的，所以一切都结束了qwq

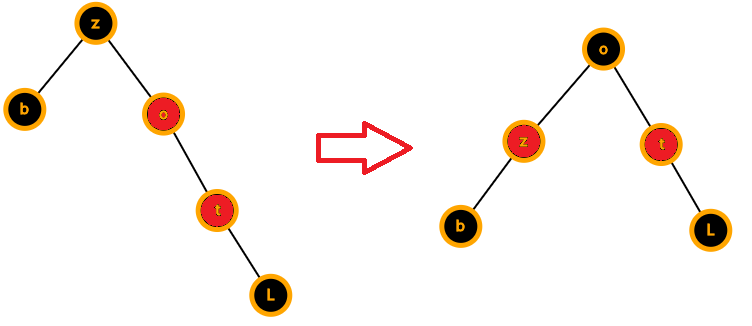
双红修正完成！

void ins(int val)
{
    //根为空特判，直接开新节点，一定注意根是黑的
    if(root==NULL) {root=newnode(val);root->col=BLACK;return;}
    //否则就开始插入了
    nod o=root,t=newnode(val),z;
    int k;
    while(o->siz++,o->ch[k=(val>=o->val)]) o=o->ch[k];
    //暴力找插入位置，沿途siz++
    t->fa=o,o->ch[k]=t,o->upd();
    //该维护的维护好，t是插入节点，也是可能要维护的第一个问题节点
    //情况1的转化子问题过程，只要问题节点不是根（是根就根据情况1直接结束了）
    //并且有问题（就是违反了性质4）
    //那么就一直进行双红修正
    while((o=t->fa)&&(o->col==RED))
    {
        //z是o的父亲
        z=o->fa;
        //判断儿子方向
        int k1=o->isr(),k2=t->isr();
        //b是兄弟
        nod b=z->ch[!k1];
        //先判b是否为空，然后如果是红色，那么就是情况1了
        if(b&&b->col==RED)
        {
            //缺陷上传到z，当前问题节点为t=z，继续算法
            b->col=o->col=BLACK;
            z->col=RED,t=z;
            continue;
        }
        //否则就是情况2或3
        //如果是情况2，就需要旋转，把o转下去，别忘交换ot（上面说了）
        if(k1^k2) rot(o,k1),std::swap(o,t);
        //剩下的就是单纯的情况3了
        //把z变红，o变黑，然后z转下去（即o转上来）
        o->col=BLACK,z->col=RED;
        rot(z,!k1);
    }
    //根的颜色为黑！！！！
    root->col=BLACK;
}

上面一定要好好理解！

2、双黑修正

这是红黑树最cd的一段

首先先说删的方法，之后再说维护的问题

我们没有splay的旋转，也没有Treap的merge

那怎么删除？

想象一下，如果要删的点至少一个儿子为空，那么直接把另一个儿子接上来不就行了？

所以如果当前点两个儿子都有，我们可以找它的后继

因为是后继，所以它至少是没有左孩子的，也就符合刚刚的条件

于是把它后继的值给当前点，然后问题就转化为删它的后继了

这就是删除的方式

然后我们考虑维护性质

因为我们不能保证删的点是红节点啊

所以恶心的性质5就可能出锅

如果删的节点使红节点，那就简单了，因为不会影响任何红黑树的性质，算法直接结束

算是O(1)删除了吧qwq

要是删的是黑节点。。。。就有问题了。。。。

下面讨论删的是黑节点的情况

既然删了一个黑节点，显然它所在链黑高度--

而第5性质恰恰是不好维护的

我们不妨转化一下

当我们将黑节点x删除时，强制将其的黑色压到齐孩子节点上

而且孩子节点原来的颜色依然存在

这样就违反了性质1，但是性质5却成立了

那么现在就想办法去掉那一层颜色

\(\color{#FF0099}{Case：1}\)

x一层红，一层黑

显然直接去掉那一层红是不影响性质的qwq

\(\color{#FF0099}{Case：2.1}\)

x是黑+黑且为根节点

这时我们去掉一层黑，让所有黑高度-1，依然不会违反性质，成立！

\(\color{#FF0099}{Case：2.2.0}\)

这个麻烦了

x是黑+黑且不是根

我们将其分为了4种情况

\(\color{#FF0099}{Case：2.2.1}\)

x的兄弟为红，那么显然x的父亲，x兄弟的儿子一定都是黑的（性质4）

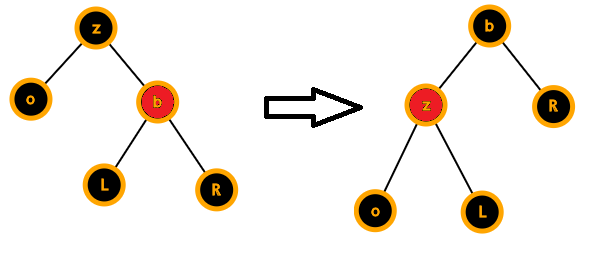
我们把z染红，b染黑，然后把b转上来

这时候情况转化为了下面三种情况之一

当然不要忘了b是o的兄弟，旋转之后要把更新b指向的节点L

\(\color{#FF0099}{Case：2.2.2}\)

兄弟为黑色，兄弟的两个儿子全是黑色

这时可以把那一重黑色上移到z节点上

于是b要改变成红色，因为b的路径上多了一个黑高度

对于在z上的那个黑色，此时显然z就是违反性质1的节点，我们下次只需让o=z，继续子问题即可

而此时，如果z是红色，那就是红+黑问题了啊，就直接结束了qwq

上图的绿色代表可以是任意颜色（红/黑）

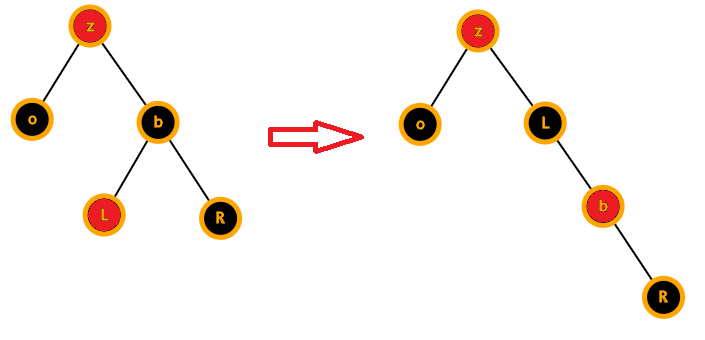
\(\color{#FF0099}{Case：2.2.3}\)

兄弟为黑，兄弟的d儿子为红色，!d儿子为黑色

注：d是o是父亲的哪个儿子，也就是说o是父亲的哪个儿子，b的哪个儿子就是红色，另一个就是黑色

这时我们把b染红，把d孩子染黑，然后把d孩子转上去，就转化为了情况4

\(\color{#FF0099}{Case：2.2.4}\)

兄弟为黑，兄弟的!d儿子为红色

这时我们把b转上来，然后可以发现，原来的z和原来的b的!d孩子都是红色，这是一个机会！！

我们可以做一个神奇的操作来去掉o上的黑色！

我们把那两个红色的点变黑，上面那个黑点变红，即黑色下放到两个子树

用下图的左边与右边对比一下，左子树多了一个黑！！！

这时候，我们去掉一个黑，也就是那一重黑，不就行了？

为了方便，这是可以直接把o=root，下次循环就出去了

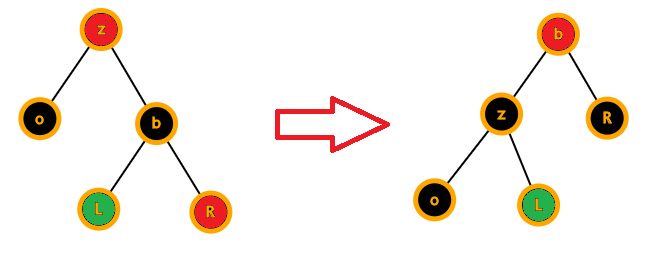
上面非常重要，是红黑树的精髓！

这么cd的东西，代码肯定不会短

记得参考的代码好像有200行。。。

//o是双黑节点，z是o的父亲，因为o可能是NULL，所以防止判断左右儿子的时候RE，传进了一个父亲参数
void fix(nod o,nod z)
{
    //兄弟节点b
    nod b;
    //只要o是黑的（不管空不空，它是双黑的qwq）并且o不是根
    while((!o||o->col==BLACK)&&o!=root)
    {
        //k就是儿子的方向
        bool k=z->ch[1]==o;
        //确认兄弟节点
        b=z->ch[!k];
        //双黑情况1，兄弟为红，该换色的换色，然后旋转，别忘了更新b！这样情况转为2/3/4
        if(b->col==RED) b->col=BLACK,z->col=RED,rot(z,k),b=z->ch[!k];
        //如果兄弟的儿子全黑，则为双黑情况2，染红b（黑色上移），双黑节点变为z，所以o=z
        //这时候如果o是红的（就是原来z是红的，就是黑+红的情况，直接变黑就行，在while中结束，下面染黑）
        if((!b->ch[0]||b->ch[0]->col==BLACK)&&(!b->ch[1]||b->ch[1]->col==BLACK)) b->col=RED,o=z,z=o->fa;
        else
        {
            //这就是说明兄弟有红儿子了
            //如果!k是黑，显然k就是红了，这就是双黑情况3
            if(!b->ch[!k]||b->ch[!k]->col==BLACK) b->ch[k]->col=BLACK,b->col=RED,rot(b,!k),b=z->ch[!k];
            //情况3会转化为情况4，这是直接break，因为o=root（其实不写break也一样）
            b->col=z->col,z->col=BLACK,b->ch[!k]->col=BLACK,rot(z,k);
            o=root;
            break;
        }
    }
    //只要不空就染黑（根据上面所述）
    if(o) o->col=BLACK;
}
//找到权为k的点
nod sch(const int &k)
{
    nod o=root;
    while(o&&o->val!=k) o=o->ch[k>=o->val];
    return o;
}
//删除权为val的点
void del(const int &val)
{
    nod o=root,z,f,p,g;
    Color tmp;
    //树中都没这个点，还删个毛线，返回就行了
    if(sch(val)==NULL) return;
    //否则就往下找，沿途siz--（因为要删一个点）
    while(o&&o->val!=val) o->siz--,o=o->ch[val>=o->val];
    o->siz--;
    //如果它两个孩子都有，那么根据前面所说，我们要删它后继
    if(o->ch[0]&&o->ch[1])
    {
        //p是它后继，z是它父亲，
        p=o->ch[1],z=o->fa;
        //让p找到它父亲，显然p没有左孩子（右孩子不一定有）
        while(p->ch[0]) p->siz--,p=p->ch[0];
        //认儿子，注意判根（把o删了，p接上）
        if(z) z->ch[o->isr()]=p;
        else root=p;
        //删p，要把它的孩子接上，g就是那个孩子（可能为空）
        //现在要把g接在f上
        g=p->ch[1],f=p->fa,tmp=p->col;
        //特盘直接相连的情况
        if(f==o) f=p;
        else
        {
            //认父亲，认儿子
            if(g) g->fa=f;
            f->ch[0]=g,p->ch[1]=o->ch[1],o->ch[1]->fa=p;
            //更新siz
            f->upd();
        }
        //这是把原来o的东西全给p（相当于让p取代了o，而原来的p（后继）也因g与f相接而不复存在了）
        p->siz=o->siz,p->fa=z,p->col=o->col,p->ch[0]=o->ch[0],o->ch[0]->fa=p;
        //如果是黑色在进入双黑修正
        if(tmp==BLACK) fix(g,f);
        //删掉o就行了
        st[top++]=o;
    }
    else
    {
        //o本身有空儿子，就让p的o的不空的儿子来接上z
        p=o->ch[o->ch[1]!=NULL];
        z=o->fa,tmp=o->col;
        //pz父子相认（由爷孙变成父子）
        if(p) p->fa=z;
        if(z) z->ch[o->isr()]=p;
        else root=p;
        //如果原色为黑，则因为又来了个黑，就双黑修正
        if(tmp==BLACK) fix(p,z);
        //删o
        st[top++]=o;
    }
}

\(\color{#9900ff}{其它操作}\)

插入删除上面都说了，就不解释了

由于其它的操作跟基本操作没关系了，所以近乎暴力查找qwq

int nxt(int val)
{
    int ans=inf;
    nod t=root;
    while(t)
    {
        if(val>=t->val)t=t->ch[1];
        else ans=std::min(ans,t->val),t=t->ch[0];
    }
    return ans;
}
int pre(int val)
{
    int ans=-inf;
    nod t=root;
    while(t)
    {
        if(val<=t->val)t=t->ch[0];
        else ans=std::max(ans,t->val),t=t->ch[1];
    }
    return ans;
}
int rnk(int x)
{
    int ans=1;
    nod o=root;
    while(o)
    {
        if(o->val<x) ans+=o->rk(),o=o->ch[1];
        else o=o->ch[0];
    }
    return ans;
}
int kth(int k)
{
    nod o=root;
    int num;
    while((num=o->rk())!=k)
    {
        if(num<k)k-=num,o=o->ch[1];
        else o=o->ch[0];
    }
    return o->val;
}

这就是神奇的红黑树qwq

放下完整代码（网上找了好久，都是从STL等地扒的，研究了好久）

#include<cstdio>
#include<queue>
#include<vector>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cctype>
#include<cmath>
#define _ 0
#define LL long long
#define Space putchar(' ')
#define Enter putchar('\n')
#define fuu(x,y,z) for(int x=(y),x##end=z;x<=x##end;x++)
#define fu(x,y,z)  for(int x=(y),x##end=z;x<x##end;x++)
#define fdd(x,y,z) for(int x=(y),x##end=z;x>=x##end;x--)
#define fd(x,y,z)  for(int x=(y),x##end=z;x>x##end;x--)
#define mem(x,y)   memset(x,y,sizeof(x))
#ifndef olinr
inline char getc()
{
    static char buf[100001],*p1=buf,*p2=buf;
    return (p1==p2)&&(p2=(p1=buf)+fread(buf,1,100001,stdin),p1==p2)? EOF:*p1++;
}
#else
#define getc() getchar()
#endif
inline int in()
{
    int f=1,x=0; char ch;
    while(!isdigit(ch=getc()))(ch=='-')&&(f=-f);
    while(isdigit(ch)) x=x*10+(ch^48),ch=getc();
    return x*f;
}
enum Color{RED,BLACK};
struct node
{
    node *fa,*ch[2];
    int siz,val;
    Color col;
    void upd()
    {
        siz=1;
        if(ch[0]) siz+=ch[0]->siz;
        if(ch[1]) siz+=ch[1]->siz;
    }
    bool isr() { return fa->ch[1]==this;}
    int rk()   { return ch[0]? ch[0]->siz+1:1;}
};
typedef node* nod;
nod st[105050],root;
int top;
const int inf=0x7fffffff;
nod newnode(int val)
{
    static node s[105050],*tail=s;
    nod o=top? st[--top]:tail++;
    o->fa=o->ch[0]=o->ch[1]=NULL;
    o->siz=1,o->val=val,o->col=RED;
    return o;
}
void rot(nod x,bool k)
{
    nod y=x->ch[!k],z=x->fa;
    x->ch[!k]=y->ch[k];
    if(y->ch[k]) y->ch[k]->fa=x;
    y->fa=z;
    if(z) z->ch[x->isr()]=y;
    else root=y;
    y->ch[k]=x,x->fa=y;
    x->upd(),y->upd();
}
void ins(int val)
{
    if(root==NULL) {root=newnode(val);root->col=BLACK;return;}
    nod o=root,t=newnode(val),z;
    int k;
    while(o->siz++,o->ch[k=(val>=o->val)]) o=o->ch[k];
    t->fa=o,o->ch[k]=t,o->upd();
    while((o=t->fa)&&(o->col==RED))
    {
        z=o->fa;
        int k1=o->isr(),k2=t->isr();
        nod b=z->ch[!k1];
        if(b&&b->col==RED)
        {
            b->col=o->col=BLACK;
            z->col=RED,t=z;
            continue;
        }
        if(k1^k2) rot(o,k1),std::swap(o,t);
        o->col=BLACK,z->col=RED;
        rot(z,!k1);
    }
    root->col=BLACK;
}
nod sch(const int &k)
{
    nod o=root;
    while(o&&o->val!=k) o=o->ch[k>=o->val];
    return o;
}
void fix(nod o,nod z)
{
    nod b;
    while((!o||o->col==BLACK)&&o!=root)
    {
        bool k=z->ch[1]==o;
        b=z->ch[!k];
        if(b->col==RED) b->col=BLACK,z->col=RED,rot(z,k),b=z->ch[!k];
        if((!b->ch[0]||b->ch[0]->col==BLACK)&&(!b->ch[1]||b->ch[1]->col==BLACK)) b->col=RED,o=z,z=o->fa;
        else
        {
            if(!b->ch[!k]||b->ch[!k]->col==BLACK) b->ch[k]->col=BLACK,b->col=RED,rot(b,!k),b=z->ch[!k];
            b->col=z->col,z->col=BLACK,b->ch[!k]->col=BLACK,rot(z,k);
            o=root;
            break;
        }
    }
    if(o) o->col=BLACK;
}
void del(const int &val)
{
    nod o=root,z,f,p,g;
    Color tmp;
    if(sch(val)==NULL) return;
    while(o&&o->val!=val) o->siz--,o=o->ch[val>=o->val];
    o->siz--;
    if(o->ch[0]&&o->ch[1])
    {
        p=o->ch[1],z=o->fa;
        while(p->ch[0]) p->siz--,p=p->ch[0];
        if(z) z->ch[o->isr()]=p;
        else root=p;
        g=p->ch[1],f=p->fa,tmp=p->col;
        if(f==o) f=p;
        else
        {
            if(g) g->fa=f;
            f->ch[0]=g,p->ch[1]=o->ch[1],o->ch[1]->fa=p;
            f->upd();
        }
        p->siz=o->siz,p->fa=z,p->col=o->col,p->ch[0]=o->ch[0],o->ch[0]->fa=p;
        if(tmp==BLACK) fix(g,f);
        st[top++]=o;
    }
    else
    {
        p=o->ch[o->ch[1]!=NULL];
        z=o->fa,tmp=o->col;
        if(p) p->fa=z;
        if(z) z->ch[o->isr()]=p;
        else root=p;
        if(tmp==BLACK) fix(p,z);
        st[top++]=o;
    }
}
int nxt(int val)
{
    int ans=inf;
    nod t=root;
    while(t)
    {
        if(val>=t->val)t=t->ch[1];
        else ans=std::min(ans,t->val),t=t->ch[0];
    }
    return ans;
}
int pre(int val)
{
    int ans=-inf;
    nod t=root;
    while(t)
    {
        if(val<=t->val)t=t->ch[0];
        else ans=std::max(ans,t->val),t=t->ch[1];
    }
    return ans;
}
int rnk(int x)
{
    int ans=1;
    nod o=root;
    while(o)
    {
        if(o->val<x) ans+=o->rk(),o=o->ch[1];
        else o=o->ch[0];
    }
    return ans;
}
int kth(int k)
{
    nod o=root;
    int num;
    while((num=o->rk())!=k)
    {
        if(num<k)k-=num,o=o->ch[1];
        else o=o->ch[0];
    }
    return o->val;
}
int main()
{
    int n=in();
    while(n--)
    {
        int op=in();
        if(op==1)ins(in());
        if(op==2)del(in());
        if(op==3)printf("%d\n",rnk(in()));
        if(op==4)printf("%d\n",kth(in()));
        if(op==5)printf("%d\n",pre(in()));
        if(op==6)printf("%d\n",nxt(in()));
    }
    return 0;
}