【bzoj4378】[POI2015]Logistyka 离散化+树状数组

题目描述

维护一个长度为n的序列，一开始都是0，支持以下两种操作：
1.U k a 将序列中第k个数修改为a。
2.Z c s 在这个序列上，每次选出c个正数，并将它们都减去1，询问能否进行s次操作。
每次询问独立，即每次询问不会对序列进行修改。

输入

第一行包含两个正整数n,m(1<=n,m<=1000000)，分别表示序列长度和操作次数。
接下来m行为m个操作，其中1<=k,c<=n，0<=a<=10^9，1<=s<=10^9。

输出

包含若干行，对于每个Z询问，若可行，输出TAK，否则输出NIE。

样例输入

3 8
U 1 5
U 2 7
Z 2 6
U 3 1
Z 2 6
U 2 2
Z 2 6
Z 2 1

样例输出

NIE
TAK
NIE
TAK

---

题解

离散化+树状数组

刚开始看错题意了，以为是在某个选定的区间中查询，想了一大堆离线算法发现还是搞不出来，然后才注意到是查询整个序列。。

每次选出c个正数，并将它们都减去1，能进行s次操作的充分必要条件是：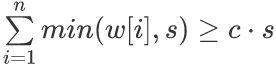

因为每个数最多只能被选min(w[i],s)次。

这个式子可以用树状数组快速求出，方法为离散化后求出小于等于s的数的和以及个数，再用n减去个数即为大于s的个数。这里使用了2个树状数组。

结构体能够大大减少代码量~

#include <cstdio>
#include <algorithm>
#define N 1000010
using namespace std;
typedef long long ll;
int m , x[N] , opt[N] , top;
ll y[N] , v[N] , w[N];
char str[5];
struct data
{
	ll f[N];
	void update(int x , int a)
	{
		int i;
		for(i = x ; i <= m + 1 ; i += i & -i) f[i] += a;
	}
	ll query(int x)
	{
		int i;
		ll ans = 0;
		for(i = x ; i ; i -= i & -i) ans += f[i];
		return ans;
	}
}num , sum;
int main()
{
	int n , i , tmp;
	scanf("%d%d" , &n , &m);
	v[0] = 1;
	for(i = 1 ; i <= m ; i ++ ) scanf("%s%d%lld" , str , &x[i] , &y[i]) , y[i] ++ , v[i] = y[i] , opt[i] = (str[0] == 'Z');
	sort(v , v + m + 1);
	for(i = 1 ; i <= n ; i ++ ) num.update(1 , 1) , w[i] = 1;
	for(i = 1 ; i <= m ; i ++ )
	{
		tmp = lower_bound(v , v + m + 1 , y[i]) - v + 1;
		if(opt[i]) printf("%s\n" , (n - num.query(tmp)) * (y[i] - 1) + sum.query(tmp) >= x[i] * (y[i] - 1) ? "TAK" : "NIE");
		else num.update(lower_bound(v , v + m + 1 , w[x[i]]) - v + 1 , -1) , sum.update(lower_bound(v , v + m + 1 , w[x[i]]) - v + 1 , 1 - w[x[i]]) , num.update(tmp , 1) , sum.update(tmp , y[i] - 1) , w[x[i]] = y[i];
	}
	return 0;
}