为什么L1稀疏，L2平滑？

使用机器学习方法解决实际问题时，我们通常要用L1或L2范数做正则化（regularization），从而限制权值大小，减少过拟合风险。特别是在使用梯度下降来做目标函数优化时，很常见的说法是,  L1正则化产生稀疏的权值, L2正则化产生平滑的权值。为什么会这样？这里面的本质原因是什么呢？下面我们从两个角度来解释这个问题。

角度一：数学公式

这个角度从权值的更新公式来看权值的收敛结果。

首先来看看L1和L2的梯度(导数的反方向）：

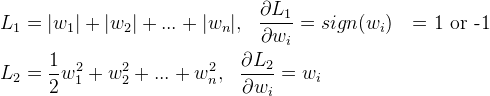
所以(不失一般性，我们假定：wi等于不为0的某个正的浮点数，学习速率η 为0.5)：

L1的权值更新公式为w_i = w_i - η * 1  = w_i - 0.5 * 1，也就是说权值每次更新都固定减少一个特定的值(比如0.5)，那么经过若干次迭代之后，权值就有可能减少到0。

L2的权值更新公式为w_i = w_i - η * w_i = w_i - 0.5 * w_i，也就是说权值每次都等于上一次的1/2，那么，虽然权值不断变小，但是因为每次都等于上一次的一半，所以很快会收敛到较小的值但不为0。

下面的图很直观的说明了这个变化趋势：

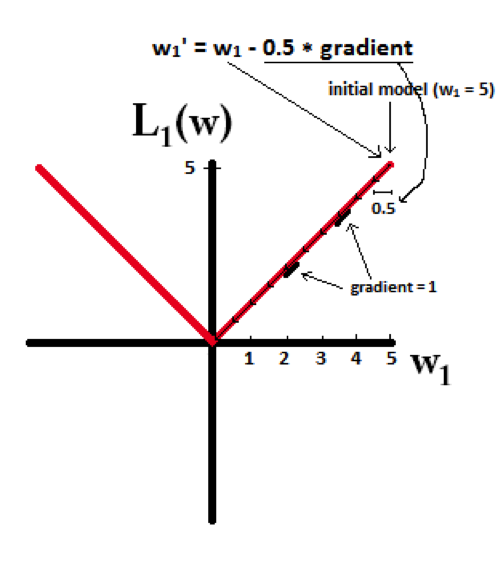
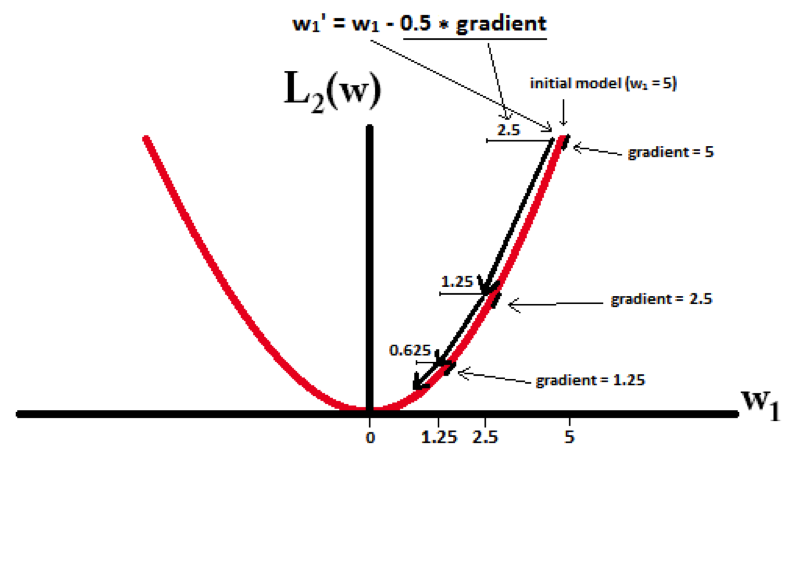
L1能产生等于0的权值，即能够剔除某些特征在模型中的作用（特征选择），即产生稀疏的效果。

L2可以得迅速得到比较小的权值，但是难以收敛到0，所以产生的不是稀疏而是平滑的效果。

角度二：几何空间

这个角度从几何位置关系来看权值的取值情况。

直接来看下面这张图：

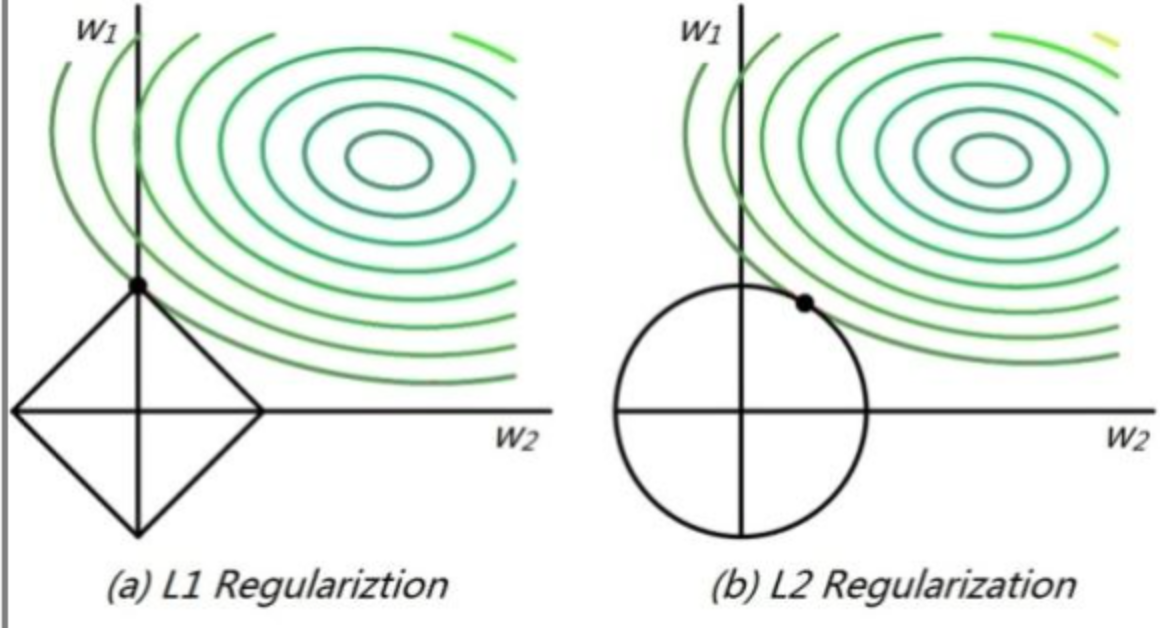
高维我们无法想象，简化到2维的情形，如上图所示。其中，左边是L1图示，右边是L2图示，左边的方形线上是L1中w1/w2取值区间，右边得圆形线上是L2中w1/w2的取值区间，绿色的圆圈表示w1/w2取不同值时整个正则化项的值的等高线（凸函数），从等高线和w1/w2取值区间的交点可以看到，L1中两个权值倾向于一个较大另一个为0，L2中两个权值倾向于均为非零的较小数。这也就是L1稀疏，L2平滑的效果。

文章地址: https://vimsky.com/article/969.html