时间复杂度 log n

时间复杂度 O(log n) 意味着什么？

预先知道算法的复杂度是一回事，了解其后的原理是另一件事情。

不管你是计算机科班出身还是想有效解决最优化问题，如果想要用自己的知识解决实际问题，你都必须理解时间复杂度。

先从简单直观的 O(1) 和 O(n) 复杂度说起。O(1) 表示一次操作即可直接取得目标元素（比如字典或哈希表），O(n) 意味着先要检查 n 个元素来搜索目标，但是 O(log n) 是什么意思呢？

你第一次听说 O(log n) 时间复杂度可能是在学二分搜索算法的时候。二分搜索一定有某种行为使其时间复杂度为 log n。我们来看看是二分搜索是如何实现的。

因为在最好情况下二分搜索的时间复杂度是 O(1)，最坏情况（平均情况）下 O(log n)，我们直接来看最坏情况下的例子。已知有 16 个元素的有序数组。

举个最坏情况的例子，比如我们要找的是数字 13。

十六个元素的有序数组

选中间的元素作为中心点（长度的一半）

13 小于中心点，所以不用考虑数组的后一半

重复这个过程，每次都寻找子数组的中间元素

每次和中间元素比较都会使搜索范围减半。

所以为了从 16 个元素中找到目标元素，我们需要把数组平均分割 4 次，也就是说，

简化后的公式

类似的，如果有 n 个元素，

归纳一下

分子和分母代入指数

等式两边同时乘以 2^k

最终结果

现在来看看「对数」的定义：

为使某数（底数）等于一给定数而必须取的乘幂的幂指数。

也就是说可以写成这种形式

对数形式

所以 log n 的确是有意义的，不是吗？没有其他什么可以表示这种行为。

就这样吧，我希望我讲得这些你都搞懂了。在从事计算机科学相关的工作时，了解这类知识总是有用的（而且很有趣）。说不定就因为你知道算法的原理，你成了小组里能找出问题的最优解的人呢，谁知道呢。祝好运！

• 原文地址：https://github.com/xitu/gold-miner/blob/master/TODO/what-does-the-time-complexity-o-log-n-actually-mean.md
• 原文作者：Maaz
• 译文出自：掘金翻译计划
• 译者：cdpath
• 校对者：zaraguo (zaraguo), whatbeg (Qiu Hu)

---

时间复杂度中的log（n）底数到底是多少？

其实这里的底数对于研究程序运行效率不重要，写代码时要考虑的是数据规模n对程序运行效率的影响，常数部分则忽略，同样的，如果不同时间复杂度的倍数关系为常数，那也可以近似认为两者为同一量级的时间复杂度。

现在来看看为什么底数具体为多少不重要？

读者只需要掌握（依稀记得）中学数学知识就够了。

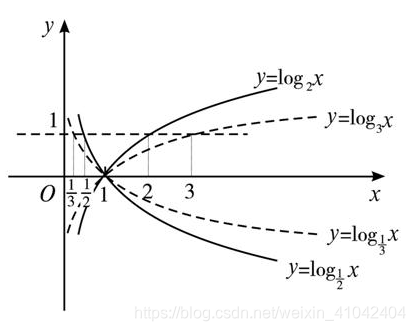
假设有底数为2和3的两个对数函数，如上图。当X取N（数据规模）时，求所对应的时间复杂度得比值，即对数函数对应的y值，用来衡量对数底数对时间复杂度的影响。

比值为log2 N / log3 N，运用换底公式后得：(lnN/ln2) / (lnN/ln3) = ln3 / ln2，ln为自然对数，显然这三个常数，与变量N无关。

用文字表述：算法时间复杂度为log（n）时，不同底数对应的时间复杂度的倍数关系为常数，不会随着底数的不同而不同，因此可以将不同底数的对数函数所代表的时间复杂度，当作是同一类复杂度处理，即抽象成一类问题。

当然这里的底数2和3可以用a和b替代，a，b大于等于2，属于整数。a,b取值是如何确定的呢？

有点编程经验的都知道，分而治之的概念。排序算法中有一个叫做“归并排序”或者“合并排序”的算法，它用到的就是分而治之的思想，而它的时间复杂度就是N*logN，此算法采用的是二分法，所以可以认为对应的对数函数底数为2，也有可能是三分法，底数为3，以此类推。

但是不可能是分数或者负数。

说明：为了便于说明，本文时间复杂度一概省略 O 符号。

版权声明：可转载，需要明确注明转载出处和链接；不允许商业用途。ttps://blog.csdn.net/bengxu/article/details/80320546