剑指Offer面试题:10.数值的整数次方
一、题目:数值的整数次方
题目:实现函数double Power(doublebase, int exponent),求base的exponent次方。不得使用库函数,同时不需要考虑大数问题。
在.NET Framework提供的BCL中,Math类实现了一个Pow方法,例如要求2的三次方,可以通过以下代码实现:
double result = Math.Pow(, );
本题就是要实现一个类似于该Pow方法的功能。
二、解决思路与实现
2.1 不加思索的思路
不需要考虑大数问题,可以在30秒内想到的思路如下:
public double Power(double baseNumber,int exponent)
{
double result = ;
for (int i = ; i <= exponent; i++)
{
result = result * baseNumber;
} return result;
}
但是,上面的代码没有考虑到输入的指数(exponent)小于1即是零和负数的时候怎么办,它只考虑了指数是正数的情况。
2.2 全面考虑的思路
(1)当指数为负数的时候:可以先对指数求绝对值,然后算出次方的结果之后再取倒数。
(2)当底数(base)是零且指数是负数的时候:通过全局代码或异常告诉调用者参数有误。
(3)0的0次方的时候:由于0的0次方在数学上是没有意义的,因此无论是输出0还是1都是可以接受的。
public static bool isInvalidInput = false;
public static double Power(double baseNumber, int exponent)
{
isInvalidInput = false;
// 当底数(base)是零且指数是负数的时候提示参数非法
if (Equals(baseNumber, 0.0) && exponent < )
{
isInvalidInput = true;
return 0.0;
}
uint absExponent = (uint)exponent;
if (exponent < )
{
absExponent = (uint)(- * exponent);
}
double result = PowerWithUintExponent(baseNumber, absExponent);
// 当指数为负数的时候需算出次方的结果之后再取倒数
if(exponent < )
{
result = 1.0 / result;
}
return result;
}
private static double PowerWithUintExponent(double baseNumber, uint exponent)
{
double result = 1.0;
for (int i = ; i <= exponent; i++)
{
result = result * baseNumber;
}
return result;
}
/// <summary>
/// 在判断底数base是不是等于0时,不能直接写base==0,
/// 这是因为在计算机内表示小数时(包括float和double型小数)都有误差。
/// </summary>
private static bool Equal(double num1, double num2)
{
if (num1 - num2 > -0.0000001 &&
num1 - num2 < 0.0000001)
{
return true;
}
else
{
return false;
}
}
细节:在判断底数baseNumber是不是等于0时,不能直接写baseNumber==0,这是因为在计算机内表示小数时(包括float和double型小数)都有误差。判断两个小数是否相等,只能判断它们之差的绝对值是不是在一个很小的范围内。如果两个数相差很小,就可以认为它们相等。
三、单元测试
3.1 测试用例
// 底数、指数都为正数
[TestMethod]
public void PowerTest1()
{
Assert.AreEqual(PowerHelper.Power(, ), );
} // 底数为负数、指数为正数
[TestMethod]
public void PowerTest2()
{
Assert.AreEqual(PowerHelper.Power(-, ), -);
} // 指数为负数
[TestMethod]
public void PowerTest3()
{
Assert.AreEqual(PowerHelper.Power(, -), 0.125);
} // 指数为0
[TestMethod]
public void PowerTest4()
{
Assert.AreEqual(PowerHelper.Power(, ), );
} // 底数、指数都为0
[TestMethod]
public void PowerTest5()
{
Assert.AreEqual(PowerHelper.Power(, ), );
} // 底数为0、指数为正数
[TestMethod]
public void PowerTest6()
{
Assert.AreEqual(PowerHelper.Power(, ), );
} // 底数为0、指数为负数
[TestMethod]
public void PowerTest7()
{
Assert.AreEqual(PowerHelper.Power(, -), );
Assert.AreEqual(PowerHelper.isInvalidInput, true);
}
3.2 测试结果
(1)测试通过结果

(2)代码覆盖率结果
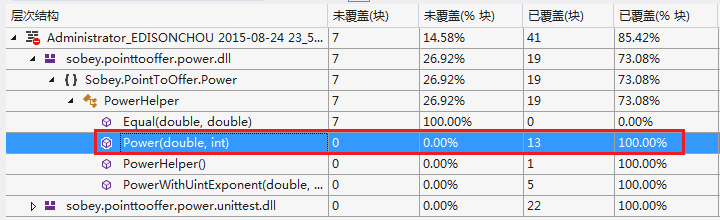
剑指Offer面试题:10.数值的整数次方的更多相关文章
- 剑指Offer:面试题11——数值的整数次方(java实现)
题目描述: 实现函数double Power(double base, int exponent),求base的exponent次方,不得使用库函数,同时不需要考虑大数问题 思路:本题的重点考察内容是 ...
- 剑指Offer - 九度1514 - 数值的整数次方
剑指Offer - 九度1514 - 数值的整数次方2013-11-30 00:49 题目描述: 给定一个double类型的浮点数base和int类型的整数exponent.求base的exponen ...
- 剑指offer_面试题11 数值的整数次方_考察代码的完整性
测试通过代码: package t0825; public class Power { public static void main(String[] args){ System.out.print ...
- 剑指offer十二之数值的整数次方
一.题目 给定一个double类型的浮点数base和int类型的整数exponent.求base的exponent次方. 二.思路 1.传统方法计算,时间复杂度O(n) 2.递归方式计算,时间复杂度O ...
- 剑指offer(12)数值的整数次方
题目描述 给定一个double类型的浮点数base和int类型的整数exponent.求base的exponent次方. 题目分析 这道题用传统的方法也可以做,只不过效率太低,这里我们用到快速幂的方法 ...
- 【剑指Offer】12、数值的整数次方
题目描述: 给定一个double类型的浮点数base和int类型的整数exponent.求base的exponent次方. 解题思路: 本题看似比较简单,是一个简单的指数运算,但需要完 ...
- 剑指offer 面试题43. 1~n整数中1出现的次数
leetcode上也见过一样的题,当时不会做 看了一下解法是纯数学解法就没看,结果剑指offer上也出现了这道题,那还是认真看下吧 对于数字abcde,如果第一位是1,比如12345,即计算f(123 ...
- 剑指offer——面试题10:斐波那契数列
个人答案: #include"iostream" #include"stdio.h" #include"string.h" using na ...
- 剑指Offer面试题10(Java版):二进制中的1的个数
题目:请实现一个函数,输入一个整数.输出该数二进制表示中1的个数. 比如把9表示成二进制是1001,有2位是1.因此假设输入9.该函数输出2. 1.可能引起死循环的解法 这是一道非常主要的考察二进制和 ...
- 剑指offer 面试题10.2:青蛙变态跳台阶
题目描述 一只青蛙一次可以跳上1级台阶,也可以跳上2级--它也可以跳上n级.求该青蛙跳上一个n级的台阶总共有多少种跳法. 编程思想 因为n级台阶,第一步有n种跳法:跳1级.跳2级.到跳n级跳1级,剩下 ...
随机推荐
- VirtualBox上搭建Ubuntu开发环境
软件版本: VirtualBox虚拟机:5.1.8 for Windows hosts x86/amd64 Ubuntu系统:Ubuntu 14.04.5 LTS Desktop (32-bit) ...
- [LeetCode] Best Time to Buy and Sell Stock II
Say you have an array for which the ith element is the price of a given stock on day i. Design an al ...
- ABP中单元测试的技巧:Mock和数据驱动
(此文章同时发表在本人微信公众号"dotNET每日精华文章",欢迎右边二维码来关注.) 题记:虽然ABP为大家提供了测试的脚手架了,不过有些小技巧还是需要自己探索的. ASP.NE ...
- 关于 Dictionary<string,string>,和List<T>在View的使用
在MVC中Dictionary<string,string>如何应用到View页面中呢,例: <input type="text" name=key value= ...
- UWP学习记录4-设计和UI之控件和模式1
UWP学习记录4-设计和UI之控件和模式1 1.控件和事件简介 在 UWP 应用开发中,控件是一种显示内容或支持交互的 UI 元素. 控件是用户界面的构建基块. 我们提供了超过 45 种控件供你使用, ...
- 4.View绘制分析笔记之onDraw
上一篇文章我们了解了View的onLayout,那么今天我们来学习Android View绘制三部曲的最后一步,onDraw,绘制. ViewRootImpl#performDraw private ...
- OX中修改文件名
右击文件,显示简介,名称与扩展名
- SSDB 主从配置
环境 Master/Slave 系统 IP SSDB版本 Master CentOS6.7 10.10.3.211 ssdb-1.8.0 Sla ...
- 使用display:table来解决一些问题
一直有,多栏的需求,当然用table布局,很快就做完了.不怎么喜欢用table,刚开始使用display:table,但是有一条老是不能达到我的效果,那就是有一行不固定宽度的时候,就不知道怎么处理,今 ...
- SQL Server 2008 表变量 临时表
最近做一个报表,其中 在报表中用到了存储过程,游标,cte表达式,临时表和表变量. 在游标中循环遍历cte中的数据,把对应的数据存放在变量里面,之后把变量插入到表变量中,游标结束后,想要根据存储过程的 ...
