HNOI2008玩具装箱斜率优化

题目描述

P教授要去看奥运，但是他舍不下他的玩具，于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩，其可以将任意物品变成一堆，再放到一种特殊的一维容器中。P教授有编号为1...N的N件玩具，第i件玩具经过压缩后变成一维长度为Ci.为了方便整理，P教授要求在一个一维容器中的玩具编号是连续的。同时如果一个一维容器中有多个玩具，那么两件玩具之间要加入一个单位长度的填充物，形式地说如果将第i件玩具到第j个玩具放到一个容器中，那么容器的长度将为 x=j-i+Sigma(Ck) i<=K<=j 制作容器的费用与容器的长度有关，根据教授研究，如果容器长度为x,其制作费用为(X-L)^2.其中L是一个常量。P教授不关心容器的数目，他可以制作出任意长度的容器，甚至超过L。但他希望费用最小.

输入格式：

第一行输入两个整数N，L.接下来N行输入Ci.1<=N<=50000,1<=L,Ci<=10^7

输出格式：

输出最小费用

首先，这道题我们可以把所有的玩具长度加1，让后让L加1，就不存在什么填充物之类的，从而将这个问题转化为：把一个序列分为若干段，使得（（每一段的和与常数L的差）的平方）相加起来的和最小。

那我们显而易见就先对这个序列求出每一个位置的前缀和，然后一个O(n^2)的dp就很明显了：

设f[i]表示恰好分完前i个数的最小代价，p[i]表示前i个数的和。

考虑转移：f[i]=min{ f[j]+(p[i]-p[j]-L)^2 }(0<=j<i)

然而，n<=50000，复杂度肯定会爆炸，所以我们需要优化这个dp，但是由于状态至少是线性的(反正我是想不出来)，因而我们只能优化转移。

从转移方程入手：

f[i]=min{ f[j]+((p[i]-L)-p[j])^2 }(0<=j<i)

=(p[i]-L)^2+min{ f[j] + p[j]^2 - 2*p[i]*p[j] + 2*L*p[j] }

=(p[i]-L)^2+min{ f[j] + p[j]^2 + 2*L*p[j] - 2*p[i]*p[j] }

对于每一个i，有p[i]是定值，我们可以在dp的时候顺便用t[i]储存f[i] + p[i]^2 + 2*L*p[i]。

所以这个式子又变成了

f[i]-(p[i]-L)^2=min{ t[j] - 2*p[i]*p[j] }（0<=j<i）

我们若想f[i]-(p[i]-L)^2最小，设f[i]-(p[i]-L)^2=b，f[i]从j转移，则有，t[j]=2*p[j]*p[i]+b。

这个式子特别像一次函数的解析式，这时我们又发现对于i，p[i]确定，而且p数组满足单调递增，我们就可以想象平面上有若干个点，第j个点坐标是(p[j],t[j])。而我们需要找到一条斜率确定为2*p[i]并且过这些点中某一个点的直线，使他的截距(即上文中提到的b)最小。由于p[i]单调递增，因此每个i所对应的斜率也是单调递增的，并且将第i个点加入后第i个点一定是最靠右的。

这时我们就可以用单调队列维护一个下凸壳，每次从队首的点转移，若队首的点不是最优的(不如队列中第二个点更优)，就把队首弹出，然后每次转移完f[i]时更新t[i]，并将i压入单调队列中。

注意初始时队中应该有一个点(0,0)。

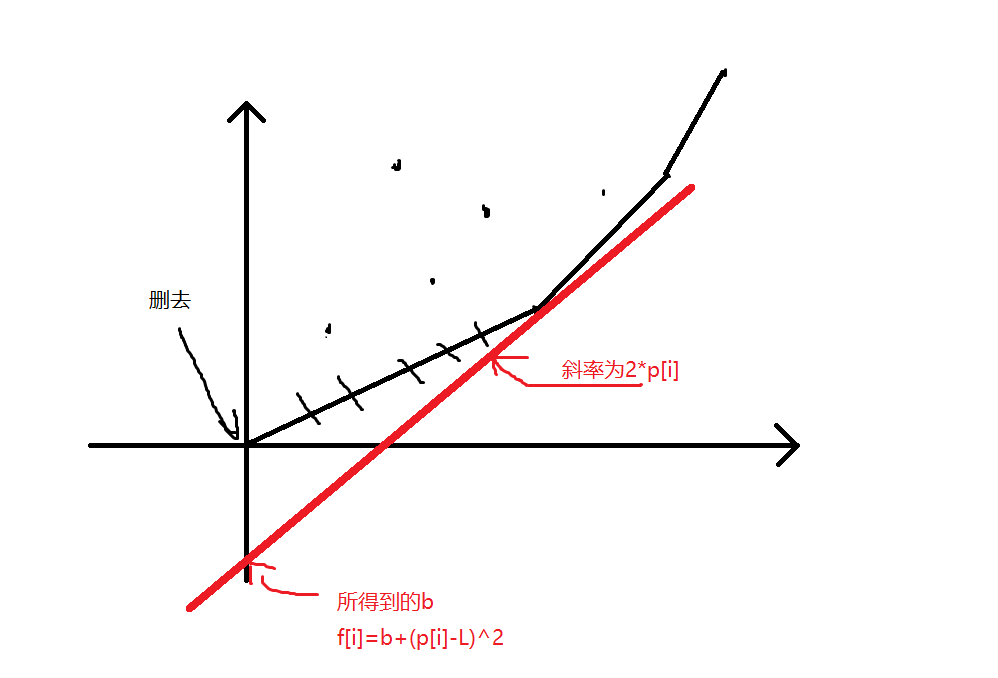
这个图有点抽象，图中的斜率远小于实际

AC代码如下

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LL long long
#define M 500020
using namespace std;
LL read(){
	LL nm=0ll,fh=1ll;char cw=getchar();
	for(;!isdigit(cw);cw=getchar()) if(cw=='-') fh=-fh;
	for(;isdigit(cw);cw=getchar()) nm=nm*10ll+(cw-'0');
	return nm*fh;
}
LL n,f[M],L,p[M],t[M],rem,now,cnt,q[M][2],hd,tl=1;
LL gt_ans(LL k,LL pos){LL y=q[pos][1],x=q[pos][0];return y-x*k*2;}
int main(){
	n=read(),L=read()+1;
	for(LL i=1;i<=n;i++){
		p[i]=p[i-1]+read()+1;
		while(gt_ans(p[i],hd)>=gt_ans(p[i],hd+1)&&hd+1<tl) hd++;
		f[i]=gt_ans(p[i],hd)+(p[i]-L)*(p[i]-L);
		t[i]=p[i]*p[i]+2*L*p[i]+f[i];
		while(hd+1<tl&&(t[i]-q[tl-1][1])*(q[tl-1][0]-q[tl-2][0])<=(q[tl-1][1]-q[tl-2][1])*(p[i]-q[tl-1][0])) tl--;
		q[tl][0]=p[i],q[tl++][1]=t[i];
	}
	printf("%lld\n",f[n]);
	return 0;
}