【视觉SLAM14讲】ch3课后题答案

1.验证旋转矩阵是正交矩阵

感觉下面这篇博客写的不错

http://www.cnblogs.com/caster99/p/4703033.html

总结一下：旋转矩阵是一个完美的矩阵——正交矩阵。①行列式为1，②每个列向量都是单位向量且相互正交，③它的逆等于它的转置。

---

2.罗德里格斯公式的简单推导

http://blog.sina.com.cn/s/blog_ea828d2a0102wlk6.html

罗德里格斯旋转公式是通过反对称矩阵求旋转矩阵的方法，起初我在看别人写的姿态解算分析文章里看到，他的推导如下：

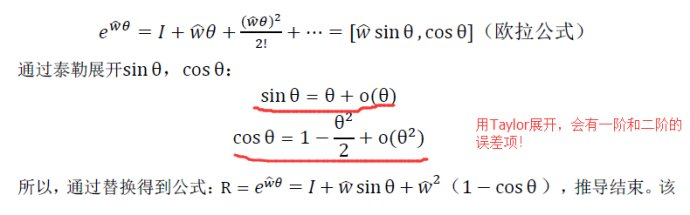
请注意我做标记的地方，我刚开始一直不明白这种推导，这样会有误差的推导，难道罗德里格斯公式是对旋转矩阵Ｒ的近似？这样做并不好，反而会使解算的姿态更不准确，后来在群里讨论这个问题，有大神给我解惑了。
首先我们明白这是一个SO(3)到SO(3)的李群的映射。不要担心自己不知道李群是什么，因为我们下面的推导会非常简单！

我们先来看什么是反对称矩阵，在这之前，先展示它和向量叉乘(内积)的关系：

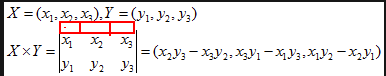
红色三个格子应该是i  j  k

下面看看我们的反对称矩阵运算：

加一个小三角，就是将这个向量变成一个反对称矩阵

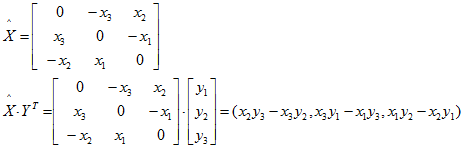
所以我们得出：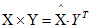

我们知道我们的旋转矩阵Ｒ和我们的三角函数的关系，这里就不多说了，所以现在我们来看一个反对称矩阵的性质，首先定义一个反对称矩阵：

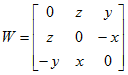
同时我们有如下的约束：

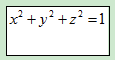
现在我们可以看到我们的反对称阵有如下性质：

现在可以进行我们的罗德里格斯公式推导了：

---

3. 验证四元数旋转某个点后，结果是一个虚四元数（实部为零），所以仍然对应 到一个三维空间点（式 3.34）。

=.=  看我干啥？下一题

---

4.旋转矩阵  轴角  欧拉角  四元数

书上都有

P42 轴角[n,α]与旋转矩阵的关系

P52 轴角[n,α]与四元数的关系

欧拉角存在gimbal lock，不研究他的关系【其实我不会】

---

5.假设有一个大的eigen矩阵，想把他的左上角的3*3取出来，然后赋值为I_3x3

---

6.Ax = b的Eigen实现

---

7.

机器人一号和二号，分别在世界坐标系中。 
一号的位姿q1=[0.35,0.2,0.3,0.1], t1=[0.3,0.1,0.1]T。 
二号的位姿q2=[−0.5,0.4,−0.1,0.2], t2=[−0.1,0.5,0.3]T。 
q的第一项是实部，且还未归一化。 
已知一号机器人看到某个点，在他的坐标系下是p=[0.5,0,0.2]T, 求在二号机器人坐标系下该点的位置。

#include <iostream>
#include <cmath>
 
// Eigen 部分
#include <Eigen/Core>
// 稠密矩阵的代数运算（逆，特征值等）
#include <Eigen/Dense>
//Eigen 几何模块
#include <Eigen/Geometry>
 
using namespace std;
 
int main(int argc, char **argv) {
    Eigen::Quaterniond q1(0.35, 0.2, 0.3, 0.1);
    Eigen::Quaterniond q2(-0.5, 0.4, -0.1, 0.2);
    Eigen::Vector3d t1(0.3, 0.1, 0.1);
    Eigen::Vector3d t2(-0.1, 0.5, 0.3);
    Eigen::Vector3d p1(0.5, , 0.2);
 
    Eigen::Quaterniond q1_one = q1.normalized();
    Eigen::Quaterniond q2_one = q2.normalized();
 
    //way1
 
    Eigen::Vector3d v = q1_one.inverse() * (p1 - t1);
    Eigen::Vector3d v2 = q2_one * v + t2;
    cout << "way1 v2 = " << endl << v2 << endl;
 
    //way2
    Eigen::Matrix3d R1 = Eigen::Matrix3d(q1_one);
    Eigen::Matrix3d R2 = Eigen::Matrix3d(q2_one);
    Eigen::Vector3d v_2 = R1.inverse() * (p1 - t1);
    Eigen::Vector3d v_2_2 = R2 * v_2 + t2;
    cout << "way2 v2= " << endl << v_2_2 << endl;
 
    return ;
}

way1 v2 =
-0.0309731
   0.73499
  0.296108
 
way2 v2=
-0.0309731
   0.73499
  0.296108
*** Exited normally ***