hihoCoder #1321 : 搜索五•数独（Dancing Links ,精确覆盖）

hiho一下第102周的题目。

原题地址：http://hihocoder.com/problemset/problem/1321

题意：输入一个9*9数独矩阵，0表示没填的空位，输出这个数独的答案。

提示已经讲解的很清楚了。稍微整理下思路。最后附AC代码。

一、Dancing Links解决精确覆盖问题。

1.精确覆盖问题

给定一个n行，m列的01矩阵。从中选择若干行使得每一列有且恰好只有一个1。

例如：

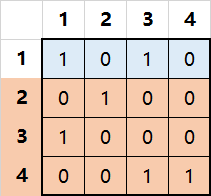
答案是选择2，3，4行。

2.DancingLinks求解精确覆盖问题

精确覆盖问题：从01矩阵中选择若干行使得每一列有且恰好只有一个1。

简单来说

精确覆盖问题的算法就是利用DFS搜索。

先选择一行，将当前覆盖的列以及能够覆盖到该列的所有行全部去掉，形成新的小规模的矩阵。

然后再逐行枚举，添加新的要覆盖的列，删除相应的行和列，重复直到剩下的矩阵只有1行。

如果剩下最后一行都是1，问题就解决了。

如果剩下最后一行还有0，则存在某些列没有被覆盖到。

DFS回溯求解。

而DancingLinks其实是一种数据结构。

不懂DangcingLinks的戳这里：http://www.cnblogs.com/grenet/p/3145800.html

DancingLinks模板（真不记得从哪里抄的）：

/*********************************************************************************

                      DLX模板 精确覆盖（exact_） 重复覆盖（repeat_）

**********************************************************************************/

struct DLX

{

    int n,m,SIZE;

    int U[maxnode],D[maxnode],R[maxnode],L[maxnode],Row[maxnode],Col[maxnode];//L,R,D,U四个数组记录某节点上下左右邻居

    int H[MaxN], S[MaxM];//H记录排头，S记录某列有多少个节点

    int ansd, ans[MaxN];

    void init(int _n,int _m)

    {

        n = _n;

        m = _m;

        for(int i = ;i <= m;i++)

        {

            S[i] = ;

            U[i] = D[i] = i;

            L[i] = i-;

            R[i] = i+;

        }

        R[m] = ; L[] = m;

        SIZE = m;

        for(int i = ;i <= n;i++)

            H[i] = -;

    }

    void Link(int r,int c)

    {

        ++S[Col[++SIZE]=c];

        Row[SIZE] = r;

        D[SIZE] = D[c];

        U[D[c]] = SIZE;

        U[SIZE] = c;

        D[c] = SIZE;

        if(H[r] < )H[r] = L[SIZE] = R[SIZE] = SIZE;

        else

        {

            R[SIZE] = R[H[r]];

            L[R[H[r]]] = SIZE;

            L[SIZE] = H[r];

            R[H[r]] = SIZE;

        }

    }

    void exact_Remove(int c)

    {

        L[R[c]] = L[c]; R[L[c]] = R[c];

        for(int i = D[c];i != c;i = D[i])

            for(int j = R[i];j != i;j = R[j])

            {

                U[D[j]] = U[j];

                D[U[j]] = D[j];

                --S[Col[j]];

            }

    }

    void repeat_remove(int c) {

    for(int i = D[c]; i != c; i = D[i])

        L[R[i]] = L[i], R[L[i]] = R[i];

    }

    void repeat_resume(int c) {

    for(int i = U[c]; i != c; i = U[i])

        L[R[i]] = R[L[i]] = i;

    }

    int f() { //估价函数。

    bool vv[MaxM];

    int ret = , c, i, j;

    for(c = R[]; c != ; c = R[c]) vv[c] = ;

    for(c = R[]; c != ; c = R[c])

        if(vv[c]) {

            ++ret, vv[c] = ;

            for(i = D[c]; i != c; i = D[i])

                for(j = R[i]; j != i; j = R[j])

                    vv[Col[j]] = ;

        }

    return ret;

    }

    void repeat_dance(int d) {

    if(d + f() >= ansd) return; //估价函数剪枝，A*搜索

    if(R[] == ) {

        if(d < ansd) ansd = d;

        return;

    }

    int c = R[], i, j;

    for(i = R[]; i; i = R[i])

        if(S[i] < S[c]) c = i;

    for(i = D[c]; i != c; i = D[i]) {

        repeat_remove(i);

        for(j = R[i]; j != i; j = R[j]) repeat_remove(j);

        repeat_dance(d + );

        for(j = L[i]; j != i; j = L[j]) repeat_resume(j);

        repeat_resume(i);

    }

}

    void exact_resume(int c)

    {

        for(int i = U[c];i != c;i = U[i])

            for(int j = L[i];j != i;j = L[j])

                ++S[Col[U[D[j]]=D[U[j]]=j]];

        L[R[c]] = R[L[c]] = c;

    }

    //d为递归深度

    bool exact_Dance(int d)

    {

        if(R[] == )

        {

            ansd = d;

            return true;

        }

        int c = R[];

        for(int i = R[];i != ;i = R[i])

            if(S[i] < S[c])

                c = i;

        exact_Remove(c);

        for(int i = D[c];i != c;i = D[i])

        {

            ans[d] = Row[i];

            for(int j = R[i]; j != i;j = R[j]) exact_Remove(Col[j]);

            if(exact_Dance(d+))return true;

            for(int j = L[i]; j != i;j = L[j]) exact_resume(Col[j]);

        }

        exact_resume(c);

        return false;

    }

};

/***********************************************************************************

                               模板结束

***********************************************************************************/

二、把一个数独问题转化为精确覆盖问题。

1.数独问题

给定一个9x9的矩阵。将1~9填入当中。其中有些格子已经填好了，有些格子则需要你填进去。

　　　　　对于填好后的矩阵，需要满足3个条件：

1. 　　每一个数字在每一行只能出现1次
2. 　　每一个数字在每一列只能出现1次
3. 　　每一个数字在每一个九宫区域内只能出现1次。

例如：

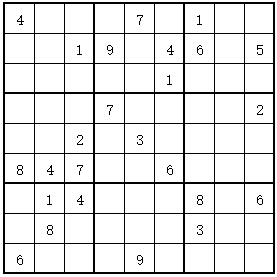
输入格式：数独9*9矩阵，0表示该格未填写数字，1~9表示该格已经填写有该数字。

样例输入：

4 0 0 0 7 0 1 0 0

0 0 1 9 0 4 6 0 5

0 0 0 0 0 1 0 0 0

0 0 0 7 0 0 0 0 2

0 0 2 0 3 0 0 0 0

8 4 7 0 0 6 0 0 0

0 1 4 0 0 0 8 0 6

0 2 0 0 0 0 3 0 0

6 0 0 0 9 0 0 0 0

2.如何把数独问题表示为精确覆盖问题

即把数独矩阵转化为01覆盖矩阵。

对于精确覆盖问题的01矩阵，其行与列的意义：

- - 　　列：一个原问题的约束条件
  - 　　行：一个方案所满足的约束条件

精确覆盖的结果选取若干个方案，每个方案可以满足一个或多个约束条件，每个条件恰被其中一个方案满足。

考虑数独问题的约束条件和方案。

约束条件：

1.每一个数字在每一行出现。

由于行和数字的互相匹配，因此一共会产生9x9，81个约束条件。

1. 第1行存在数字1

2. 第1行存在数字2

3. 第1行存在数字3
...

9. 第1行存在数字9

10. 第2行存在数字1

11. 第2行存在数字2
...

18. 第2行存在数字9

19. 第3行存在数字1
...

80. 第9行存在数字8

81. 第9行存在数字9

对于第 i 行第 j 列填写数字 k 时，其对应的列序号为 (i-1)*9+k

2.每一个数字在每一列出现。

由于列和数字的互相匹配，因此一共会产生9x9，81个约束条件：

第 i 列存在数字 j。（i=1~9， j=1~9）

对于第 i 行第 j 列填写数字 k 时，其对应的列序号为 81+(j-1)*9+k

3.每一个数字在每一个九宫出现。

由于九宫和数字的互相匹配，因此一共会产生9x9，81个约束条件：

第 i 个九宫格存在数字 j。（i=1~9， j=1~9）

对于第 i 行第 j 列填写数字 k 时，位于第t个九宫，其对应的约束条件序号为 162+(t-1)*9+k，

其中 t = ((i - 1) / 3 * 3 + (j - 1) / 3) + 1;

4.每一个格子填了一个数字

由于格子和数字的互相匹配，因此一共会产生9x9，81个约束条件：

格子（i，j）填了数字。

对于第 i 行第 j 列填写数字 k 时，其对应的约束条件序号为243+(i-1)*9+j

合计9*9*4=324个约束条件，对应的01矩阵有324列。

方案：

每一个格子可能填1-9这 9 个数字，一共有81个格子，总共是729个方案。

方案 “第 i 行第 j 列填写数字 k” 对应的行序号(方案编号)为 (（（i-1)*9+j）-1）*9+k

合计9*9*9=729个方案，对应的01矩阵有729行。

由此，9*9的数独问题转化为729*324的01矩阵的精确覆盖的问题。

转化成01矩阵的代码：

 char s[][]; //原数独矩阵

void setmx(int i,int  j,int k){   //方案“第i行第j列填写数字k”

    int id = (i - ) *  + j ;// 表示第i行第j列格子的编号

    int pid = (id - ) *  + k; // 表示该格子填写k所对应的方案编号

    // 约束条件1 - 对应第1~81列

    // 第(i-1)*9+k列表示第i行存在数字k

    dlx.Link(pid,(i - ) *  + k); //01矩阵(pid,(i - 1) * 9 + k)置1

    // 约束条件2 - 对应第82~162列

    // 第81+(j-1)*9+k列表示第j列存在数字k

dlx.Link(pid, + (j - ) *  + k); //01矩阵(pid,81 + (j - 1) * 9 + k)置1

    // 约束条件3 - 对应第163~243列

    // 第162+(t-1)*9+k列表示第t个九宫存在数字k

    int t = ((i - ) /  *  + (j - ) / ) + ;

dlx.Link(pid, + (t - ) *  + k);  //01矩阵(pid,162 + (t - 1) * 9 + k)置1

    // 约束条件4 - 对应第244~324列

    // 第243+id列表示第i行第j列填写有数字

    dlx.Link(pid, + id); //01矩阵(pid,243 + id)置1

}

void set_board()  //把原数独转化成729*324的01矩阵

{

    int i,j,k;

        for(i = ; i <= ; i++){

            for(j = ; j <= ; j++){

                if(s[i][j] == ''){ //位置(i,j)值不确定，可以为1~9

                    for(k = ; k <= ; k++){ //枚举可能的数字

                          setmx(i,j,k);

                    }

                }

                else{ //位置(i,j)值确定为k

                    k = s[i][j] - '';

                    setmx(i,j,k);

                }

            }

        }

}

3.由精确覆盖问题答案得到原数独问题的答案

精确覆盖的结果 选取若干个方案，每个方案可以满足一个或多个约束条件，每个条件恰被其中一个方案满足。

对应数独矩阵的意义

每个条件恰被其中一个方案满足：

约束条件1 “第1行存在数字1” 恰被一个方案满足，即“第一行存在且仅存在一个数字1”。

约束条件2 “第1行存在数字2” 恰被一个方案满足，即“第一行存在且仅存在一个数字2”。

……

约束条件324 “格子（9，9）填了数字” 恰被一个方案满足，即“格子（9，9）填了并仅填了一个数字”。

729*324的01矩阵的精确覆盖 满足了9*9的数独填完的所有约束条件。

而选取若干个方案：

方案一 “第 i1 行第 j1 列填写数字 k1”

方案二 “第 i2 行第 j2 列填写数字 k2”

……

选取的所有方案就是数独的答案。

对于每个方案, 第 i 行第 j 列填写数字 k

全部方案填入数独矩阵即为数独的答案。

精确覆盖答案还原成数独答案：

选取的方案即 01矩阵选择的行，利用DangcingLinks求解。

数组ans[]记录 01矩阵选取的行序号，ansd表示选择的行总数。

行序号 pid = (((i - 1) * 9 + j)-1)+k，得到行序号 pid 即可还原（i，j, k）的值，即得到方案 “第 i 行第 j 列填写数字 k”。

#1321 AC代码：

#include <algorithm>

#include <cstring>

#include <string.h>

#include <iostream>

#include <list>

#include <map>

#include <set>

#include <stack>

#include <string>

#include <utility>

#include <queue>

#include <vector>

#include <cstdio>

#include <cmath>

#define LL long long

using namespace std;

/************************************************************************************

                      DLX模板 精确覆盖（exact_） 重复覆盖（repeat_）

************************************************************************************/

const int maxnode = +;

const int MaxM = +;  //01矩阵列数

const int MaxN = +;  //01矩阵行数

struct DLX

{

    int n,m,SIZE;

    int U[maxnode],D[maxnode],R[maxnode],L[maxnode],Row[maxnode],Col[maxnode];//L,R,D,U四个数组记录某节点上下左右邻居

    int H[MaxN], S[MaxM];//H记录排头，S记录某列有多少个节点

    int ansd, ans[MaxN];

    void init(int _n,int _m)

    {

        n = _n;

        m = _m;

        for(int i = ;i <= m;i++)

        {

            S[i] = ;

            U[i] = D[i] = i;

            L[i] = i-;

            R[i] = i+;

        }

        R[m] = ; L[] = m;

        SIZE = m;

        for(int i = ;i <= n;i++)

            H[i] = -;

    }

    void Link(int r,int c)

    {

        ++S[Col[++SIZE]=c];

        Row[SIZE] = r;

        D[SIZE] = D[c];

        U[D[c]] = SIZE;

        U[SIZE] = c;

        D[c] = SIZE;

        if(H[r] < )H[r] = L[SIZE] = R[SIZE] = SIZE;

        else

        {

            R[SIZE] = R[H[r]];

            L[R[H[r]]] = SIZE;

            L[SIZE] = H[r];

            R[H[r]] = SIZE;

        }

    }

    void exact_Remove(int c)

    {

        L[R[c]] = L[c]; R[L[c]] = R[c];

        for(int i = D[c];i != c;i = D[i])

            for(int j = R[i];j != i;j = R[j])

            {

                U[D[j]] = U[j];

                D[U[j]] = D[j];

                --S[Col[j]];

            }

    }

    void repeat_remove(int c) {

    for(int i = D[c]; i != c; i = D[i])

        L[R[i]] = L[i], R[L[i]] = R[i];

    }

    void repeat_resume(int c) {

    for(int i = U[c]; i != c; i = U[i])

        L[R[i]] = R[L[i]] = i;

    }

    int f() { //估价函数。

    bool vv[MaxM];

    int ret = , c, i, j;

    for(c = R[]; c != ; c = R[c]) vv[c] = ;

    for(c = R[]; c != ; c = R[c])

        if(vv[c]) {

            ++ret, vv[c] = ;

            for(i = D[c]; i != c; i = D[i])

                for(j = R[i]; j != i; j = R[j])

                    vv[Col[j]] = ;

        }

    return ret;

    }

    void repeat_dance(int d) {

    if(d + f() >= ansd) return; //估价函数剪枝，A*搜索

    if(R[] == ) {

        if(d < ansd) ansd = d;

        return;

    }

    int c = R[], i, j;

    for(i = R[]; i; i = R[i])

        if(S[i] < S[c]) c = i;

    for(i = D[c]; i != c; i = D[i]) {

        repeat_remove(i);

        for(j = R[i]; j != i; j = R[j]) repeat_remove(j);

        repeat_dance(d + );

        for(j = L[i]; j != i; j = L[j]) repeat_resume(j);

        repeat_resume(i);

    }

}

    void exact_resume(int c)

    {

        for(int i = U[c];i != c;i = U[i])

            for(int j = L[i];j != i;j = L[j])

                ++S[Col[U[D[j]]=D[U[j]]=j]];

        L[R[c]] = R[L[c]] = c;

    }

    //d为递归深度

    bool exact_Dance(int d)

    {

        if(R[] == )

        {

            ansd = d;

            return true;

        }

        int c = R[];

        for(int i = R[];i != ;i = R[i])

            if(S[i] < S[c])

                c = i;

        exact_Remove(c);

        for(int i = D[c];i != c;i = D[i])

        {

            ans[d] = Row[i];

            for(int j = R[i]; j != i;j = R[j]) exact_Remove(Col[j]);

            if(exact_Dance(d+))return true;

            for(int j = L[i]; j != i;j = L[j]) exact_resume(Col[j]);

        }

        exact_resume(c);

        return false;

    }

};

/***********************************************************************************

                      模板结束

**********************************************************************************/


DLX dlx;

 char s[][]; //原数独矩阵

void setmx(int i,int  j,int k){

    int id = (i - ) *  + j ;// 表示第i行第j列格子的编号

    int pid = (id - ) *  + k; // 表示该格子填写k所对应的方案编号

    // 约束条件1 - 对应第1~81列

    // 第(i-1)*9+k列表示第i行存在数字k

    dlx.Link(pid,(i - ) *  + k);

    // 约束条件2 - 对应第82~162列

    // 第81+(j-1)*9+k列表示第j列存在数字k

        dlx.Link(pid, + (j - ) *  + k);

    // 约束条件3 - 对应第163~243列

    // 第162+(t-1)*9+k列表示第t个九宫存在数字k

    int t = ((i - ) /  *  + (j - ) / ) + ;

        dlx.Link(pid, + (t - ) *  + k);

    // 约束条件4 - 对应第244~324列

    // 第243+id列表示第i行第j列填写有数字

    dlx.Link(pid, + id);

}

void set_board() //把原数独矩阵转化成729*324的01矩阵

{

    int i,j,k;

        for(i = ; i <= ; i++){

            for(j = ; j <= ; j++){

                if(s[i][j] == ''){ //位置(i,j)值不确定，可以为1~9

                    for(k = ; k <= ; k++){

                          setmx(i,j,k);

                    }

                }

                else{ //位置(i,j)值确定为k

                    k = s[i][j] - '';

                    setmx(i,j,k);

                }

            }

        }

}

int ans[][]; //数独答案

void print()  //精确覆盖答案还原成数独答案

{

    int i,j,k;

    for(int id=;id<dlx.ansd;id++)

        {

            int a=dlx.ans[id];  //ans[]存的是精确覆盖行号

            //行号 pid = (((i - 1) * 9 + j)-1)+k;

            //由此可以还原i,j,k的值

            //即得到信息，第i行第j列位置值为k

            //注意i,j,k取值范围均为1~9

            k=a%; if(k==) k=; //得到k

            a-=k; a/=; a+=;

            j=a%; if(j==) j=; //得到 j

            a-=j; a/=; a+=;

            i=a%; if(i==) i=; //得到 i

            ans[i][j]=k;  //方案 第 i 行第 j 列填写数字 k

        }

 //输出数独答案

    for(i=;i<=;i++)

    for(j=;j<=;j++)

        {

            if(j!=) cout<<ans[i][j]<<' ';

    else cout<<ans[i][j]<<endl;

        }

}

int main()

{

    int T;

    int n,m;

    scanf("%d",&T);

    while(T--)

    {

        for(int i = ; i <= ; i++)

            for(int j = ; j <= ; j++)

            scanf(" %c",&s[i][j]);      //输入原数独矩阵

          //9*9的数独问题转化为729*324的01矩阵的精确覆盖

        n = ;                         //729个方案。对应01矩阵有729行。

        m = ;                        //324个约束条件，对应的01矩阵有324列

        dlx.init(n,m);

        set_board();                    //数独矩阵转化为729*324的01矩阵

        dlx.exact_Dance();         //DLX求解精确覆盖

        print();                            //输出数独答案

    }

    return ;

}

hihoCoder #1321 : 搜索五•数独（Dancing Links ,精确覆盖）的更多相关文章

【转】Dancing Links精确覆盖问题
原文链接:http://sqybi.com/works/dlxcn/ (只转载过来一部分,全文请看原文,感觉讲得很好~)正文精确覆盖问题解决精确覆盖问题舞蹈步骤效率分析 ...
ZOJ 3209 Treasure Map （Dancing Links 精确覆盖）
题意 : 给你一个大小为 n * m 的矩形 , 坐标是( 0 , 0 ) ~ ( n , m ) .然后给你 p 个小矩形 . 坐标是( x1 , y1 ) ~ ( x2 , y2 ) , 你选 ...
hust 1017 dancing links 精确覆盖模板题
最基础的dancing links的精确覆盖题目 #include <iostream> #include <cstring> #include <cstdio> ...
HDU 3111 Sudoku ( Dancing Links 精确覆盖模型 )
推荐两篇学DLX的博文: http://bbs.9ria.com/thread-130295-1-1.html(这篇对DLX的工作过程演示的很详细) http://yzmduncan.iteye.co ...
POJ3074 Sudoku —— Dancing Links 精确覆盖
题目链接:http://poj.org/problem?id=3074 Sudoku Time Limit: 1000MS Memory Limit: 65536K Total Submissio ...
HUST1017 Exact cover —— Dancing Links 精确覆盖模板题
题目链接:https://vjudge.net/problem/HUST-1017 1017 - Exact cover 时间限制:15秒内存限制:128兆自定评测 7673 次提交 3898 次 ...
HDU5046 Airport dancing links 重复覆盖+二分
这一道题和HDU2295是一样是一个dancing links重复覆盖解决最小支配集的问题在给定长度下求一个最小支配集,只要小于k就行然后就是二分答案,每次求最小支配集只不过HDU2295是浮 ...
166. 数独 dancing links 方法
dfs硬怼通过数独 N皇后的代码后想学习下新的数据结构和算法来解决这类覆盖问题习题练习 https://www.acwing.com/problem/content/168/ 数独 https:/ ...
hdu 1426 Sudoku Killer ( Dancing Link 精确覆盖 )
利用 Dancing Link 来解数独详细的能够看 lrj 的训练指南和 < Dancing Links 在搜索中的应用 >这篇论文 Dancing Link 来求解数独 , ...

随机推荐

XCTest(二)
New tool sets are making it easier and easier to engage in genuine agile development on iOS. In part ...
python定时执行方法
1 time.sleep import time for i in range(5): print(i) time.sleep(10) 2 用shed import time import sche ...
python 常用的模块(hashlib)转
摘要算法简介 Python的hashlib提供了常见的摘要算法,如MD5,SHA1等等. 什么是摘要算法呢?摘要算法又称哈希算法.散列算法.它通过一个函数,把任意长度的数据转换为一个长度固定的数据串( ...
Spring随笔之ApplicationContext
前言以前自己学习和实习的时候多次用过spring框架.对于我这种菜鸟来说,Spring给我的第一印象是好学,太TM好学了(抱歉没忍住脏话),跟着开发组熟悉几天就可以开始写代码,自我感觉代码敲得飞起~ ...
HDFS删除并清空回收站
删除文件并放入回收站: hdfs dfs -rm -f /path 删除文件不放入回收站: hdfs dfs -rm -f -skipTrash /path 清空回收站: hdfs dfs -expu ...
Java高级特性—并发包
1). java并发包介绍 JDK5.0 以后的版本都引入了高级并发特性,大多数的特性在java.util.concurrent 包中,是专门用于多线程发编程的, 主要包含原子量.并发集合.同步器.可 ...
asp.net敏感词过滤
敏感词过滤是一个能够让用户发表评论的网站的一个很重要的功能(你懂的~) 下面开始全套流程: 1.需要有一套比较完整的词库,由于我的词库很少所以就不贴上来了,网上找找应该很多 2.设计一个可以将词库导入 ...
spring自动装配（No qualifying bean ）
No qualifying bean of type [com.wfj.service.cms.main.ChannelMng] found for dependency: expected at l ...
OpenCV2学习笔记（十五）：利用Cmake高速查找OpenCV函数源代码
在使用OpenCV时,在对一个函数的调用不是非常了解的情况下,通常希望查到该函数的官方声明.而假设想进一步研究OpenCV的函数,则必须深入到源码. 在VS中我们能够选中想要查看的OpenCV函数,点 ...
【Django】01_创建一个简单的项目
1.创建Django项目点击:file-->new project,出现下面的对话框.选择Django栏目,输入项目名称, 选择python解释器版本,点击create创建. Django将自 ...

hihoCoder #1321 : 搜索五•数独 （Dancing Links ,精确覆盖）

hihoCoder #1321 : 搜索五•数独 （Dancing Links ,精确覆盖）的更多相关文章

随机推荐

热门专题

hihoCoder #1321 : 搜索五•数独（Dancing Links ,精确覆盖）

hihoCoder #1321 : 搜索五•数独（Dancing Links ,精确覆盖）的更多相关文章