LDA与最小二乘法的关系及其变种详解

1 LDA与最小二乘法的关联

对于二值分类问题，令人惊奇的是最小二乘法和LDA分析是一致的。回顾之前的线性回归，给定N个d维特征的训练样例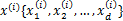（i从1到N），每个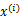对应一个类标签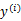。我们之前令y=0表示一类，y=1表示另一类，现在我们为了证明最小二乘法和LDA的关系，改变训练目标：

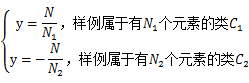
就是将训练目标0/1做了值替换。我们列出最小二乘法代价函数：

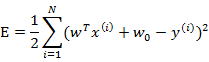
w和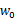是拟合权重参数。分别对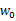和w求导得：

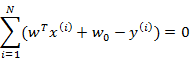
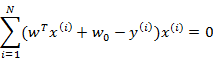
从第一个式子展开可以得到：

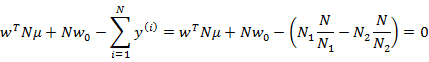
消元后，得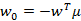。又因为：

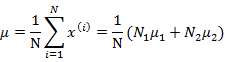
化简第二个求导式子展开后和下面的公式等价：

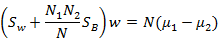
其中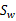和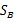是二值分类中类内离散矩阵和类间离散矩阵。由于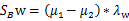

因此，最后结果仍然是：

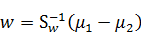
这个过程从几何意义上去理解也就是变形后的线性回归（将类标签重新定义），线性回归后的直线方向就是二值分类中LDA求得的直线方向w。

2.LDA的变种详解