P3389 【模板】高斯消元法

高斯消元求解n元一次线性方程组的板子题：

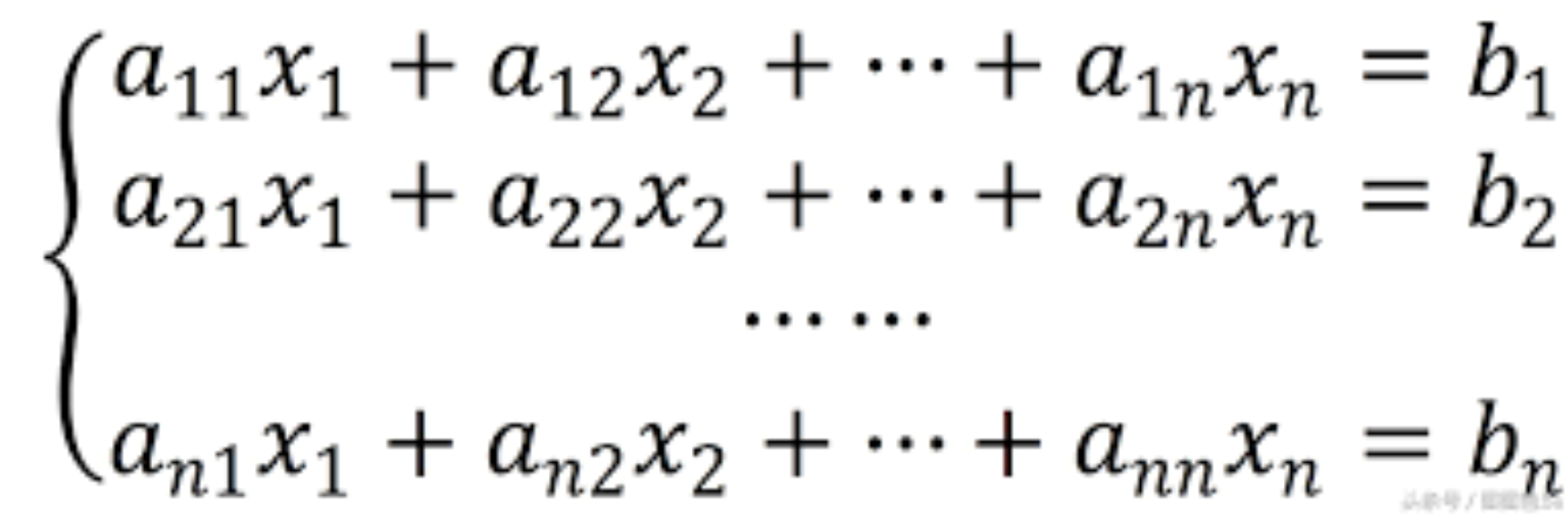
先举个栗子：

• 2x + y -   z =  8-----------①

•-3x - y + 2z = -11---------②

•-2x + y + 2z = -3----------③

 先将它存到矩阵中：

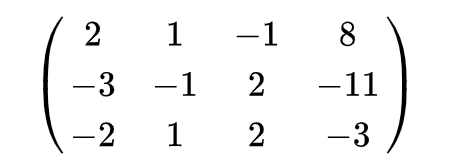
②+①* (2/3)

③+①

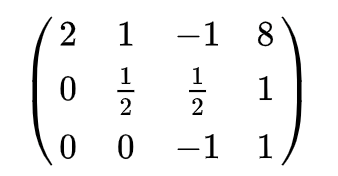
接着对①变换

得到x，y，z；

但是我们想到，如果它有在原方程中就有两个或多个方程本质上是一样的，那他不就解不出来了咩？

比如：

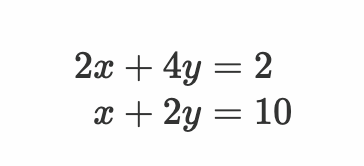
最后得出：

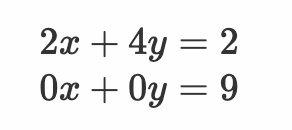
这显然就属于无解的情况

又比如：

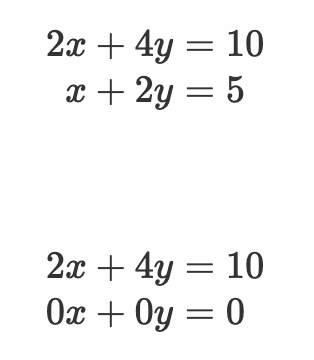
这显然就属于无穷多解的情况

这里我们引入一个定理：

一个矩阵的行列式如果不为0，方程组有唯一解，否则无解或者无穷多解

然后我们就可以通过计算行列式来判断有无解辣！

---

高斯消元求解线性方程组的步骤：

Step1:利用高斯消元将原矩阵（蒟阵 变为对角矩阵    

 　　具体方法：将a[i][i]除成1，这一行也进行同样的变换，用这个1去消其他的项

Step2:将对角线上的值连乘得到行列式

　　　　一个矩阵的行列式如果不为0，方程组有唯一解，否则无解或者无穷多解

 

在将原矩阵变为对角矩阵的过程中，线性方程组就已经消成了ax=b的形式，故只需要判断有无解即可；

求行列式：

先了解一下运算法则：传送门

行列式的计算：

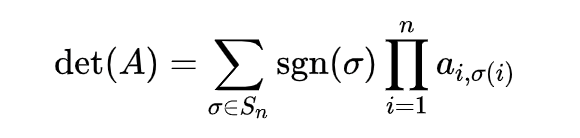
举两个例子

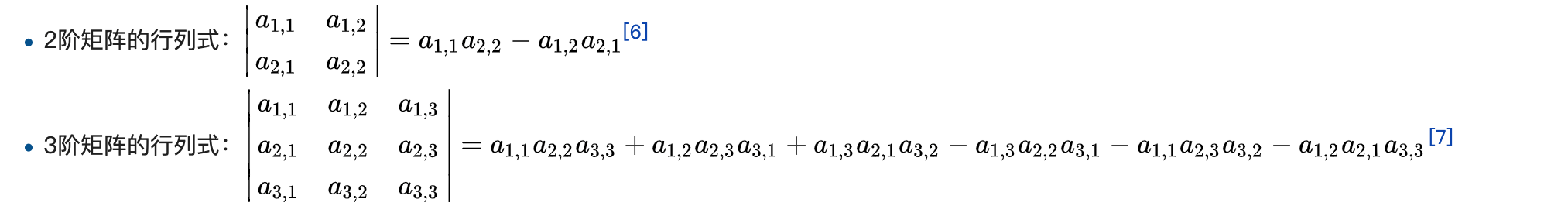
测试代码如下（注意是这里输入n是未知数个数，m是方程个数,对于这个题mn输入一样的就可以辣！）：

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<cstdlib>
 using namespace std;
 typedef long long ll;
 typedef long double ld;
 typedef pair<int,int> pr;
 const double pi=acos(-);
 #define rep(i,a,n) for(int i=a;i<=n;i++)
 #define per(i,n,a) for(int i=n;i>=a;i--)
 #define Rep(i,u) for(int i=head[u];i;i=Next[i])
 #define clr(a) memset(a,0,sizeof a)
 #define pb push_back
 #define mp make_pair
 #define fi first
 #define sc second
 ld eps=1e-;
 ll pp=;
 ll mo(ll a,ll pp){if(a>= && a<pp)return a;a%=pp;if(a<)a+=pp;return a;}
 ll powmod(ll a,ll b,ll pp){ll ans=;for(;b;b>>=,a=mo(a*a,pp))if(b&)ans=mo(ans*a,pp);return ans;}
 ll read(){
     ll ans=;
     char last=' ',ch=getchar();
     while(ch<'' || ch>'')last=ch,ch=getchar();
     while(ch>='' && ch<='')ans=ans*+ch-'',ch=getchar();
     if(last=='-')ans=-ans;
     return ans;
 }
 //head
 int n,m;
 double a[][];

 bool check(int k){
     if(fabs(a[k][n+])<eps)return ;
     rep(i,,n)
         if(fabs(a[k][i])>eps)return ;
     return ;
 }
 int main(){

     n=read();m=read();
     // a_i,1 a_i,2 ... a_i,n a_i,n+1
     rep(i,,m)
         rep(j,,n+)a[i][j]=read();
     rep(j,,m){
             rep(k,,n+)cout<<a[j][k]<<" ";
             puts("");
         }
     int flag=;
     rep(i,,n){
         int t=i;
         while(a[t][i]== && t<=n)t+=;
         if(t==n+){
             flag=;
             continue;
         }
         rep(j,,n+)swap(a[i][j],a[t][j]);//交换两行
         double kk=a[i][i];//每一行对角线上的值
         rep(j,,n+)a[i][j]/=kk;
         rep(j,,m)//循环m个式子 开始消元
             if(i!=j){
                 double kk=a[j][i];
                 rep(k,,n+)
                     a[j][k]-=kk*a[i][k];//这样就能保证正好把第i列的数除了a[i][i] 都消成0
             }
         puts("------------");
         rep(j,,m){
             rep(k,,n+)cout<<a[j][k]<<" ";
             puts("");
         }
     }
     if(flag){//如果flag=1，可能是 无解，也可能是无穷解
         rep(i,,m)
             if(!check(i)){
                 printf("No solution\n");
                 return ;
             }
         printf("So many solutions\n");
     }

 }

本题AC代码：稍微改一下就行啦

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int,int> pr;
const double pi=acos(-);
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,n,a) for(int i=n;i>=a;i--)
#define Rep(i,u) for(int i=head[u];i;i=Next[i])
#define clr(a) memset(a,0,sizeof a)
#define pb push_back
#define mp make_pair
#define fi first
#define sc second
ld eps=1e-;
ll pp=;
ll mo(ll a,ll pp){if(a>= && a<pp)return a;a%=pp;if(a<)a+=pp;return a;}
ll powmod(ll a,ll b,ll pp){ll ans=;for(;b;b>>=,a=mo(a*a,pp))if(b&)ans=mo(ans*a,pp);return ans;}
ll read(){
    ll ans=;
    char last=' ',ch=getchar();
    while(ch<'' || ch>'')last=ch,ch=getchar();
    while(ch>='' && ch<='')ans=ans*+ch-'',ch=getchar();
    if(last=='-')ans=-ans;
    return ans;
}
//head
int n,m;
double a[][];

bool check(int k){
    if(fabs(a[k][n+])<eps)return ;
    rep(i,,n)
        if(fabs(a[k][i])>eps)return ;
    return ;
}
int main(){

    n=read();m=n;
    // a_i,1 a_i,2 ... a_i,n a_i,n+1
    rep(i,,m)
        rep(j,,n+)a[i][j]=read();

    int flag=;
    rep(i,,n){
        int t=i;
        while(a[t][i]== && t<=n)t+=;
        if(t==n+){
            flag=;
            continue;
        }
        rep(j,,n+)swap(a[i][j],a[t][j]);//交换两行
        double kk=a[i][i];//每一行对角线上的值
        rep(j,,n+)a[i][j]/=kk;
        rep(j,,m)//循环m个式子 开始消元
            if(i!=j){
                double kk=a[j][i];
                rep(k,,n+)
                    a[j][k]-=kk*a[i][k];//这样就能保证正好把第i列的数除了a[i][i] 都消成0
            }
    }
    if(flag){

        return printf("No Solution\n"),;
    }
    rep(j,,m){
            printf("%.2lf",a[j][n+]/a[j][j]);
            puts("");
        }

}